Fourier transform in MATLAB
Last Updated :
30 May, 2021
Fourier Transform is a mathematical technique that helps to transform Time Domain function x(t) to Frequency Domain function X(ω). In this article, we will see how to find Fourier Transform in MATLAB.
The mathematical expression for Fourier transform is: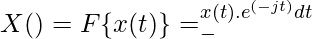
Using the above function one can generate a Fourier Transform of any expression. In MATLAB, the Fourier command returns the Fourier transform of a given function. Input can be provided to the Fourier function using 3 different syntaxes.
- Fourier(x): In this method, x is the time domain function whereas the independent variable is determined by symvar and the transformation variable is w by default.
- Fourier(x,transvar): Here, x is the time domain function whereas transvar is the transformation variable instead of w.
- Fourier(x,indepvar,transvar): In this syntax, x is the time domain function whereas indepvar is the independent variable and transvar is the transformation variable instead of symvar and w respectively.
Now we find the Fourier Transform of  .
.
Example 1:
Matlab
syms t u
x = exp(-t^2-u^2);
X = fourier(x);
X1=fourier(x,y);
X2=fourier(x,t,y);
disp('1. Fourier Transform of exp(-t^2-u^2) using fourier(x) :')
disp(X);
disp('2. Fourier Transform of exp(-t^2-u^2) using fourier(x,y) :')
disp(X1);
disp('3. Fourier Transform of exp(-t^2-u^2) using fourier(x,t,y) :')
disp(X2);
|
Output:

Let’s take another example to find the Fourier Transform of a*abs(t).
Example 2:
Matlab
syms a t
x = a*abs(t);
X = fourier(x);
X1 = fourier(x,y);
X2 = fourier(x,t,y);
disp('1. Fourier Transform of a*abs(t) using fourier(x):')
disp(X);
disp('2. Fourier Transform of a*abs(t) using fourier(x,y):')
disp(X1);
disp('3. Fourier Transform of a*abs(t) using fourier(x,t,y):')
disp(X2);
|
Output:

Share your thoughts in the comments
Please Login to comment...