Forward and Inverse Fourier Transform of an Image in MATLAB
Last Updated :
28 Jan, 2022
In this article, we shall apply Fourier Transform on images. Fourier Transform is a mathematical technique that helps to transform Time Domain function x(t) to Frequency Domain function X(ω). In this article, we will see how to find Fourier Transform in MATLAB.
Properties of Fourier Transform:
- Linearity: The addition of two functions corresponding to the addition of the two frequency spectrum is called linearity. If we multiply a function by a constant, the Fourier transform of the resultant function is multiplied by the same constant. The Fourier transform of the sum of two or more functions is the sum of the Fourier transforms of the functions.
- Scaling: Scaling is the method that is used to change the range of the independent variables or features of data. If we stretch a function by the factor in the time domain then squeeze the Fourier transform by the same factor in the frequency domain.
- Differentiation: Differentiating function with respect to time yields to the constant multiple of the initial function.
- Convolution: It includes the multiplication of two functions. The Fourier transform of a convolution of two functions is the point-wise product of their respective Fourier transforms.
- Frequency Shift and Time Shift: Frequency is shifted according to the coordinates. There is a duality between the time and frequency domains and frequency shift affects the time shift. The time variable shift also affects the frequency function. The time-shifting property concludes that a linear displacement in time corresponds to a linear phase factor in the frequency domain.
The image chosen for the experiment in this article is a famous cameraman image.

Figure: Input image
Equation for DFT: ![Rendered by QuickLaTeX.com X(k) = \sum_{n=0}^{N-1}\ x[n].e^{\frac{-j2\pi kn}{N}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3516e8f716ef25550aeecfd01fe274b3_l3.png)
Equation for IDFT: ![Rendered by QuickLaTeX.com x(n) = \sum_{k=0}^{N-1}\ X[k].e^{\frac{j2\pi kn}{N}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-99fc81f7126067520eca19a30950d42d_l3.png)
Steps:
- Read the image.
- Apply forward Fourier transformation.
- Display log and shift FT images.
Function Used:
- imread( ) inbuilt function is used to image.
- fft2( ) inbuilt function is used to apply forward fourier transform on 2D signal.
- ifft2( ) inbuilt function is used to apply inverse Fourier transform on 2D signal.
- fftshift( ) inbuilt function is used to shift corners to center in FT image.
- log( ) inbuilt function is used to evaluate logarithm of FT complex signal.
- imtool( ) inbuilt function is used to display the image.
Example:
Matlab
k=imread("cameraman.jpg");
f=fft2(k);
f1=abs(f);
f2=log(abs(f));
f3=log(abs(fftshift(f)));
imtool(f1,[]);
imtool(f2,[]);
imtool(f3,[]);
f(1:20, 20:40)=0;
imtool(log(abs(f)),[]);
|
Output:
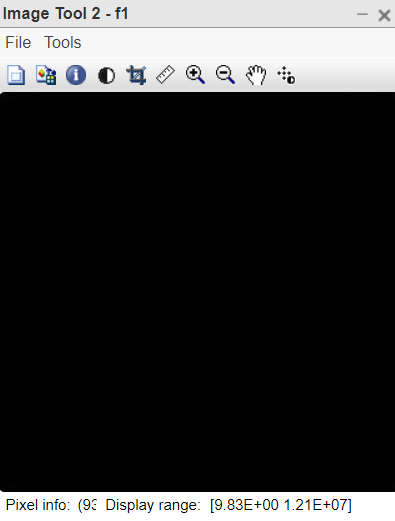
Figure 1:Absolute of the fourier transformed image
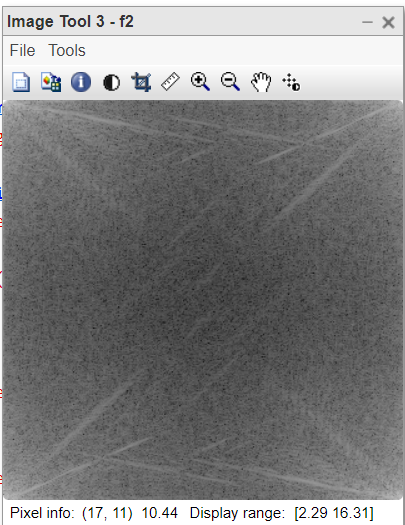
Figure 2: Log of the absolute of FT of image
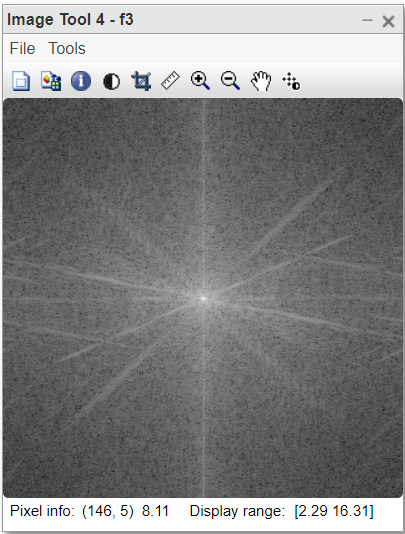
Figure 3:Centered spectrum of FT image
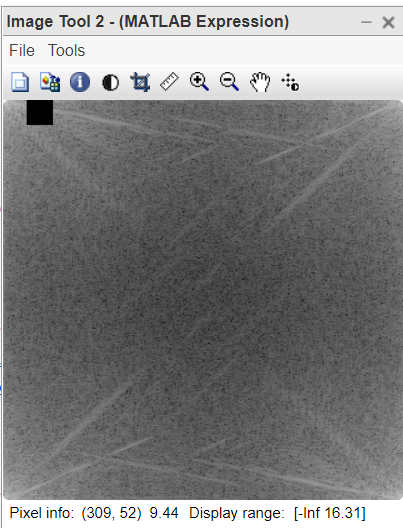
Figure 4: Some frequencies blocked in FT image
Code Explanation:
- k=imread(“cameraman.jpg”); This line reads the image.
- f=fft2(k); This line computes fourier transformation.
- f1=abs(f); This takes magnitude of FT.
- f2=log(abs(f)); This line takes log of magnitude of FT.
- f3=log(abs(fftshift(f))); This line shifts FT from corners to central part.
- f(1:20, 20:40)=0; This line remove frequencies from FT.
Example:
Matlab
j=ifft2(f);
j1=log(abs(j));
j2=fftshift(j);
j3=fftshift(j2);
f(1:20, 20:40)=0;
j4=ifft2(f);
imtool(j,[]);
imtool(j1,[]);
imtool(j2,[]);
imtool(j3,[]);
imtool(abs(j4),[]);
|
Output:

Figure 1:Original Input Image was obtained by taking the Inverse FT of the FT image
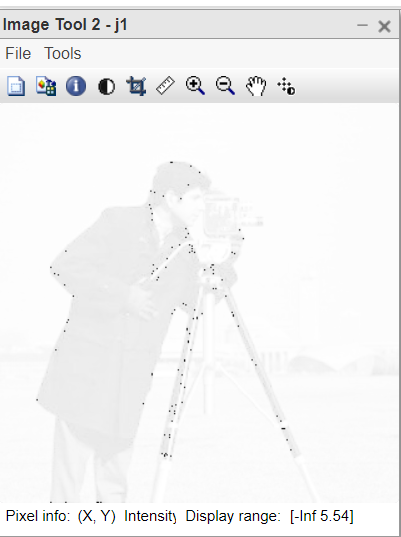
Figure 2: log of absolute Inverse Fourier Transformed Image

Figure 3: Corners shifted to center

Figure 4: Inverse FT after removing some frequencies from Freq Domain
Code Explanation:
- j=ifft2(f); This line computes inverse FT of FT image.
- f(1:20, 20:40)=0; This line removes some frequency from FT image.
- j4=ifft2(f); This line computes inverse FT after removing some frequencies.
- imtool(abs(j4),[]); This line displays modified image which contains some ringing artefacts.
Properties:
- There is no one-to-one correspondence between the cameraman image and the Fourier transform image.
- The cameraman image represents the intensities in the spatial domain.
- Fourier transformed image represents frequency in the frequency domain.
- Lower frequency represents the smooth part of the image while higher frequency represents the shape components like edges of an image.
- If the low-frequency part is removed from the frequency domain image then the spatial domain image will get blurred.
- If the anyone frequency value is removed (made 0) in the frequency domain image, that particular frequency will be removed (subtracted) from every intensity value in the spatial domain image.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...