Find the sum of n terms of the series 1 , 2a , 3a2 , 4a3 , 5a4 , …

Last Updated : 30 Aug, 2022

Given a series .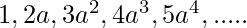 $1, 2a, 3a^{2}, 4a^{3}, 5a^{4},.....$ and the value of a. Find the sum of the first n term of the series.

Examples:

Input: a = 3, n = 4
Output: 142

Input: a = 5, n = 1
Output: 1

Brute Force Approach:

A simple approach can be iterating N terms of the series and adding them to calculate the sum for any value of a. Follow the steps below to understand the approach:

For each iteration:

Calculate aⁿ [ n = 0 ].
Multiply aⁿwith (n+1).
Add (n+1)*aⁿ to sum and increment n by 1.
Repeat the above processes n times.

Illustration:

a = 3 and n = 4

Loop will be executed n number of times i.e 4 in this case.

Loop 1: Initially the value of a = 1, n = 0, sum = 0

aⁿ= 3⁰
= 1
aⁿ* (n+1) = 3⁰* (0+1)
= 1 * (1)
= 1
sum = sum + aⁿ* (n+1)
= 0 + 1
= 1
Increment n by 1.

Loop 2: The value of a = 3, n = 1, sum = 1

aⁿ= 3¹
= 3
aⁿ* (n+1) = 3¹* (1+1)
= 3 * (2)
= 6
sum = sum + aⁿ* (n+1)
= 1 + 6
= 7
Increment value of n by 1.

Loop 3: The value of a = 3, n = 2, sum = 7

aⁿ= 3²
= 9
aⁿ* (n+1) = 3²* (2+1)
= 9 * (3)
= 27
sum = sum + aⁿ* (n+1)
= 7 + 27
= 34
Increment n by 1.

Loop 4: The value of a = 3, n = 3, sum = 34

aⁿ= 3³
= 27
aⁿ* (n+1) = 3³* (3+1)
= 27 * (4)
= 108
sum = sum + aⁿ* (n+1)
= 34 + 108
= 142
Increment the value of n by 1.

Below is the implementation of the above approach:

C++

// C++ implementation for the 
// approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to calculate 
// the sum
void calcSum(int a, int n)
{
  // Edge Cases
  if (n < 0) 
  {
    cout << "Invalid Input";
    return;
  }
 
  if (a == 0 || n == 1) 
  {
    cout << 1;
    return;
  }
 
  // Initialize the variables
  int Sum = 0;
 
  // Calculate Sum upto N terms
  for(int i = 0; i < n; i++)
  {
    int r = pow(a, (i)) * (i + 1);
    Sum += r;
  }
 
  // Print Sum
  cout << Sum;
}
 
// Driver Code
int main()
{
  int a = 3;
  int n = 4;
   
  // Invoke calcSum function with 
  // values of a and n
  calcSum(a, n);
  return 0;
}

Java

// Java implementation for the 
// approach
import java.util.*;
 
class GFG{
 
// Function to calculate 
// the sum
static void calcSum(int a, int n)
{
   
  // Edge Cases
  if (n < 0) 
  {
    System.out.print("Invalid Input");
    return;
  }
 
  if (a == 0 || n == 1) 
  {
    System.out.print(1);
    return;
  }
 
  // Initialize the variables
  int Sum = 0;
 
  // Calculate Sum upto N terms
  for(int i = 0; i < n; i++)
  {
    int r = (int) (Math.pow(a, (i)) * (i + 1));
    Sum += r;
  }
 
  // Print Sum
  System.out.print(Sum);
}
 
// Driver Code
public static void main(String[] args)
{
  int a = 3;
  int n = 4;
   
  // Invoke calcSum function with 
  // values of a and n
  calcSum(a, n);
}
}
 
// This code is contributed by 29AjayKumar

Python3

# Python 3 implementation for the
# approach
 
# Function to calculate
# the sum
def calcSum(a, n):
 
    # Edge Cases
    if (n < 0):
        print("Invalid Input")
        return
 
    if (a == 0 or n == 1):
 
        print(1)
        return
 
    # Initialize the variables
    Sum = 0
 
    # Calculate Sum upto N terms
    for i in range(n):
        r = pow(a, (i)) * (i + 1)
        Sum += r
 
    # Print Sum
    print(Sum)
 
# Driver Code
if __name__ == "__main__":
 
    a = 3
    n = 4
 
    # Invoke calcSum function with
    # values of a and n
    calcSum(a, n)
 
    # This code is contributed by ukasp.

C#

// C# program to find GCD of two
// numbers
using System;
using System.Collections;
 
class GFG {
 
// Function to calculate 
// the sum
static void calcSum(int a, int n)
{
  // Edge Cases
  if (n < 0) 
  {
    Console.Write("Invalid Input");
    return;
  }
 
  if (a == 0 || n == 1) 
  {
    Console.Write(1);
    return;
  }
 
  // Initialize the variables
  int Sum = 0;
 
  // Calculate Sum upto N terms
  for(int i = 0; i < n; i++)
  {
    int r = (int)Math.Pow(a, (i)) * (i + 1);
    Sum += r;
  }
 
  // Print Sum
  Console.Write(Sum);
}
 
// Driver method
public static void Main() 
{
    int a = 3;
    int n = 4;
   
    // Invoke calcSum function with 
    // values of a and n
    calcSum(a, n);
}
}
 
// This code is contributed by Samim Hossain Mondal.

Javascript

<script>
 
// JavaScript implementation for the  
// approach 
 
// Function to calculate 
// the sum
function calcSum(a, n) 
{
     
    // Edge Cases
    if (n < 0) 
    {
        document.write("Invalid Input");
        return;
    }
 
    if (a == 0 || n == 1)
    {
        document.write(1);
        return;
    }
 
    // Initialize the variables
    let Sum = 0;
 
    // Calculate Sum upto N terms
    for(let i = 0; i < n; i++) 
    {
        let r = Math.pow(a, (i)) * (i + 1);
        Sum += r;
    }
 
    // Print Sum
    document.write(Sum);
}
 
// Driver Code
let a = 3;
let n = 4;
 
// Invoke calcSum function with 
// values of a and n
calcSum(a, n);
 
// This code is contributed by Potta Lokesh
 
</script>

Output:

142

Time Complexity: O(nlogn) since it is using pow function inside a for loop
Auxiliary Space: O(1)

Efficient Approach

In this approach, an efficient solution is proposed using the concept of Geometric progression. The sum of the series of n terms in a Geometric Progression (G.P.) with first term a and common ratio r is given as:

$S_{n} = \frac{a(r^{n}-1)}{r - 1}$

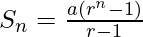
Let’s use this concept to reach a solution to the problem.

Let 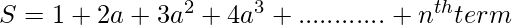$S = 1 +2a + 3a^{2} + 4a^{3} +............+n^{th} term$

Clearly nth term is 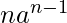$na^{n-1}$

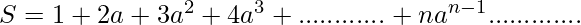$S = 1 +2a + 3a^{2} + 4a^{3} +............+na^{n-1}.............$ . (1)

Multiply both sides with ‘a’, we get,

$Sa = (1 +2a + 3a^{2} + 4a^{3} +............+na^{n-1})a$

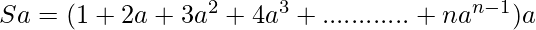
$Sa = 0 + a +2a^{2} + 3a^{3} + 4a^{4} +............+ (n - 1)a^{n - 1} + na^{n}............$ (2)

Subtracting equation (2) from (1), we get

$S - Sa = (1 +2a + 3a^{2} + 4a^{3} +............+na^{n-1}) - (0 + a +2a^{2} + 3a^{3} + 4a^{4} +............+ na^{n})$

$S(1 - a) = 1 + a + a^{2} + a^{3} +..............+ a^{n - 1} - na^{n}$

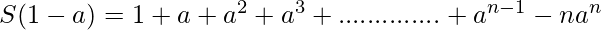
Clearly this is the Geometric Progression (G.P.) of n terms with first term 1 and common ration a.

G.P. of n terms with first term a and common ratio r is:

$S_{n} = \frac{a(r^{n}-1)}{r - 1}$

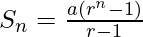
Using the above formula, we have

$S(1 - a) = \frac{1(a^{n} - 1)}{(a - 1)} - na^{n}$

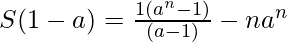
Dividing both sides by (1 – a), we get

$\frac{S(1 - a)}{(1 - a)} = \frac{1(a^{n} - 1)}{(a - 1)} * \frac{1}{(1 - a)} - na^{n} * \frac{1}{(1 - a)}$

$S = \frac{-1(1 - a^{n})}{(a - 1)} * \frac{-1}{(a - 1)} - \frac{na^{n}}{(1 - a)}$

$S = \frac{1(1 - a^{n})}{(a - 1)^{2}} - \frac{na^{n}}{(1 - a)}$

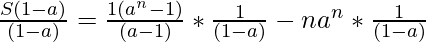
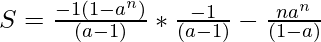
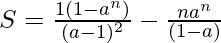
Therefore, the sum of the series 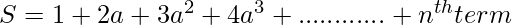$S = 1 +2a + 3a^{2} + 4a^{3} +............+n^{th} term$ is

$\frac{(1 - a^{n})}{(a - 1)^{2}} - \frac{na^{n}}{(1 - a)}$

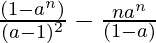
For a != 1 the formula for sum of the series is:

$S = \frac{(1 - a^{n})}{(a - 1)^{2}} - \frac{na^{n}}{(1 - a)}$

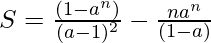
For a = 1 the formula for sum of the series is:
The series reduces to sum of first n natural numbers and the formula becomes-

$S = \frac{n(n + 1)}{2}$

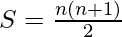
Illustration:

For a = 3, n = 4

Since a != 1, therefore use the formula

$S = \frac{(1 - a^{n})}{(a - 1)^{2}} - \frac{na^{n}}{(1 - a)}$

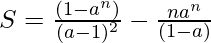
Substituting the values of a and n in the above formula, we get

$S = \frac{(1 - 3^{4})}{(3 - 1)^{2}} - \frac{4 * 3^{4}}{(1-3)}$

$S = \frac{1 - 81}{2^{2}} - \frac{324}{-2}$

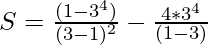
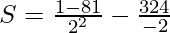
S = -20 – (-162)

S = 142

So, the sum of the series 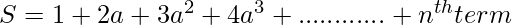$S = 1 +2a + 3a^{2} + 4a^{3} +............+n^{th} term$ with value of a = 3 and n = 4 is 142.

Below is the implementation of the above approach:

C++

// C++ program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to calculate 
// the sum
void calcSum(int a, int n)
{
  // Edge Cases
  if (n < 0) 
  {
    cout << "Invalid Input";
    return;
  }
 
  if (a == 0 || n == 1) 
  {
    cout << 1;
    return;
  }
 
  // Sum of First N Natural Numbers
  // In case a = 1
  if (a == 1) 
  {
    // Avoiding Overflow
    if (n % 2 == 0)
      cout << (n / 2) * (n + 1);
 
    else
      cout << ((n + 1) / 2) * n;
  }
 
  // Calculate Sum with the help 
  // of formula
  int r = pow(a, n);
  int d = pow(a - 1, 2);
  int Sum = (1 - r * (1 + n - n * a)) / d;
 
  // Print Sum
  cout << Sum;
}
 
// Driver Code
int main()
{
  int a = 3;
  int n = 4;
   
  // Invoke calcSum function 
  // with values of a and n
  calcSum(a, n);
  return 0;
}

Java

// Java program to implement
// the above approach
class GFG {
 
    // Function to calculate
    // the sum
    public static void calcSum(int a, int n)
    {
       
        // Edge Cases
        if (n < 0) {
            System.out.println("Invalid Input");
            return;
        }
 
        if (a == 0 || n == 1) {
            System.out.println(1);
            return;
        }
 
        // Sum of First N Natural Numbers
        // In case a = 1
        if (a == 1) {
            // Avoiding Overflow
            if (n % 2 == 0)
                System.out.println((n / 2) * (n + 1));
 
            else
                System.out.println(((n + 1) / 2) * n);
        }
 
        // Calculate Sum with the help
        // of formula
        int r = (int) Math.pow(a, n);
        int d = (int) Math.pow(a - 1, 2);
        int Sum = (1 - r * (1 + n - n * a)) / d;
 
        // Print Sum
        System.out.println(Sum);
    }
 
    // Driver Code
    public static void main(String args[]) {
        int a = 3;
        int n = 4;
 
        // Invoke calcSum function
        // with values of a and n
        calcSum(a, n);
    }
}
 
// This code is contributed by saurabh_jaiswal.

Python3

# Python program to implement
# the above approach
 
# Function to calculate
# the sum
def calcSum(a, n):
   
    # Edge Cases
    if (n < 0):
        print("Invalid Input");
        return;
 
    if (a == 0 or n == 1):
        print(1);
        return;
 
    # Sum of First N Natural Numbers
    # In case a = 1
    if (a == 1):
       
        # Avoiding Overflow
        if (n % 2 == 0):
            print((n // 2) * (n + 1));
 
        else:
            print(((n + 1) // 2) * n);
 
    # Calculate Sum with the help
    # of formula
    r =  pow(a, n);
    d = pow(a - 1, 2);
    Sum = (1 - r * (1 + n - n * a)) // d;
 
    # Print Sum
    print(Sum);
 
# Driver Code
if __name__ == '__main__':
    a = 3;
    n = 4;
 
    # Invoke calcSum function
    # with values of a and n
    calcSum(a, n);
 
# This code is contributed by 29AjayKumar 

C#

// C# program to implement
// the above approach
 
using System;
class GFG {
 
    // Function to calculate
    // the sum
    public static void calcSum(int a, int n)
    {
       
        // Edge Cases
        if (n < 0) {
            Console.WriteLine("Invalid Input");
            return;
        }
 
        if (a == 0 || n == 1) {
            Console.WriteLine(1);
            return;
        }
 
        // Sum of First N Natural Numbers
        // In case a = 1
        if (a == 1) {
            // Avoiding Overflow
            if (n % 2 == 0)
                Console.WriteLine((n / 2) * (n + 1));
 
            else
                Console.WriteLine(((n + 1) / 2) * n);
        }
 
        // Calculate Sum with the help
        // of formula
        int r = (int) Math.Pow(a, n);
        int d = (int) Math.Pow(a - 1, 2);
        int Sum = (1 - r * (1 + n - n * a)) / d;
 
        // Print Sum
        Console.WriteLine(Sum);
    }
 
    // Driver Code
    public static void Main() {
        int a = 3;
        int n = 4;
 
        // Invoke calcSum function
        // with values of a and n
        calcSum(a, n);
    }
}
 
// This code is contributed by gfgking.

Javascript

<script>
// Javascript program to implement
// the above approach
 
// Function to calculate 
// the sum
function calcSum(a, n)
{
  // Edge Cases
  if (n < 0) 
  {
    document.write("Invalid Input");
    return;
  }
 
  if (a == 0 || n == 1) 
  {
    document.write(1);
    return;
  }
 
  // Sum of First N Natural Numbers
  // In case a = 1
  if (a == 1) 
  {
    // Avoiding Overflow
    if (n % 2 == 0)
      document.write((n / 2) * (n + 1));
 
    else
      document.write(((n + 1) / 2) * n);
  }
 
  // Calculate Sum with the help 
  // of formula
  let r = Math.pow(a, n);
  let d = Math.pow(a - 1, 2);
  let Sum = (1 - r * (1 + n - n * a)) / d;
 
  // Print Sum
  document.write(Sum);
}
 
// Driver Code
let a = 3;
let n = 4;
   
// Invoke calcSum function 
// with values of a and n
calcSum(a, n);
 
// This code is contributed by Samim Hossain Mondal.
</script>

Output:

142

Time Complexity: O(logn) since it is using pow function pow(a,n)

Auxiliary Space: O(1)

Suggest improvement

Find the sum of N terms of the series 1, (2+3), (4+5+6), .....

Share your thoughts in the comments

Find the sum of n terms of the series 1 , 2a , 3a2 , 4a3 , 5a4 , …

C++

Java

Python3

C#

Javascript

C++

Java

Python3

C#

Javascript

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?