Find the sum of series 3, -6, 12, -24 . . . upto N terms
Last Updated :
23 Jun, 2022
Given an integer N. The task is to find the sum upto N terms of the given series:
3, -6, 12, -24, … upto N terms
Examples:
Input : N = 5
Output : Sum = 33
Input : N = 20
Output : Sum = -1048575
On observing the given series, it can be seen that the ratio of every term with their previous term is same which is -2. Hence the given series is a GP(Geometric Progression) series.
You can learn more about GP series here.
So, 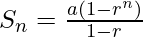 when r < 0.
when r < 0.
In above GP series the first term i:e a = 3 and common ratio i:e r = (-2).
Therefore, 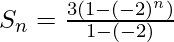 .
.
Thus, 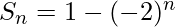 .
.
Below is the implementation of above approach:
C++
#include<iostream>
#include<math.h>
using namespace std;
class gfg
{
public:
int Sum_upto_nth_Term(int n)
{
return (1 - pow(-2, n));
}
};
int main()
{
gfg g;
int N = 5;
cout<<g.Sum_upto_nth_Term(N);
}
|
Java
import java.util.*;
class solution
{
static int Sum_upto_nth_Term(int n)
{
return (1 -(int)Math.pow(-2, n));
}
public static void main (String arr[])
{
int N = 5;
System.out.println(Sum_upto_nth_Term(N));
}
}
|
Python
def Sum_upto_nth_Term(n):
return (1 - pow(-2, n))
N = 5
print(Sum_upto_nth_Term(N))
|
C#
class GFG
{
static int Sum_upto_nth_Term(int n)
{
return (1 -(int)System.Math.Pow(-2, n));
}
public static void Main()
{
int N = 5;
System.Console.WriteLine(Sum_upto_nth_Term(N));
}
}
|
PHP
<?php
function Sum_upto_nth_Term($n)
{
return (1 - pow(-2, $n));
}
$N = 5;
echo (Sum_upto_nth_Term($N));
?>
|
Javascript
<script>
function Sum_upto_nth_Term( n) {
return (1 - parseInt( Math.pow(-2, n)));
}
let N = 5;
document.write(Sum_upto_nth_Term(N));
</script>
|
Time Complexity: O(logn), where n is the given integer.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Share your thoughts in the comments
Please Login to comment...