Find the player who will win the Coin game
Last Updated :
27 Sep, 2022
Given N coins, the task is to find who win the coin game.
Coin game is a game in which each player picks coins from the given N coins in such a way that he can pick coins ranging from 1 to 5 coins in one turn and the game continues for both the players. The player who picks the last coin loses the game.
Examples:
Input: N = 4
Output: First Player
Explanation:
Player 1 pick 3 coins and
Player 2 pick last coin
Input: N = 7
Output: Second Player
Approach:
- As the player can take coins ranging from 1 to 5 inclusively and if a player loses it means that he had only 1 coin, otherwise, he could have taken 1 less coin than available coins and force another player to lose. So now we will consider the case when the second player is going to win, which means the first player had only one coin.
- For N = 1, second player is going to win, for N = 2 to 6, first player can choose 1 less coin than N, and force the second player to lose so discard them, for N = 7, first player can choose coin 1 to 5, that’s going to leave coin ranging from 6 to 2, and then second player can choose 1 to 5, and to win second player will intelligently choose 1 less coin forcing first to lose, So basically starting from 1, all the numbers on a gap of 6(as whatever first player choose, second player will choose coins equal to difference of 6 and coins chosen by the first player) will be the winning for second player.
- Finally, we just have to check if n is of form 6*c+1 if it is then the second player going to win, otherwise, the first player going to win.
Below is the implementation for the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findWinner(int n)
{
if ((n - 1) % 6 == 0) {
cout << "Second Player wins the game";
}
else {
cout << "First Player wins the game";
}
}
int main()
{
int n = 7;
findWinner(n);
}
|
Java
class GFG
{
static void findWinner(int n)
{
if ((n - 1) % 6 == 0)
{
System.out.println("Second Player wins the game");
}
else
{
System.out.println("First Player wins the game");
}
}
public static void main(String[] args)
{
int n = 7;
findWinner(n);
}
}
|
Python3
def findWinner(n):
if ((n - 1) % 6 == 0):
print("Second Player wins the game");
else:
print("First Player wins the game");
if __name__ == '__main__':
n = 7;
findWinner(n);
|
C#
using System;
class GFG
{
static void findWinner(int n)
{
if ((n - 1) % 6 == 0)
{
Console.WriteLine("Second Player wins the game");
}
else
{
Console.WriteLine("First Player wins the game");
}
}
public static void Main()
{
int n = 7;
findWinner(n);
}
}
|
Javascript
<script>
function findWinner(n)
{
if ((n - 1) % 6 == 0) {
document.write("Second Player wins the game");
}
else {
document.write("First Player wins the game");
}
}
var n = 7;
findWinner(n);
</script>
|
Output:
Second Player wins the game
Time Complexity: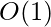
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...