Let us solve the classic “fake coin” puzzle using decision trees. There are the two different variants of the puzzle given below. I am providing description of both the puzzles below, try to solve on your own, assume N = 8.
Easy: Given a two pan fair balance and N identically looking coins, out of which only one coin is lighter (or heavier). To figure out the odd coin, how many minimum number of weighing are required in the worst case?
Difficult: Given a two pan fair balance and N identically looking coins out of which only one coin may be defective. How can we trace which coin, if any, is odd one and also determine whether it is lighter or heavier in minimum number of trials in the worst case?
Let us start with relatively simple examples. After reading every problem try to solve on your own.
Problem 1: (Easy)
Given 5 coins out of which one coin is lighter. In the worst case, how many minimum number of weighing are required to figure out the odd coin?
Name the coins as 1, 2, 3, 4 and 5. We know that one coin is lighter. Considering best out come of balance, we can group the coins in two different ways, [(1, 2), (3, 4) and (5)], or [(12), (34) and (5)]. We can easily rule out groups like [(123) and (45)], as we will get obvious answer. Any other combination will fall into one of these two groups, like [(2)(45) and (13)], etc.
Consider the first group, pairs (1, 2) and (3, 4). We can check (1, 2), if they are equal we go ahead with (3, 4). We need two weighing in worst case. The same analogy can be applied when the coin in heavier.
With the second group, weigh (12) and (34). If they balance (5) is defective one, otherwise pick the lighter pair, and we need one more weighing to find odd one.
Both the combinations need two weighing in case of 5 coins with prior information of one coin is lighter.
Analysis: In general, if we know that the coin is heavy or light, we can trace the coin in log3(N) trials (rounded to next integer). If we represent the outcome of balance as ternary tree, every leaf represent an outcome. Since any coin among N coins can be defective, we need to get a 3-ary tree having minimum of N leaves. A 3-ary tree at k-th level will have 3k leaves and hence we need 3k >= N.
In other-words, in k trials we can examine upto 3k coins, if we know whether the defective coin is heavier or lighter. Given that a coin is heavier, verify that 3 trials are sufficient to find the odd coin among 12 coins, because 32 < 12 < 33.
Problem 2: (Difficult)
We are given 4 coins, out of which only one coin may be defective. We don’t know, whether all coins are genuine or any defective one is present. How many number of weighing are required in worst case to figure out the odd coin, if present? We also need to tell whether it is heavier or lighter.
From the above analysis we may think that k = 2 trials are sufficient, since a two level 3-ary tree yields 9 leaves which is greater than N = 4 (read the problem once again). Note that it is impossible to solve above 4 coins problem in two weighing. The decision tree confirms the fact (try to draw).
We can group the coins in two different ways, [(12, 34)] or [(1, 2) and (3, 4)]. Let us consider the combination (12, 34), the corresponding decision tree is given below. Blue leaves are valid outcomes, and red leaves are impossible cases. We arrived at impossible cases due to the assumptions made earlier on the path.

The outcome can be (12) < (34) i.e. we go on to left subtree or (12) > (34) i.e. we go on to right subtree.
The left subtree is possible in two ways,
- A) Either 1 or 2 can be lighter OR
- B) Either 3 or 4 can be heavier.
Further on the left subtree, as second trial, we weigh (1, 2) or (3, 4). Let us consider (3, 4) as the analogy for (1, 2) is similar. The outcome of second trail can be three ways
- A) (3) < (4) yielding 4 as defective heavier coin, OR
- B) (3) > (4) yielding 3 as defective heavier coin OR
- C) (3) = (4), yielding ambiguity. Here we need one more weighing to check a genuine coin against 1 or 2. In the figure I took (3, 2) where 3 is confirmed as genuine. We can get (3) > (2) in which 2 is lighter, or (3) = (2) in which 1 is lighter. Note that it impossible to get (3) < (2), it contradicts our assumption leaned to left side.
Similarly we can analyze the right subtree. We need two more weighings on right subtree as well.
Overall we need 3 weighings to trace the odd coin. Note that we are unable to utilize two outcomes of 3-ary trees. Also, the tree is not full tree, middle branch terminated after first weighing. Infact, we can get 27 leaves of 3 level full 3-ary tree, but only we got 11 leaves including impossible cases.
Analysis: Given N coins, all may be genuine or only one coin is defective. We need a decision tree with atleast (2N + 1) leaves correspond to the outputs. Because there can be N leaves to be lighter, or N leaves to be heavier or one genuine case, on total (2N + 1) leaves.
As explained earlier ternary tree at level k, can have utmost 3k leaves and we need a tree with leaves of 3k > (2N + 1).
In other words, we need atleast k > log3(2N + 1) weighing to find the defective one.
Observe the above figure that not all the branches are generating leaves, i.e. we are missing valid outputs under some branches that leading to more number of trials. When possible, we should group the coins in such a way that every branch is going to yield valid output (in simple terms generate full 3-ary tree). Problem 4 describes this approach of 12 coins.
Problem 3: (Special case of two pan balance)
We are given 5 coins, a group of 4 coins out of which one coin is defective (we don’t know whether it is heavier or lighter), and one coin is genuine. How many weighing are required in worst case to figure out the odd coin whether it is heavier or lighter?
Label the coins as 1, 2, 3, 4 and G (genuine). We now have some information on coin purity. We need to make use that in the groupings.
We can best group them as [(G1, 23) and (4)]. Any other group can’t generate full 3-ary tree, try yourself. The following diagram explains the procedure.
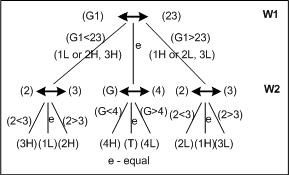
The middle case (G1) = (23) is self explanatory, i.e. 1, 2, 3 are genuine and 4th coin can be figured out lighter or heavier in one more trial.
The left side of tree corresponds to the case (G1) < (23). This is possible in two ways, either 1 should be lighter or either of (2, 3) should be heavier. The former instance is obvious when next weighing (2, 3) is balanced, yielding 1 as lighter. The later instance could be (2) < (3) yielding 3 as heavier or (2) > (3) yielding 2 as heavier. The leaf nodes on left branch are named to reflect these outcomes.
The right side of tree corresponds to the case (G1) > (23). This is possible in two ways, either 1 is heavier or either of (2, 3) should be lighter. The former instance is obvious when the next weighing (2, 3) is balanced, yielding 1 as heavier. The later case could be (2) < (3) yielding 2 as lighter coin, or (2) > (3) yielding 3 as lighter.
In the above problem, under any possibility we need only two weighing. We are able to use all outcomes of two level full 3-ary tree. We started with (N + 1) = 5 coins where N = 4, we end up with (2N + 1) = 9 leaves. Infact we should have 11 outcomes since we started with 5 coins, where are other 2 outcomes? These two outcomes can be declared at the root of tree itself (prior to first weighing), can you figure these two out comes?
If we observe the figure, after the first weighing the problem reduced to “we know three coins, either one can be lighter (heavier) or one among other two can be heavier (lighter)”. This can be solved in one weighing (read Problem 1).
Analysis: Given (N + 1) coins, one is genuine and the rest N can be genuine or only one coin is defective. The required decision tree should result in minimum of (2N + 1) leaves. Since the total possible outcomes are (2(N + 1) + 1), number of weighing (trials) are given by the height of ternary tree, k >= log3[2(N + 1) + 1]. Note the equality sign.
Rearranging k and N, we can weigh maximum of N <= (3k – 3)/2 coins in k trials.
Problem 4: (The classic 12 coin puzzle)
You are given two pan fair balance. You have 12 identically looking coins out of which one coin may be lighter or heavier. How can you find odd coin, if any, in minimum trials, also determine whether defective coin is lighter or heavier, in the worst case?
How do you want to group them? Bi-set or tri-set? Clearly we can discard the option of dividing into two equal groups. It can’t lead to best tree. From the above two examples, we can ensure that the decision tree can be used in optimal way if we can reveal atleast one genuine coin. Remember to group coins such that the first weighing reveals atleast one genuine coin.
Let us name the coins as 1, 2, … 8, A, B, C and D. We can combine the coins into 3 groups, namely (1234), (5678) and (ABCD). Weigh (1234) and (5678). You are encouraged to draw decision tree while reading the procedure. The outcome can be three ways,
- (1234) = (5678), both groups are equal. Defective coin may be in (ABCD) group.
- (1234) < (5678), i.e. first group is less in weight than second group.
- (1234) > (5678), i.e. first group is more in weight than second group.
The output (1) can be solved in two more weighing as special case of two pan balance given in Problem 3. We know that groups (1234) and (5678) are genuine and defective coin may be in (ABCD). Pick one genuine coin from any of weighed groups, and proceed with (ABCD) as explained in Problem 3.
Outcomes (2) and (3) are special. In both the cases, we know that (ABCD) is genuine. And also, we know a set of coins being lighter and a set of coins being heavier. We need to shuffle the weighed two groups in such a way that we end up with smaller height decision tree.
Consider the second outcome where (1234) < (5678). It is possible when any coin among (1, 2, 3, 4) is lighter or any coin among (5, 6, 7, 8 ) is heavier. We revealed lighter or heavier possibility after first weighing. If we proceed as in Problem 1, we will not generate best decision tree. Let us shuffle coins as (1235) and (4BCD) as new groups (there are different shuffles possible, they also lead to minimum weighing). If we weigh these two groups again the outcome can be three ways, i) (1235) < (4BCD) yielding one among 1, 2, 3 is lighter which is similar to Problem 1 explained above, we need one more weighing, ii) (1235) = (4BCD) yielding one among 6, 7, 8 is heavier which is similar to Problem 1 explained above, we need one more weighing iii) (1235) > (4BCD) yielding either 5 as heavier coin or 4 as lighter coin, at the expense of one more weighing.
Similar way we can also solve the right subtree (third outcome where (1234) > (5678)) in two more weighing.
We are able to solve the 12 coin puzzle in 3 weighing in the worst case.
Few Interesting Puzzles:
- Solve Problem 4 with N = 8 and N = 13, How many minimum trials are required in each case?
- Given a function int weigh(A[], B[]) where A and B are arrays (need not be equal size). The function returns -1, 0 or 1. It returns 0 if sum of all elements in A and B are equal, -1 if A < B and 1 if A > B. Given an array of 12 elements, all elements are equal except one. The odd element can be as that of others, smaller or greater than others. Write a program to find the odd element (if any) using weigh() minimum number of times.
- You might have seen 3-pan balance in science labs during school days. Given a 3-pan balance (4 outcomes) and N coins, how many minimum trials are needed to figure out odd coin?
References:
Similar problem was provided in one of the exercises of the book “Introduction to Algorithms by Levitin”. Specifically read section 5.5 and section 11.2 including exercises.
– – – by Venki.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...