Minimum Players required to win the game
Last Updated :
25 Jul, 2022
Given N questions and K options for each question, where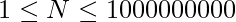 
and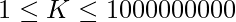 
. The task is to determine the sum of total number of player who has attempted ith question for all 
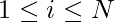to win the game anyhow. You have to minimize the sum of a total number of player and output it modulo 109+7.
Note: Any wrong answer leads to elimination of the player.
Examples:
Input: N = 3, K = 3
Output: 39
Input: N = 5, K = 2
Output: 62
Approach:
- To solve Nth question K players are needed.
- To solve (N-1)th question K2 players are needed.
- Similarly moving onwards, To solve 1st question KN players are needed.
So, our problem reduces to finding the sum of GP terms K + K2 + … + KN which is equal to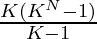 
.
Now we can use Fermat’s Little Theorem to get the required answer modulo with 109+7.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define mod 1000000007
long long int power(long long int a, long long int b)
{
long long int res = 1;
while (b) {
if (b & 1) {
res *= a;
res %= mod;
}
b /= 2;
a *= a;
a %= mod;
}
return res;
}
long long int minPlayer(long long int n, long long int k)
{
long long int num = ((power(k, n) - 1) + mod) % mod;
long long int den = (power(k - 1, mod - 2) + mod) % mod;
long long int ans = (((num * den) % mod) * k) % mod;
return ans;
}
int main()
{
long long int n = 3, k = 3;
cout << minPlayer(n, k);
return 0;
}
|
Java
public class TYU {
static long mod = 1000000007;
static long power(long a, long b)
{
long res = 1;
while (b != 0) {
if ((b & 1) != 0) {
res *= a;
res %= mod;
}
b /= 2;
a *= a;
a %= mod;
}
return res;
}
static long minPlayer(long n, long k)
{
long num = ((power(k, n) - 1) + mod) % mod;
long den = (power(k - 1, mod - 2) + mod) % mod;
long ans = (((num * den) % mod) * k) % mod;
return ans;
}
public static void main(String[] args) {
long n = 3, k = 3;
System.out.println(minPlayer(n, k));
}
}
|
Python 3
mod = 1000000007
def power(a, b) :
res = 1
while(b) :
if (b & 1) :
res *= a
res %= mod
b //= 2
a *= a
a %= mod
return res
def minPlayer(n, k) :
num = ((power(k, n) - 1) + mod) % mod
den = (power(k - 1,mod - 2) + mod) % mod
ans = (((num * den) % mod ) * k) % mod
return ans
if __name__ == "__main__" :
n, k = 3, 3
print(minPlayer(n, k))
|
C#
using System;
class GFG
{
static long mod = 1000000007;
static long power(long a, long b)
{
long res = 1;
while (b != 0)
{
if ((b & 1) != 0)
{
res *= a;
res %= mod;
}
b /= 2;
a *= a;
a %= mod;
}
return res;
}
static long minPlayer(long n, long k)
{
long num = ((power(k, n) - 1) + mod) % mod;
long den = (power(k - 1, mod - 2) + mod) % mod;
long ans = (((num * den) % mod) * k) % mod;
return ans;
}
public static void Main()
{
long n = 3, k = 3;
Console.WriteLine(minPlayer(n, k));
}
}
|
PHP
<?php
function power($a, $b)
{
$mod = 1000000007;
$res = 1;
while ($b)
{
if ($b & 1)
{
$res *= $a;
$res %= $mod;
}
$b /= 2;
$a *= $a;
$a %= $mod;
}
return $res;
}
function minPlayer($n, $k)
{
$mod =1000000007;
$num = ((power($k, $n) - 1) +
$mod) % $mod;
$den = (power($k - 1, $mod - 2) +
$mod) % $mod;
$ans = ((($num * $den) % $mod) *
$k) % $mod;
return $ans;
}
$n = 3;
$k = 3;
echo minPlayer($n, $k);
?>
|
Javascript
<script>
var mod = 107;
function power(a , b) {
var res = 1;
while (b != 0) {
if ((b & 1) != 0) {
res *= a;
res = res%mod;
}
b = parseInt(b/2);
a *= a;
a %= mod;
}
return res;
}
function minPlayer(n , k) {
var num = ((power(k, n) - 1) + mod) % mod;
var den = (power(k - 1, mod - 2) + mod) % mod;
var ans = (((num * den) % mod) * k) % mod;
return ans;
}
var n = 3, k = 3;
document.write(minPlayer(n, k));
</script>
|
Time Complexity: O(log(n)), Auxiliary Space: O (1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...