Find the length of Kth N-sided polygon formed by given operations
Last Updated :
20 Jul, 2022
Given an integer L, representing the side length of an N-sided regular polygon and integer K, the task is to find the side length of the Kth N-sided regular polygon formed inside the (K – 1)th regular polygon by connecting midpoints of the sides of the (K – 1)th polygon.
Examples:
Input: N = 3, L = 6, K = 2
Output: 3
Input: N = 5, L = 21, K = 7
Output: 5.88796
Approach: The given problem can be solved based on the following observations:

- Suppose, \theta represents the interior angle of the N-sided polygon which is the same for all the polygons formed inside i.e.,
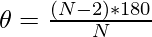
- The length of the side of the first polygon formed inside by connecting midpoints of the sides can be calculated using the formula as
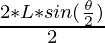 .
. - The length of the side of the Kth polygon formed inside the (K – 1)th polygon and connecting midpoints of the sides of the (K – 1)th polygon is
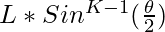
Follow the steps below to solve the problem:
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define PI 3.14159265
double findInteriorAngle(int n)
{
return (n - 2) * PI / n;
}
double calculateSideLength(double L,
int N, int K)
{
double angle = findInteriorAngle(N);
double length = L * pow(sin(angle / 2),
(K - 1));
return length;
}
int main()
{
double N = 5, L = 21, K = 7;
cout << calculateSideLength(L, N, K);
return 0;
}
|
Java
import java.util.*;
class GFG{
static final double PI = 3.14159265;
static double findInteriorAngle(int n)
{
return ((n - 2) * PI) / n;
}
static double calculateSideLength(double L,
int N, int K)
{
double angle = findInteriorAngle(N);
double length = L * Math.pow(Math.sin(angle / 2),
(K - 1));
return length;
}
public static void main(String[] args)
{
double L = 21;
int N = 5, K = 7;
System.out.print(calculateSideLength(L, N, K));
}
}
|
Python3
import math
PI = 3.14159265
def findInteriorAngle(n):
return (n - 2) * PI / n
def calculateSideLength(L,
N, K):
angle = findInteriorAngle(N)
length = L * pow(math.sin(angle / 2),
(K - 1))
return length
if __name__ == "__main__":
N = 5
L = 21
K = 7
print(calculateSideLength(L, N, K))
|
C#
using System;
class GFG{
static readonly double PI = 3.14159265;
static double findInteriorAngle(int n)
{
return ((n - 2) * PI) / n;
}
static double calculateSideLength(double L,
int N, int K)
{
double angle = findInteriorAngle(N);
double length = L * Math.Pow(Math.Sin(angle / 2),
(K - 1));
return length;
}
public static void Main(String[] args)
{
double L = 21;
int N = 5, K = 7;
Console.Write(calculateSideLength(L, N, K));
}
}
|
Javascript
<script>
const PI = 3.14159265
function findInteriorAngle(n)
{
return (n - 2) * PI / n;
}
function calculateSideLength(L,
N, K) {
let angle = findInteriorAngle(N);
let length = L * Math.pow(Math.sin(angle / 2),
(K - 1));
return length;
}
let N = 5
let L = 21
let K = 7;
document.write(calculateSideLength(L, N, K))
</script>
|
Time Complexity: O(log K)
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...