Apothem of a n-sided regular polygon

Given here the side length a of a regular n-sided polygon, the task is to find the length of its Apothem. 
Apothem is the line drawn from the center of the polygon that is perpendicular to one of its sides. 
Examples:

Input a = 9, n = 6
Output: 7.79424

Input: a = 8, n = 7
Output: 8.30609

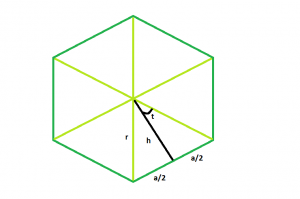
Approach: 

In the figure, we see the polygon can be divided into n equal triangles. 
Looking into one of the triangles, we see the whole angle at the centre can be divided into = 360/n
So, angle t = 180/n
now, tan t = a/2h
So, h = a/(2*tan t)
here, h is the apothem, 
so, apothem = a/(2*tan(180/n))

Below is the implementation of the above approach.

C++

// C++ Program to find the apothem
// of a regular polygon with given side length
#include <bits/stdc++.h>
using namespace std;

// Function to find the apothem
// of a regular polygon
float polyapothem(float n, float a)
{

    // Side and side length cannot be negative
    if (a < 0 && n < 0)
        return -1;

    // Degree converted to radians
    return a / (2 * tan((180 / n) * 3.14159 / 180));
}

// Driver code
int main()
{
    float a = 9, n = 6;
    cout << polyapothem(n, a) << endl;

    return 0;
}

Java

// Java Program to find the apothem of a
// regular polygon with given side length
import java.util.*;

class GFG
{

    // Function to find the apothem
    // of a regular polygon
    double polyapothem(double n, double a)
    {

        // Side and side length cannot be negative
        if (a < 0 && n < 0)
            return -1;

        // Degree converted to radians
        return (a / (2 * java.lang.Math.tan((180 / n)
                * 3.14159 / 180)));
    }

// Driver code
public static void main(String args[])
{
    double a = 9, n = 6;
    GFG g=new GFG();
    System.out.println(g.polyapothem(n, a));
}

}
//This code is contributed by Shivi_Aggarwal

Python3

# Python 3 Program to find the apothem
# of a regular polygon with given side
# length
from math import tan

# Function to find the apothem
# of a regular polygon
def polyapothem(n, a):

    # Side and side length cannot be negative
    if (a < 0 and n < 0):
        return -1

    # Degree converted to radians
    return a / (2 * tan((180 / n) *
                   3.14159 / 180))

# Driver code
if __name__ == '__main__':
    a = 9
    n = 6
    print('{0:.6}'.format(polyapothem(n, a)))

# This code is contributed by
# Sahil_Shelangia

C#

// C# Program to find the apothem of a
// regular polygon with given side length
using System;

class GFG
{

// Function to find the apothem
// of a regular polygon
static double polyapothem(double n,
                          double a)
{

    // Side and side length cannot
    // be negative
    if (a < 0 && n < 0)
        return -1;

    // Degree converted to radians
    return (a / (2 * Math.Tan((180 / n) *
                       3.14159 / 180)));
}

// Driver code
public static void Main()
{
    double a = 9, n = 6;
    Console.WriteLine(Math.Round(polyapothem(n, a), 4));
}
}

// This code is contributed by Ryuga

PHP

<?php
// PHP Program to find the apothem of a
// regular polygon with given side length

// Function to find the apothem
// of a regular polygon
function polyapothem($n, $a)
{

    // Side and side length cannot
    // be negative
    if ($a < 0 && $n < 0)
        return -1;

    // Degree converted to radians
    return $a / (2 * tan((180 / $n) *
                    3.14159 / 180));
}

// Driver code
$a = 9; $n = 6;
echo polyapothem($n, $a) . "\n";

// This code is contributed
// by Akanksha Rai
?>

Javascript

<script>
// javascript Program to find the apothem of a
// regular polygon with given side length

// Function to find the apothem
// of a regular polygon
function polyapothem(n , a)
{

    // Side and side length cannot be negative
    if (a < 0 && n < 0)
        return -1;

    // Degree converted to radians
    return (a / (2 * Math.tan((180 / n)
            * 3.14159 / 180)));
}

// Driver code

var a = 9, n = 6;

document.write(polyapothem(n, a).toFixed(5));


// This code contributed by Princi Singh
</script>

Output:

7.79424

Time Complexity: O(1)

Auxiliary Space: O(1)