Find the integral roots of a given Cubic equation
Last Updated :
01 Nov, 2023
Given 5 integers say A, B, C, D, and E which represents the cubic equation 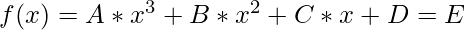 , the task is to find the integral solution for this equation. If there doesn’t exist any integral solution then print “NA”.
, the task is to find the integral solution for this equation. If there doesn’t exist any integral solution then print “NA”.
Examples:
Input: A = 1, B = 0, C = 0, D = 0, E = 27
Output: 3
Input: A = 1, B = 0, C = 0, D = 0, E = 16
Output: NA
Approach: The idea is to use binary search. Below are the steps:
- Initialise the start and end variable as 0 & 105 respectively.
- Find the middle(say mid) value of start and end check if it satisfy the given equation or not.
- If current mid satisfy the given equation then print the mid value.
- Else if the value of f(x) is less than E then update start as mid + 1.
- Else Update end as mid – 1.
- If we can’t find any integral solution for the above equation then print “-1”.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
long long int check(int A, int B, int C,
int D, long long int x)
{
long long int ans;
ans = (A * x * x * x
+ B * x * x
+ C * x
+ D);
return ans;
}
void findSolution(int A, int B, int C,
int D, int E)
{
int start = 0, end = 100000;
long long int mid, ans;
while (start <= end) {
mid = start + (end - start) / 2;
ans = check(A, B, C, D, mid);
if (ans == E) {
cout << mid << endl;
return;
}
if (ans < E)
start = mid + 1;
else
end = mid - 1;
}
cout << "NA";
}
int main()
{
int A = 1, B = 0, C = 0;
int D = 0, E = 27;
findSolution(A, B, C, D, E);
}
|
Java
import java.util.*;
class GFG{
static long check(int A, int B, int C,
int D, long x)
{
long ans;
ans = (A * x * x * x +
B * x * x + C * x + D);
return ans;
}
static void findSolution(int A, int B, int C,
int D, int E)
{
long start = 0, end = 100000;
long mid, ans;
while (start <= end)
{
mid = start + (end - start) / 2;
ans = check(A, B, C, D, mid);
if (ans == E)
{
System.out.println(mid);
return;
}
if (ans < E)
start = mid + 1;
else
end = mid - 1;
}
System.out.println("NA");
}
public static void main(String args[])
{
int A = 1, B = 0, C = 0;
int D = 0, E = 27;
findSolution(A, B, C, D, E);
}
}
|
Python3
def check(A, B, C, D, x) :
ans = 0;
ans = (A * x * x * x +
B * x * x + C * x + D);
return ans;
def findSolution(A, B, C, D, E) :
start = 0; end = 100000;
mid = 0;
ans = 0;
while (start <= end) :
mid = start + (end - start) // 2;
ans = check(A, B, C, D, mid);
if (ans == E) :
print(mid);
return;
if (ans < E) :
start = mid + 1;
else :
end = mid - 1;
print("NA");
if __name__ == "__main__" :
A = 1; B = 0; C = 0;
D = 0; E = 27;
findSolution(A, B, C, D, E);
|
C#
using System;
class GFG{
static long check(int A, int B, int C,
int D, long x)
{
long ans;
ans = (A * x * x * x +
B * x * x + C * x + D);
return ans;
}
static void findSolution(int A, int B, int C,
int D, int E)
{
long start = 0, end = 100000;
long mid, ans;
while (start <= end)
{
mid = start + (end - start) / 2;
ans = check(A, B, C, D, mid);
if (ans == E)
{
Console.WriteLine(mid);
return;
}
if (ans < E)
start = mid + 1;
else
end = mid - 1;
}
Console.Write("NA");
}
public static void Main()
{
int A = 1, B = 0, C = 0;
int D = 0, E = 27;
findSolution(A, B, C, D, E);
}
}
|
Javascript
<script>
function check(A, B, C, D, x)
{
var ans;
ans = (A * x * x * x +
B * x * x + C * x + D);
return ans;
}
function findSolution(A, B, C, D, E)
{
var start = 0, end = 100000;
var mid, ans;
while (start <= end)
{
mid = parseInt(start + (end - start) / 2);
ans = check(A, B, C, D, mid);
if (ans == E)
{
document.write(mid);
return;
}
if (ans < E)
start = mid + 1;
else
end = mid - 1;
}
document.write("NA");
}
var A = 1, B = 0, C = 0;
var D = 0, E = 27;
findSolution(A, B, C, D, E);
</script>
|
Time Complexity: O(log N)
Auxiliary Space: O(1) as constant space for variables is being used
Share your thoughts in the comments
Please Login to comment...