Find sum of even index binomial coefficients

Given a positive integer n. The task is to find the sum of even indexed binomial coefficient. That is,
ⁿC₀ + ⁿC₂ + ⁿC₄ + ⁿC₆ + ⁿC₈ + ………..
Examples :

Input : n = 4
Output : 8
Explanation:
⁴C₀ + ⁴C₂ + ⁴C₄
= 1 + 6 + 1
= 8
Input : n = 6
Output : 32

Method 1: (Brute Force)
The idea is to find all the binomial coefficients and find only the sum of even indexed values.

CPP

// CPP Program to find sum
// of even index term
#include <bits/stdc++.h>
using namespace std;
 
// Return the sum of
// even index term
int evenSum(int n)
{
    int C[n + 1][n + 1];
    int i, j;
 
    // Calculate value of Binomial
    // Coefficient in bottom up manner
    for (i = 0; i <= n; i++) {
        for (j = 0; j <= min(i, n); j++) {
            // Base Cases
            if (j == 0 || j == i)
                C[i][j] = 1;
 
            // Calculate value using
            // previously stored values
            else
                C[i][j] = C[i - 1][j - 1]
                            + C[i - 1][j];
        }
    }   
 
    // finding sum of even index term.
    int sum = 0;
    for (int i = 0; i <= n; i += 2)
        sum += C[n][i];
 
    return sum;
}
 
// Driver Program
int main()
{
    int n = 4;
    cout << evenSum(n) << endl;
    return 0;
}

Java

// Java Program to find sum
// of even index term
import java.io.*;
import java.math.*;
 
class GFG {
     
    // Return the sum of
    // even index term
    static int evenSum(int n)
    {
        int C[][] = new int [n + 1][n + 1];
        int i, j;
      
        // Calculate value of Binomial
        // Coefficient in bottom up manner
        for (i = 0; i <= n; i++)
        {
            for (j = 0; j <= Math.min(i, n); j++)
            {
                // Base Cases
                if (j == 0 || j == i)
                    C[i][j] = 1;
      
                // else Calculate value using
                // previously stored values
                else
                    C[i][j] = C[i - 1][j - 1]
                                + C[i - 1][j];
            }
        }   
      
        // finding sum of even index term.
        int sum = 0;
        for (i = 0; i <= n; i += 2)
            sum += C[n][i];
      
        return sum;
    }
      
    // Driver Program
    public static void main(String args[])
    {
        int n = 4;
        System.out.println(evenSum(n));
    }
}
 
/*This code is contributed by Nikita Tiwari.*/

Python

# Python Program to find sum of even index term
import math
 
# Return the sum of even index term
def evenSum(n) :
    # Creates a list containing n+1 lists,
    # each of n+1 items, all set to 0
    C = [[0 for x in range(n + 1)] for y in range(n + 1)]
 
    # Calculate value of Binomial Coefficient
    # in bottom up manner
    for i in range(0, n + 1):
        for j in range(0, min(i, n + 1)):
            # Base Cases
            if j == 0 or j == i:
                C[i][j] = 1
 
            # Calculate value using previously
            # stored values
            else:
                C[i][j] = C[i - 1][j - 1] + C[i - 1][j]
         
    # Finding sum of even index term
    sum = 0;
    for i in range(0, n + 1):
        if n % 2 == 0:
            sum = sum + C[n][i]
             
    return sum
     
# Driver method
n = 4
print evenSum(n)
 
 
# This code is contributed by 'Gitanjali'.

C#

// C# Program to find sum
// of even index term
using System;
 
class GFG {
     
    // Return the sum of
    // even index term
    static int evenSum(int n)
    {
        int [,]C = new int [n + 1,n + 1];
        int i, j;
     
        // Calculate value of Binomial
        // Coefficient in bottom up manner
        for (i = 0; i <= n; i++)
        {
            for (j = 0; j <= Math.Min(i, n); j++)
            {
                // Base Cases
                if (j == 0 || j == i)
                    C[i,j] = 1;
     
                // else Calculate value using
                // previously stored values
                else
                    C[i,j] = C[i - 1,j - 1]
                            + C[i - 1,j];
            }
        }
     
        // finding sum of even index term.
        int sum = 0;
        for (i = 0; i <= n; i += 2)
            sum += C[n,i];
     
        return sum;
    }
     
    // Driver Program
    public static void Main()
    {
        int n = 4;
        Console.WriteLine(evenSum(n));
    }
}
 
/*This code is contributed by vt_m.*/

PHP

<?php
// PHP Program to find sum
// of even index term
 
// Return the sum of
// even index term
function evenSum($n)
{
    $C = array(array());
    $i; $j;
 
    // Calculate value of Binomial
    // Coefficient in bottom up manner
    for ($i = 0; $i <= $n; $i++)
    {
        for ($j = 0; $j <= min($i, $n); $j++)
        {
            // Base Cases
            if ($j == 0 or $j == $i)
                $C[$i][$j] = 1;
 
            // Calculate value using
            // previously stored values
            else
                $C[$i][$j] = $C[$i - 1][$j - 1] +
                             $C[$i - 1][$j];
        }
    }
 
    // finding sum of even index term.
    $sum = 0;
    for ( $i = 0; $i <= $n; $i += 2)
        $sum += $C[$n][$i];
 
    return $sum;
}
 
// Driver Code
$n = 4;
echo evenSum($n) ;
 
// This code is contributed by anuj_67.
?>

Javascript

<script>
 
// Javascript Program to find sum
// of even index term
 
// Return the sum of
// even index term
function evenSum(n)
{
    var C =  Array.from(Array(n+1),
    ()=> Array(n+1).fill(0));
    var i, j;
 
    // Calculate value of Binomial
    // Coefficient in bottom up manner
    for (i = 0; i <= n; i++) {
        for (j = 0; j <= Math.min(i, n); j++) {
            // Base Cases
            if (j == 0 || j == i)
                C[i][j] = 1;
 
            // Calculate value using
            // previously stored values
            else
                C[i][j] = C[i - 1][j - 1]
                            + C[i - 1][j];
        }
    }   
 
    // finding sum of even index term.
    var sum = 0;
    for (var i = 0; i <= n; i += 2)
        sum += C[n][i];
 
    return sum;
}
 
// Driver Program
var n = 4;
document.write( evenSum(n) );  
 
</script>   

Output

Time Complexity: O(n²)
Auxiliary Space: O(n²)

Method 2: (Using Formula)
Sum of even indexed binomial coefficient :
$^nC_0 + ^nC_2 + ^nC_4 + ^nC_6 + .... = 2^{n-1}$
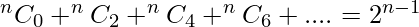
Proof :

We know,
(1 + x)ⁿ = ⁿC₀ + ⁿC₁ x + ⁿC₂ x² + ..... + ⁿC_n xⁿ

Now put x = -x, we get
(1 - x)ⁿ = ⁿC₀ - ⁿC₁ x + ⁿC₂ x² + ..... + (-1)ⁿ ⁿC_n xⁿ

Now, adding both the above equation, we get,
(1 + x)ⁿ + (1 - x)ⁿ = 2 * [ⁿC₀ + ⁿC₂ x² + ⁿC₄ x⁴ + .......]

Put x = 1
(1 + 1)ⁿ + (1 - 1)ⁿ = 2 * [ⁿC₀ + ⁿC₂ + ⁿC₄ + .......]
2ⁿ/2 = ⁿC₀ + ⁿC₂ + ⁿC₄ + .......
2^n-1 = ⁿC₀ + ⁿC₂ + ⁿC₄ + .......

Below is the implementation of this approach :

C++

// CPP Program to find sum even indexed Binomial
// Coefficient.
#include <bits/stdc++.h>
using namespace std;
 
// Returns value of even indexed Binomial Coefficient
// Sum which is 2 raised to power n-1.
int evenbinomialCoeffSum(int n)
{
    return (1 << (n - 1));
}
 
/* Driver program to test above function*/
int main()
{
    int n = 4;
    printf("%d", evenbinomialCoeffSum(n));
    return 0;
}

Java

// Java Program to find sum even indexed
// Binomial Coefficient.
import java.io.*;
 
class GFG {
// Returns value of even indexed Binomial Coefficient
// Sum which is 2 raised to power n-1.
static int evenbinomialCoeffSum(int n)
{
    return (1 << (n - 1));
}
 
// Driver Code
public static void main(String[] args)
{
int n = 4;
    System.out.println(evenbinomialCoeffSum(n));
}
    }
 
// This code is contributed by 'Gitanjali'.

Python

# Python program to find sum even indexed
# Binomial Coefficient
import math
 
# Returns value of even indexed Binomial Coefficient
# Sum which is 2 raised to power n-1.
def evenbinomialCoeffSum( n):
 
    return (1 << (n - 1))
 
# Driver method
if __name__ == '__main__':
    n = 4
    print evenbinomialCoeffSum(n)
 
# This code is contributed by 'Gitanjali'.

C#

// C# Program to find sum even indexed
// Binomial Coefficient.
using System;
 
class GFG
{
    // Returns value of even indexed
    // Binomial Coefficient Sum which
    // is 2 raised to power n-1.
    static int evenbinomialCoeffSum(int n)
    {
        return (1 << (n - 1));
    }
     
    // Driver Code
    public static void Main()
    {
        int n = 4;
        Console.WriteLine(evenbinomialCoeffSum(n));
    }
}
 
// This code is contributed by 'Vt_m'.

PHP

<?php
// PHP Program to find sum
// even indexed Binomial
// Coefficient.
 
// Returns value of even indexed
// Binomial Coefficient Sum which
// is 2 raised to power n-1.
function evenbinomialCoeffSum( $n)
{
    return (1 << ($n - 1));
}
 
    // Driver Code
    $n = 4;
    echo evenbinomialCoeffSum($n);
 
// This code is contributed by anuj_67.
?>

Javascript

<script>
 
// JavaScript Program to find sum even indexed
// Binomial Coefficient.
 
// Returns value of even indexed Binomial Coefficient
// Sum which is 2 raised to power n-1.
function evenbinomialCoeffSum(n)
{
    return (1 << (n - 1));
}
 
// Driver code   
                  
        let n = 4;
    document.write(evenbinomialCoeffSum(n));
      
     // This code is contributed by code_hunt.
</script>