Sum of all products of the Binomial Coefficients of two numbers up to K
Last Updated :
10 May, 2021
Given three integers N, M and K, the task is to calculate the sum of products of Binomial Coefficients C(N, i) and C(M, K – i), where i ranges between [0, K].
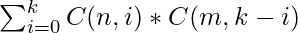
Examples:
Input: N = 2, M = 2, K = 2
Output: 6
Explanation:
C(2, 0) * C(2, 2) + C(2, 1) * C(2, 1) + C(2, 2) * C(2, 0) = 1*1 + 2*2 +1*1 = 6
Input: N = 2, M = 3, K = 1
Output: 5
Explanation:
C(2, 0) * C(3, 1) + C(2, 1) * C(3, 0) = 1*3 + 2*1 = 5
Naive Approach:The simplest approach to solve this problem is to simply iterate over the range [0, K] and calculate C(N, i) and C(M, K – 1) for every i and update sum by adding their product.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int nCr(int n, int r)
{
int res = 1;
if (r > n - r)
r = n - r;
for (int i = 0; i < r; ++i) {
res *= (n - i);
res /= (i + 1);
}
return res;
}
int solve(int n, int m, int k)
{
int sum = 0;
for (int i = 0; i <= k; i++)
sum += nCr(n, i)
* nCr(m, k - i);
return sum;
}
int main()
{
int n = 3, m = 2, k = 2;
cout << solve(n, m, k);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int nCr(int n, int r)
{
int res = 1;
if (r > n - r)
r = n - r;
for (int i = 0; i < r; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
static int solve(int n, int m, int k)
{
int sum = 0;
for (int i = 0; i <= k; i++)
sum += nCr(n, i)
* nCr(m, k - i);
return sum;
}
public static void main(String[] args)
{
int n = 3, m = 2, k = 2;
System.out.print(solve(n, m, k));
}
}
|
Python3
def nCr(n, r):
res = 1
if r > n - r:
r = n - r
for i in range(r):
res *= (n - i)
res /= (i + 1)
return res;
def solve(n, m, k):
sum = 0;
for i in range(k + 1):
sum += nCr(n, i) * nCr(m, k - i)
return int(sum)
if __name__ == '__main__':
n = 3
m = 2
k = 2;
print(solve(n, m, k))
|
C#
using System;
class GFG{
static int nCr(int n, int r)
{
int res = 1;
if (r > n - r)
r = n - r;
for (int i = 0; i < r; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
static int solve(int n, int m, int k)
{
int sum = 0;
for (int i = 0; i <= k; i++)
sum += nCr(n, i)
* nCr(m, k - i);
return sum;
}
public static void Main(String[] args)
{
int n = 3, m = 2, k = 2;
Console.Write(solve(n, m, k));
}
}
|
Javascript
<script>
function nCr(n, r)
{
let res = 1;
if (r > n - r)
r = n - r;
for (let i = 0; i < r; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
function solve(n, m, k)
{
let sum = 0;
for (let i = 0; i <= k; i++)
sum += nCr(n, i)
* nCr(m, k - i);
return sum;
}
let n = 3, m = 2, k = 2;
document.write(solve(n, m, k));
</script>
|
Time complexity: O(K2)
Auxiliary Space: O(1)
Efficient Approach:
The above approach can be optimized using Vandermonde’s Identity.
According to Vandermonde’s Identity, any combination of K items from a total of (N + M) items should have r items from M and (K – r) items from N items.
Therefore, the given expression is reduced to the following:
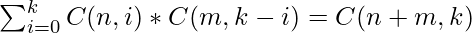
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int nCr(int n, int r)
{
int res = 1;
if (r > n - r)
r = n - r;
for (int i = 0; i < r; ++i) {
res *= (n - i);
res /= (i + 1);
}
return res;
}
int main()
{
int n = 3, m = 2, k = 2;
cout << nCr(n + m, k);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int nCr(int n, int r)
{
int res = 1;
if (r > n - r)
r = n - r;
for (int i = 0; i < r; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
public static void main(String[] args)
{
int n = 3, m = 2, k = 2;
System.out.print(nCr(n + m, k));
}
}
|
Python3
def nCr(n, r):
res = 1
if(r > n - r):
r = n - r
for i in range(r):
res *= (n - i)
res //= (i + 1)
return res
if __name__ == '__main__':
n = 3
m = 2
k = 2
print(nCr(n + m, k))
|
C#
using System;
class GFG{
static int nCr(int n, int r)
{
int res = 1;
if (r > n - r)
r = n - r;
for (int i = 0; i < r; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
public static void Main()
{
int n = 3, m = 2, k = 2;
Console.Write(nCr(n + m, k));
}
}
|
Javascript
<script>
function nCr(n, r)
{
let res = 1;
if (r > n - r)
r = n - r;
for (let i = 0; i < r; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
let n = 3, m = 2, k = 2;
document.write(nCr(n + m, k));
</script>
|
Time Complexity: O(K)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...