Calculate area of a cyclic quadrilateral with given side lengths
Last Updated :
04 Oct, 2021
Given four positive integers A, B, C, and D representing the length of sides of a Cyclic Quadrilateral, the task is to find the area of the Cyclic Quadrilateral.
Examples:
Input: A = 10, B = 15, C = 20, D = 25
Output: 273.861
Input: A = 10, B = 30, C = 50, D = 20
Output: 443.706
Approach: The given problem can be solved based on the following observations:
- A cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. The circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic.

- In the above image above r is the radius of the circumcircle and A, B, C, and D are the lengths of the sides PQ, QR, RS, and SP respectively.
- The area of the quadrilateral is given by Bretschneider’s formula is:
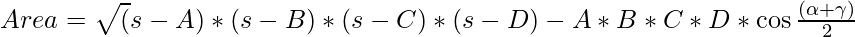
where, A, B, C, and D are the sides of the triangle and
? and ? are the opposite angles of the quadrilateral.
Since, the sum of opposite angles of the quadrilateral is 180 degree. Therefore, the value of cos(180/2) = cos(90) = 0.
Therefore, the formula for finding the area reduces to 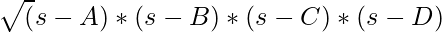 .
.
Therefore, the idea is to print the value of 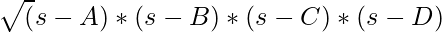 as the resultant area of the given quadrilateral.
as the resultant area of the given quadrilateral.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float calculateArea(float A, float B,
float C, float D)
{
float S = (A + B + C + D) / 2;
float area = sqrt((S - A) * (S - B)
* (S - C) * (S - D));
return area;
}
int main()
{
float A = 10;
float B = 15;
float C = 20;
float D = 25;
cout << calculateArea(A, B, C, D);
return 0;
}
|
Java
import java.io.*;
class GFG{
static float calculateArea(float A, float B,
float C, float D)
{
float S = (A + B + C + D) / 2;
float area = (float)Math.sqrt((S - A) * (S - B) *
(S - C) * (S - D));
return area;
}
public static void main (String[] args)
{
float A = 10;
float B = 15;
float C = 20;
float D = 25;
System.out.println(calculateArea(A, B, C, D));
}
}
|
Python3
from math import sqrt
def calculateArea(A, B, C, D):
S = (A + B + C + D) // 2
area = sqrt((S - A) * (S - B) *
(S - C) * (S - D))
return area
if __name__ == '__main__':
A = 10
B = 15
C = 20
D = 25
print(round(calculateArea(A, B, C, D), 3))
|
C#
using System;
class GFG{
static float calculateArea(float A, float B,
float C, float D)
{
float S = (A + B + C + D) / 2;
float area = (float)Math.Sqrt((S - A) * (S - B) *
(S - C) * (S - D));
return area;
}
static public void Main()
{
float A = 10;
float B = 15;
float C = 20;
float D = 25;
Console.Write(calculateArea(A, B, C, D));
}
}
|
Javascript
<script>
function calculateArea(A, B, C, D){
let S = (A + B + C + D) /2
let area = Math.sqrt((S - A) * (S - B) *
(S - C) * (S - D))
return area;
}
let A = 10;
let B = 15;
let C = 20;
let D = 25;
document.write(calculateArea(A, B, C, D).toFixed(3))
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...