Find if there is a path of more than k length from a source

Given a graph, a source vertex in the graph and a number k, find if there is a simple path (without any cycle) starting from given source and ending at any other vertex such that the distance from source to that vertex is atleast ‘k’ length.

Example:

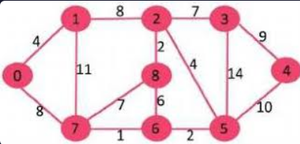
Weighted Undirected Graph

Input  : Source s = 0, k = 58
Output : True
There exists a simple path 0 -> 7 -> 1
-> 2 -> 8 -> 6 -> 5 -> 3 -> 4
Which has a total distance of 60 km which
is more than 58.

Input  : Source s = 0, k = 62
Output : False

In the above graph, the longest simple
path has distance 61 (0 -> 7 -> 1-> 2
 -> 3 -> 4 -> 5-> 6 -> 8, so output 
should be false for any input greater 
than 61.

We strongly recommend you to minimize your browser and try this yourself first.

One important thing to note is, simply doing BFS or DFS and picking the longest edge at every step would not work. The reason is, a shorter edge can produce longer path due to higher weight edges connected through it.

The idea is to use Backtracking. We start from given source, explore all paths from current vertex. We keep track of current distance from source. If distance becomes more than k, we return true. If a path doesn’t produces more than k distance, we backtrack.

How do we make sure that the path is simple and we don’t loop in a cycle? The idea is to keep track of current path vertices in an array. Whenever we add a vertex to path, we check if it already exists or not in current path. If it exists, we ignore the edge.

Below is implementation of above idea. 

C++

// Program to find if there is a simple path with
// weight more than k
#include<bits/stdc++.h>
using namespace std;

// iPair ==>  Integer Pair
typedef pair<int, int> iPair;

// This class represents a dipathted graph using
// adjacency list representation
class Graph
{
    int V;    // No. of vertices

    // In a weighted graph, we need to store vertex
    // and weight pair for every edge
    list< pair<int, int> > *adj;
    bool pathMoreThanKUtil(int src, int k, vector<bool> &path);

public:
    Graph(int V);  // Constructor

    // function to add an edge to graph
    void addEdge(int u, int v, int w);
    bool pathMoreThanK(int src, int k);
};

// Returns true if graph has path more than k length
bool Graph::pathMoreThanK(int src, int k)
{
    // Create a path array with nothing included
    // in path
    vector<bool> path(V, false);

    // Add source vertex to path
    path[src] = 1;

    return pathMoreThanKUtil(src, k, path);
}

// Prints shortest paths from src to all other vertices
bool Graph::pathMoreThanKUtil(int src, int k, vector<bool> &path)
{
    // If k is 0 or negative, return true;
    if (k <= 0)
        return true;

    // Get all adjacent vertices of source vertex src and
    // recursively explore all paths from src.
    list<iPair>::iterator i;
    for (i = adj[src].begin(); i != adj[src].end(); ++i)
    {
        // Get adjacent vertex and weight of edge
        int v = (*i).first;
        int w = (*i).second;

        // If vertex v is already there in path, then
        // there is a cycle (we ignore this edge)
        if (path[v] == true)
            continue;

        // If weight of is more than k, return true
        if (w >= k)
            return true;

        // Else add this vertex to path
        path[v] = true;

        // If this adjacent can provide a path longer
        // than k, return true.
        if (pathMoreThanKUtil(v, k-w, path))
            return true;

        // Backtrack
        path[v] = false;
    }

    // If no adjacent could produce longer path, return
    // false
    return false;
}

// Allocates memory for adjacency list
Graph::Graph(int V)
{
    this->V = V;
    adj = new list<iPair> [V];
}

// Utility function to an edge (u, v) of weight w
void Graph::addEdge(int u, int v, int w)
{
    adj[u].push_back(make_pair(v, w));
    adj[v].push_back(make_pair(u, w));
}

// Driver program to test methods of graph class
int main()
{
    // create the graph given in above figure
    int V = 9;
    Graph g(V);

    //  making above shown graph
    g.addEdge(0, 1, 4);
    g.addEdge(0, 7, 8);
    g.addEdge(1, 2, 8);
    g.addEdge(1, 7, 11);
    g.addEdge(2, 3, 7);
    g.addEdge(2, 8, 2);
    g.addEdge(2, 5, 4);
    g.addEdge(3, 4, 9);
    g.addEdge(3, 5, 14);
    g.addEdge(4, 5, 10);
    g.addEdge(5, 6, 2);
    g.addEdge(6, 7, 1);
    g.addEdge(6, 8, 6);
    g.addEdge(7, 8, 7);

    int src = 0;
    int k = 62;
    g.pathMoreThanK(src, k)? cout << "Yes\n" :
                             cout << "No\n";

    k = 60;
    g.pathMoreThanK(src, k)? cout << "Yes\n" :
                             cout << "No\n";

    return 0;
}

Java

// Java Program to find if there is a simple path with
// weight more than k
import java.util.*;
public class GFG{

  static class AdjListNode {
    int v;
    int weight;

    AdjListNode(int _v, int _w)
    {
      v = _v;
      weight = _w;
    }
    int getV() { return v; }
    int getWeight() { return weight; }
  }

  // This class represents a dipathted graph using
  // adjacency list representation
  static class Graph
  {
    int V; // No. of vertices

    // In a weighted graph, we need to store vertex
    // and weight pair for every edge
    ArrayList<ArrayList<AdjListNode>> adj;

    // Allocates memory for adjacency list
    Graph(int V)
    {
      this.V = V;
      adj = new ArrayList<ArrayList<AdjListNode>>(V);

      for(int i = 0; i < V; i++)
      {
        adj.add(new ArrayList<AdjListNode>());
      }
    }

    // Utility function to an edge (u, v) of weight w
    void addEdge(int u, int v, int weight)
    {
      AdjListNode node1 = new AdjListNode(v, weight);
      adj.get(u).add(node1); // Add v to u's list

      AdjListNode node2 = new AdjListNode(u, weight);
      adj.get(v).add(node2); // Add u to v's list
    }

    // Returns true if graph has path more than k length
    boolean pathMoreThanK(int src, int k)
    {

      // Create a path array with nothing included
      // in path
      boolean path[] = new boolean[V];

      Arrays.fill(path, false);

      // Add source vertex to path
      path[src] = true;

      return pathMoreThanKUtil(src, k, path);
    }

    // Prints shortest paths from src to all other vertices
    boolean pathMoreThanKUtil(int src, int k, boolean[] path)
    {

      // If k is 0 or negative, return true;
      if (k <= 0)
        return true;

      // Get all adjacent vertices of source vertex src and
      // recursively explore all paths from src.
      ArrayList<AdjListNode> it = adj.get(src);

      int index = 0;
      for(int i = 0; i < adj.get(src).size(); i++)
      {
        AdjListNode vertex = adj.get(src).get(i);

        // Get adjacent vertex and weight of edge
        int v = vertex.v;
        int w = vertex.weight;

        // increase theindex
        index++;

        // If vertex v is already there in path, then
        // there is a cycle (we ignore this edge)
        if (path[v] == true)
          continue;

        // If weight of is more than k, return true
        if (w >= k)
          return true;

        // Else add this vertex to path
        path[v] = true;

        // If this adjacent can provide a path longer
        // than k, return true.
        if (pathMoreThanKUtil(v, k-w, path))
          return true;

        // Backtrack
        path[v] = false;
      }

      // If no adjacent could produce longer path, return
      // false
      return false;
    }

  }

  // Driver program to test methods of graph class
  public static void main(String[] args)
  {

    // create the graph given in above figure
    int V = 9;
    Graph g = new Graph(V);

    // making above shown graph
    g.addEdge(0, 1, 4);
    g.addEdge(0, 7, 8);
    g.addEdge(1, 2, 8);
    g.addEdge(1, 7, 11);
    g.addEdge(2, 3, 7);
    g.addEdge(2, 8, 2);
    g.addEdge(2, 5, 4);
    g.addEdge(3, 4, 9);
    g.addEdge(3, 5, 14);
    g.addEdge(4, 5, 10);
    g.addEdge(5, 6, 2);
    g.addEdge(6, 7, 1);
    g.addEdge(6, 8, 6);
    g.addEdge(7, 8, 7);

    int src = 0;
    int k = 62;

    if(g.pathMoreThanK(src, k))
      System.out.println("YES");
    else
      System.out.println("NO");


    k = 60;
    if(g.pathMoreThanK(src, k))
      System.out.println("YES");
    else
      System.out.println("NO");

  }
}

// This code is contributed by adityapande88.

Python3

# Program to find if there is a simple path with
# weight more than k

# This class represents a dipathted graph using
# adjacency list representation
class Graph:
    # Allocates memory for adjacency list
    def __init__(self, V):
        self.V = V
        self.adj = [[] for i in range(V)]

    # Returns true if graph has path more than k length
    def pathMoreThanK(self,src, k):
        # Create a path array with nothing included
        # in path
        path = [False]*self.V

        # Add source vertex to path
        path[src] = 1

        return self.pathMoreThanKUtil(src, k, path)

    # Prints shortest paths from src to all other vertices
    def pathMoreThanKUtil(self,src, k, path):
        # If k is 0 or negative, return true
        if (k <= 0):
            return True

        # Get all adjacent vertices of source vertex src and
        # recursively explore all paths from src.
        i = 0
        while i != len(self.adj[src]):
            # Get adjacent vertex and weight of edge
            v = self.adj[src][i][0]
            w = self.adj[src][i][1]
            i += 1

            # If vertex v is already there in path, then
            # there is a cycle (we ignore this edge)
            if (path[v] == True):
                continue

            # If weight of is more than k, return true
            if (w >= k):
                return True

            # Else add this vertex to path
            path[v] = True

            # If this adjacent can provide a path longer
            # than k, return true.
            if (self.pathMoreThanKUtil(v, k-w, path)):
                return True

            # Backtrack
            path[v] = False

        # If no adjacent could produce longer path, return
        # false
        return False

    # Utility function to an edge (u, v) of weight w
    def addEdge(self,u, v, w):
        self.adj[u].append([v, w])
        self.adj[v].append([u, w])

# Driver program to test methods of graph class
if __name__ == '__main__':

    # create the graph given in above figure
    V = 9
    g = Graph(V)

    #  making above shown graph
    g.addEdge(0, 1, 4)
    g.addEdge(0, 7, 8)
    g.addEdge(1, 2, 8)
    g.addEdge(1, 7, 11)
    g.addEdge(2, 3, 7)
    g.addEdge(2, 8, 2)
    g.addEdge(2, 5, 4)
    g.addEdge(3, 4, 9)
    g.addEdge(3, 5, 14)
    g.addEdge(4, 5, 10)
    g.addEdge(5, 6, 2)
    g.addEdge(6, 7, 1)
    g.addEdge(6, 8, 6)
    g.addEdge(7, 8, 7)

    src = 0
    k = 62
    if g.pathMoreThanK(src, k):
        print("Yes")
    else:
        print("No")

    k = 60
    if g.pathMoreThanK(src, k):
        print("Yes")
    else:
        print("No")

C#

// C# Program to find if there is a simple path with
// weight more than k
using System;
using System.Collections.Generic;

class Program
{

  // Driver program to test methods of graph class
  static void Main(string[] args)
  {

    // create the graph given in above figure
    int V = 9;
    Graph g = new Graph(V);

    // making above shown graph
    g.addEdge(0, 1, 4);
    g.addEdge(0, 7, 8);
    g.addEdge(1, 2, 8);
    g.addEdge(1, 7, 11);
    g.addEdge(2, 3, 7);
    g.addEdge(2, 8, 2);
    g.addEdge(2, 5, 4);
    g.addEdge(3, 4, 9);
    g.addEdge(3, 5, 14);
    g.addEdge(4, 5, 10);
    g.addEdge(5, 6, 2);
    g.addEdge(6, 7, 1);
    g.addEdge(6, 8, 6);
    g.addEdge(7, 8, 7);

    int src = 0;
    int k = 62;

    if (g.pathMoreThanK(src, k))
      Console.WriteLine("YES");
    else
      Console.WriteLine("NO");

    k = 60;
    if (g.pathMoreThanK(src, k))
      Console.WriteLine("YES");
    else
      Console.WriteLine("NO");
  }
}

class AdjListNode {
  public int v;
  public int weight;

  public AdjListNode(int _v, int _w)
  {
    v = _v;
    weight = _w;
  }
  public int getV() { return v; }
  public int getWeight() { return weight; }
}

// This class represents a dipathted graph using
// adjacency list representation
class Graph {
  public int V; // No. of vertices

  // In a weighted graph, we need to store vertex
  // and weight pair for every edge
  public List<List<AdjListNode> > adj
    = new List<List<AdjListNode> >();

  // Allocates memory for adjacency list
  public Graph(int V)
  {
    this.V = V;
    for (int i = 0; i < V; i++)
      adj.Add(new List<AdjListNode>());
  }

  // Utility function to an edge (u, v) of weight w
  public void addEdge(int u, int v, int weight)
  {
    AdjListNode node1 = new AdjListNode(v, weight);
    adj[u].Add(node1); // Add v to u's list

    AdjListNode node2 = new AdjListNode(u, weight);
    adj[v].Add(node2); // Add u to v's list
  }

  // Prints shortest paths from src to all other vertices
  bool pathMoreThanKUtil(int src, int k, bool[] path)
  {
    // If k is 0 or negative, return true;
    if (k <= 0)
      return true;

    // Get all adjacent vertices of source vertex src
    // and recursively explore all paths from src.
    List<AdjListNode> it = adj[src];

    for (int i = 0; i < adj[src].Count; i++) {
      AdjListNode vertex = adj[src][i];

      // Get adjacent vertex and weight of edge
      int v = vertex.v;
      int w = vertex.weight;

      // If vertex v is already there in path, then
      // there is a cycle (we ignore this edge)
      if (path[v] == true)
        continue;

      // If weight of is more than k, return true
      if (w >= k)
        return true;

      // Else add this vertex to path
      path[v] = true;

      // If this adjacent can provide a path longer
      // than k, return true.
      if (pathMoreThanKUtil(v, k - w, path))
        return true;

      // Backtrack
      path[v] = false;
    }

    // If no adjacent could produce longer path, return
    // false
    return false;
  }

  // Returns true if graph has path more than k length
  public bool pathMoreThanK(int src, int k)
  {
    // Create a path array with nothing included
    // in path
    bool[] path = new bool[V];

    for (int i = 0; i < V; i++)
      path[i] = false;

    // Add source vertex to path
    path[src] = true;
    return pathMoreThanKUtil(src, k, path);
  }
}

// This code is contributed by Tapesh (tapeshdua420)

Javascript

// JavaScript Program to find if there is a simple path with
// weight more than k
class AdjListNode {
    constructor(v, weight) {
        this.v = v;
        this.weight = weight;
    }
}

// This class represents a dipathted graph using
// adjacency list representation
class Graph {
    // Allocates memory for adjacency list
    constructor(V) {
        this.V = V; // No. of vertices

        // In a weighted graph, we need to store vertex
        // and weight pair for every edge
        this.adj = [];
        for (var i = 0; i < V; i++) {
            this.adj[i] = [];
        }
    }

    // Utility function to an edge (u, v) of weight w
    addEdge(u, v, weight) {
        var node1 = new AdjListNode(v, weight);
        this.adj[u].push(node1); // Add v to u's list
        var node2 = new AdjListNode(u, weight);
        this.adj[v].push(node2); // Add u to v's list
    }

    // Prints shortest paths from src to all other vertices
    pathMoreThanKUtil(src, k, path) {

        // If k is 0 or negative, return true;
        if (k <= 0)
            return true;

        // Get all adjacent vertices of source vertex src and
        // recursively explore all paths from src.
        var it = this.adj[src];

        for (var i = 0; i < this.adj[src].length; i++) {
            var vertex = this.adj[src][i];

            // Get adjacent vertex and weight of edge
            var v = vertex.v;
            var w = vertex.weight;

            // If vertex v is already there in path, then
            // there is a cycle (we ignore this edge)
            if (path[v] == true)
                continue;

            // If weight of is more than k, return true
            if (w >= k)
                return true;

            // Else add this vertex to path
            path[v] = true;

            // If this adjacent can provide a path longer
            // than k, return true.
            if (this.pathMoreThanKUtil(v, k - w, path))
                return true;

            // Backtrack
            path[v] = false;
        }
        // If no adjacent could produce longer path, return
        // false
        return false;
    }

    // Returns true if graph has path more than k length
    pathMoreThanK(src, k) {
        // Create a path array with nothing included
        // in path
        var path = new Array(V);
        for (var i = 0; i < V; i++) {
            path[i] = false;
        }
        // Add source vertex to path
        path[src] = true;
        return this.pathMoreThanKUtil(src, k, path);
    }
}

// Driver program to test methods of graph class

// create the graph given in above figure
var V = 9;
var g = new Graph(V);

// making above shown graph
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);

var src = 0;
var k = 62;

if (g.pathMoreThanK(src, k)) {
    console.log("YES");
} else {
    console.log("NO");
}

k = 60

if (g.pathMoreThanK(src, k)) {
    console.log("YES");
} else {
    console.log("NO");
}

// This code is contributed by Tapesh(tapeshdua420)

Output:

No
Yes

Exercise: 
Modify the above solution to find weight of longest path from a given source.

Time Complexity: The time complexity of this algorithm is O(V+E) where V is the number of vertices and E is the number of edges in the graph. This is because the algorithm performs a depth-first search through the graph, visiting each vertex and checking if there is a path with a weight greater than k.

Auxiliary Space: O(V)

Explanation:

From the source node, we one-by-one visit all the paths and check if the total weight is greater than k for each path. So, the worst case will be when the number of possible paths is maximum. This is the case when every node is connected to every other node. 

Beginning from the source node we have n-1 adjacent nodes. The time needed for a path to connect any two nodes is 2. One for joining the source and the next adjacent vertex. One for breaking the connection between the source and the old adjacent vertex. 

After selecting a node out of n-1 adjacent nodes, we are left with n-2 adjacent nodes (as the source node is already included in the path) and so on at every step of selecting a node our problem reduces by 1 node.

We can write this in the form of a recurrence relation as: F(n) = n*(2+F(n-1))  This expands to: 2n + 2n*(n-1) + 2n*(n-1)*(n-2) + ……. + 2n(n-1)(n-2)(n-3)…..1  As n times 2n(n-1)(n-2)(n-3)….1 is greater than the given expression so we can safely say time complexity is: n*2*n!  Here in the question the first node is defined so time complexity becomes  F(n-1) = 2(n-1)*(n-1)! = 2*n*(n-1)! – 2*1*(n-1)! = 2*n!-2*(n-1)! = O(n!)

This article is contributed by Shivam Gupta. The explanation for time complexity is contributed by Pranav Nambiar. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above