Sequences of given length where every element is more than or equal to twice of previous
Last Updated :
12 Dec, 2022
Given two integers m & n, find the number of possible sequences of length n such that each of the next element is greater than or equal to twice of the previous element but less than or equal to m.
Examples :
Input : m = 10, n = 4
Output : 4
There should be n elements and value of last
element should be at-most m.
The sequences are {1, 2, 4, 8}, {1, 2, 4, 9},
{1, 2, 4, 10}, {1, 2, 5, 10}
Input : m = 5, n = 2
Output : 6
The sequences are {1, 2}, {1, 3}, {1, 4},
{1, 5}, {2, 4}, {2, 5}
As per the given condition, the n-th value of the sequence can be at most m. There can be two cases for the n-th element:
- If it is m, then the (n-1)th element is at most m/2. We recur for m/2 and n-1.
- If it is not m, then it is at most is m-1. We recur for (m-1) and n.
The total number of sequences is the sum of the number of sequences including m and the number of sequences where m is not included. Thus the original problem of finding number of sequences of length n with max value m can be subdivided into independent subproblems of finding number of sequences of length n with max value m-1 and number of sequences of length n-1 with max value m/2.
C++
#include <iostream>
using namespace std;
int getTotalNumberOfSequences(int m, int n)
{
if (m < n)
return 0;
if (n == 0)
return 1;
return getTotalNumberOfSequences(m - 1, n) +
getTotalNumberOfSequences(m / 2, n - 1);
}
int main()
{
int m = 10;
int n = 4;
cout << "Total number of possible sequences "
<< getTotalNumberOfSequences(m, n);
return 0;
}
|
Java
import java.io.*;
class Sequences {
static int getTotalNumberOfSequences(int m, int n)
{
if (m < n)
return 0;
if (n == 0)
return 1;
return getTotalNumberOfSequences(m - 1, n)
+ getTotalNumberOfSequences(m / 2, n - 1);
}
public static void main(String[] args)
{
int m = 10;
int n = 4;
System.out.println(
"Total number of possible sequences "
+ getTotalNumberOfSequences(m, n));
}
}
|
Python3
def getTotalNumberOfSequences(m,n):
if m<n:
return 0
if n==0:
return 1
res=(getTotalNumberOfSequences(m-1,n)+
getTotalNumberOfSequences(m//2,n-1))
return res
if __name__=='__main__':
m=10
n=4
print('Total number of possible sequences:',getTotalNumberOfSequences(m,n))
|
C#
using System;
class GFG
{
static int getTotalNumberOfSequences(int m, int n)
{
if(m < n)
return 0;
if(n == 0)
return 1;
return getTotalNumberOfSequences (m-1, n) +
getTotalNumberOfSequences (m/2, n-1);
}
public static void Main ()
{
int m = 10;
int n = 4;
Console.Write("Total number of possible sequences " +
getTotalNumberOfSequences(m, n));
}
}
|
PHP
<?php
function getTotalNumberOfSequences($m, $n)
{
if ($m < $n)
return 0;
if ($n == 0)
return 1;
return getTotalNumberOfSequences($m - 1, $n) +
getTotalNumberOfSequences($m / 2, $n - 1);
}
$m = 10;
$n = 4;
echo("Total number of possible sequences ");
echo (getTotalNumberOfSequences($m, $n));
?>
|
Javascript
<script>
function getTotalNumberOfSequences( m, n)
{
if (m < n)
return 0;
if (n == 0)
return 1;
return getTotalNumberOfSequences (m-1, n) +
getTotalNumberOfSequences (m/2, n-1);
}
let m = 10;
let n = 4;
document.write ("Total number of possible sequences ",
getTotalNumberOfSequences(m, n));
</script>
|
Output
Total number of possible sequences 4
Time Complexity: O(2m) in the worst case
Auxiliary Space: O(m), depth of recursion tree is m in the worst case.
Note that the above function computes the same sub-problems again and again. Consider the following tree for f(10, 4).
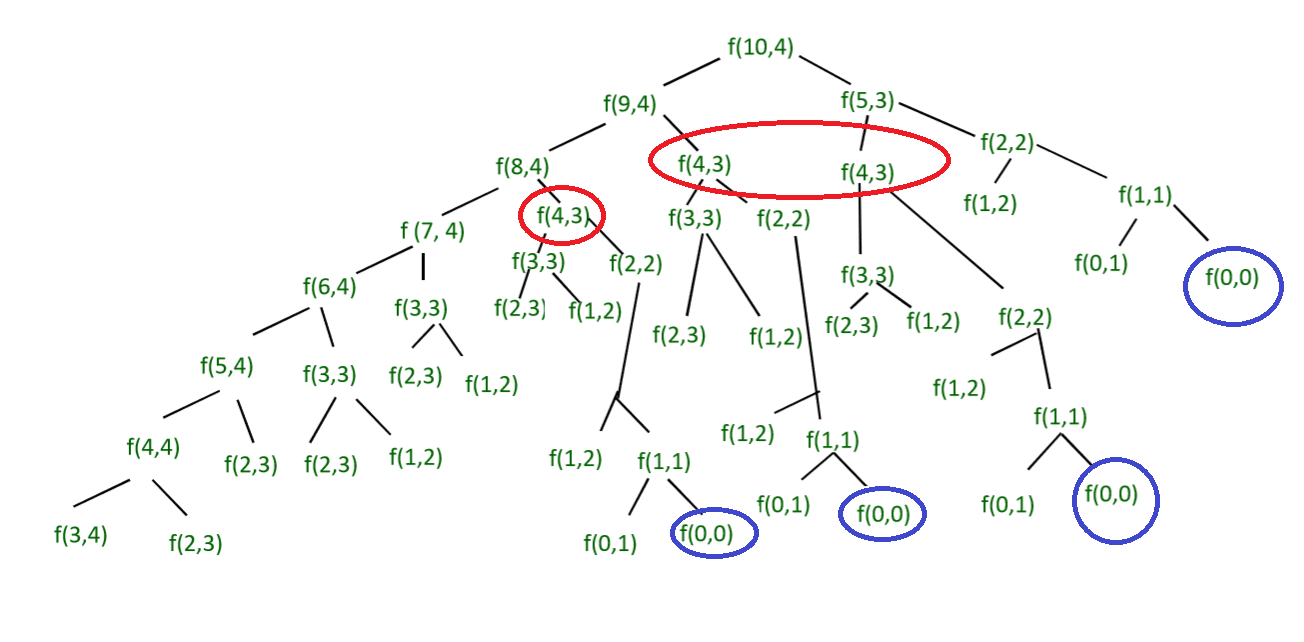
Recursive Tree for m= 10 and N =4
We can solve this problem using dynamic programming.
C++
#include <stdio.h>
int getTotalNumberOfSequences(int m, int n)
{
int T[m+1][n+1];
for (int i=0; i<m+1; i++)
{
for (int j=0; j<n+1; j++)
{
if (i == 0 || j == 0)
T[i][j] = 0;
else if (i < j)
T[i][j] = 0;
else if (j == 1)
T[i][j] = i;
else
T[i][j] = T[i-1][j] + T[i/2][j-1];
}
}
return T[m][n];
}
int main()
{
int m = 10;
int n = 4;
printf("Total number of possible sequences %d",
getTotalNumberOfSequences(m, n));
return 0;
}
|
Java
import java.io.*;
class Sequences {
static int getTotalNumberOfSequences(int m, int n)
{
int T[][] = new int[m + 1][n + 1];
for (int i = 0; i < m + 1; i++) {
for (int j = 0; j < n + 1; j++) {
if (i == 0 || j == 0)
T[i][j] = 0;
else if (i < j)
T[i][j] = 0;
else if (j == 1)
T[i][j] = i;
else
T[i][j] = T[i - 1][j] + T[i / 2][j - 1];
}
}
return T[m][n];
}
public static void main(String[] args)
{
int m = 10;
int n = 4;
System.out.println(
"Total number of possible sequences "
+ getTotalNumberOfSequences(m, n));
}
}
|
Python3
def getTotalNumberOfSequences(m,n):
T=[[0 for i in range(n+1)] for i in range(m+1)]
for i in range(m+1):
for j in range(n+1):
if i==0 or j==0:
T[i][j]=0
elif i<j:
T[i][j]=0
elif j==1:
T[i][j]=i
else:
T[i][j]=T[i-1][j]+T[i//2][j-1]
return T[m][n]
if __name__=='__main__':
m=10
n=4
print('Total number of possible sequences ',getTotalNumberOfSequences(m, n))
|
C#
using System;
class Sequences {
static int getTotalNumberOfSequences(int m, int n)
{
int [,]T=new int[m + 1, n + 1];
for (int i = 0; i < m + 1; i++)
{
for (int j = 0; j < n + 1; j++)
{
if (i == 0 || j == 0)
T[i, j] = 0;
else if (i < j)
T[i,j] = 0;
else if (j == 1)
T[i,j] = i;
else
T[i,j] = T[i - 1, j] + T[i / 2, j - 1];
}
}
return T[m,n];
}
public static void Main ()
{
int m = 10;
int n = 4;
Console.WriteLine("Total number of possible sequences "+
getTotalNumberOfSequences(m, n));
}
}
|
PHP
<?php
function getTotalNumberOfSequences($m, $n)
{
$T = array(array());
for ($i = 0; $i < $m + 1; $i++)
{
for ($j = 0; $j < $n + 1; $j++)
{
if ($i == 0 or $j == 0)
$T[$i][$j] = 0;
else if ($i < $j)
$T[$i][$j] = 0;
else if ($j == 1)
$T[$i][$j] = $i;
else
$T[$i][$j] = $T[$i - 1][$j] +
$T[$i / 2][$j - 1];
}
}
return $T[$m][$n];
}
$m = 10;
$n = 4;
echo "Total number of possible sequences ",
getTotalNumberOfSequences($m, $n);
?>
|
Javascript
<script>
function getTotalNumberOfSequences(m, n)
{
let T = new Array(m+1);
for (let i=0; i<m+1; i++)
{
T[i] = new Array(n+1);
for (let j=0; j<n+1; j++)
{
if (i == 0 || j == 0)
T[i][j] = 0;
else if (i < j)
T[i][j] = 0;
else if (j == 1)
T[i][j] = i;
else
T[i][j] = T[i-1][j] + T[parseInt(i/2, 10)][j-1];
}
}
return T[m][n];
}
let m = 10;
let n = 4;
document.write("Total number of possible sequences "+
getTotalNumberOfSequences(m, n));
</script>
|
Output
Total number of possible sequences 4
Time Complexity : O(m x n)
Auxiliary Space : O(m x n)
Share your thoughts in the comments
Please Login to comment...