Find all reachable nodes from every node present in a given set

Given an undirected graph and a set of vertices, find all reachable nodes from every vertex present in the given set.

Consider below undirected graph with 2 disconnected components. 

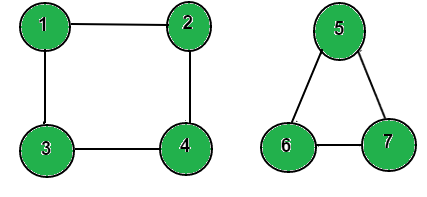
arr[] = {1 , 2 , 5}
Reachable nodes from 1 are  1, 2, 3, 4
Reachable nodes from 2 are 1, 2, 3, 4
Reachable nodes from 5 are 5, 6, 7

Method 1 (Simple)

One straight forward solution is to do a BFS traversal for every node present in the set and then find all the reachable nodes. 

Assume that we need to find reachable nodes for n nodes, the time complexity for this solution would be O(n*(V+E)) where V is number of nodes in the graph and E is number of edges in the graph.

Please note that we need to call BFS as a separate call for every node without using the visited array of previous traversals because a same vertex may need to be printed multiple times. This seems to be an effective solution but consider the case when E = ?(V²) and n = V, time complexity becomes O(V³).

Method 2 (Efficient)

Since the given graph is undirected, all vertices that belong to same component have same set of reachable nodes. So we keep track of vertex and component mappings. Every component in the graph is assigned a number and every vertex in this component is assigned this number. We use the visit array for this purpose, the array which is used to keep track of visited vertices in BFS. 

For a node u, 
if visit[u] is 0 then
    u has not been visited before
else // if not zero then
   visit[u] represents the component number. 

For any two nodes u and v belonging to same 
component, visit[u] is equal to visit[v]

To store the reachable nodes, use a map m with key as component number and value as a vector which stores all the reachable nodes. 

To find reachable nodes for a node u return m[visit[u]]
Look at the pseudo code below in order to understand how to assign component numbers. 

componentNum = 0
for i=1 to n    
    If visit[i] is NOT 0 then
        componentNum++ 
         
        // bfs() returns a list (or vector)
        // for given vertex 'i'
        list = bfs(i, componentNum)
        m[visit[i]]] = list

For the graph shown in the example the visit array would be. 

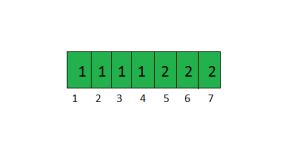
For the nodes 1, 2, 3 and 4 the component number is 1. For nodes 5, 6 and 7 the component number is 2.

Implementation of above idea

C++

// C++ program to find all the reachable nodes
// for every node present in arr[0..n-1].
#include <bits/stdc++.h>
using namespace std;

// This class represents a directed graph using
// adjacency list representation
class Graph
{
public:
    int V;    // No. of vertices

    // Pointer to an array containing adjacency lists
    list<int> *adj;

    Graph(int );  // Constructor

    void addEdge(int, int);

    vector<int> BFS(int, int, int []);
};

Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V+1];
}

void Graph::addEdge(int u, int v)
{
    adj[u].push_back(v); // Add w to v’s list.
    adj[v].push_back(u); // Add v to w’s list.
}

vector<int> Graph::BFS(int componentNum, int src,
                                    int visited[])
{
    // Mark all the vertices as not visited
    // Create a queue for BFS
    queue<int> queue;

    queue.push(src);

    // Assign Component Number
    visited[src] = componentNum;

    // Vector to store all the reachable nodes from 'src'
    vector<int> reachableNodes;

    while(!queue.empty())
    {
        // Dequeue a vertex from queue
        int u = queue.front();
        queue.pop();

        reachableNodes.push_back(u);

        // Get all adjacent vertices of the dequeued
        // vertex u. If a adjacent has not been visited,
        // then mark it visited and enqueue it
        for (auto itr = adj[u].begin();
                itr != adj[u].end(); itr++)
        {
            if (!visited[*itr])
            {
                // Assign Component Number to all the
                // reachable nodes
                visited[*itr] = componentNum;
                queue.push(*itr);
            }
        }
    }
    return reachableNodes;
}

// Display all the Reachable Nodes from a node 'n'
void displayReachableNodes(int n,
            unordered_map <int, vector<int> > m)
{
    vector<int> temp = m[n];
    for (int i=0; i<temp.size(); i++)
        cout << temp[i] << " ";

    cout << endl;
}

// Find all the reachable nodes for every element
// in the arr
void findReachableNodes(Graph g, int arr[], int n)
{
    // Get the number of nodes in the graph
    int V = g.V;

    // Take a integer visited array and initialize
    // all the elements with 0
    int visited[V+1];
    memset(visited, 0, sizeof(visited));

    // Map to store list of reachable Nodes for a
    // given node.
    unordered_map <int, vector<int> > m;

    // Initialize component Number with 0
    int componentNum = 0;

    // For each node in arr[] find reachable
    // Nodes
    for (int i = 0 ; i < n ; i++)
    {
        int u = arr[i];

        // Visit all the nodes of the component
        if (!visited[u])
        {
            componentNum++;

            // Store the reachable Nodes corresponding to
            // the node 'i'
            m[visited[u]] = g.BFS(componentNum, u, visited);
        }

        // At this point, we have all reachable nodes
        // from u, print them by doing a look up in map m.
        cout << "Reachable Nodes from " << u <<" are\n";
        displayReachableNodes(visited[u], m);
    }
}

// Driver program to test above functions
int main()
{
    // Create a graph given in the above diagram
    int V = 7;
    Graph g(V);
    g.addEdge(1, 2);
    g.addEdge(2, 3);
    g.addEdge(3, 4);
    g.addEdge(3, 1);
    g.addEdge(5, 6);
    g.addEdge(5, 7);

    // For every ith element in the arr
    // find all reachable nodes from query[i]
    int arr[] = {2, 4, 5};

    // Find number of elements in Set
    int n = sizeof(arr)/sizeof(int);

    findReachableNodes(g, arr, n);

    return 0;
}

Python3

# Python3 program to find all the reachable nodes
# for every node present in arr[0..n-1]
from collections import deque

def addEdge(v, w):

    global visited, adj
    adj[v].append(w)
    adj[w].append(v)

def BFS(componentNum, src):

    global visited, adj

    # Mark all the vertices as not visited
    # Create a queue for BFS
    #a =  visited
    queue = deque()

    queue.append(src)

    # Assign Component Number
    visited[src] = 1

    # Vector to store all the reachable
    # nodes from 'src'
    reachableNodes = []
    #print("0:",visited)

    while (len(queue) > 0):

        # Dequeue a vertex from queue
        u = queue.popleft()

        reachableNodes.append(u)

        # Get all adjacent vertices of the dequeued
        # vertex u. If a adjacent has not been visited,
        # then mark it visited and enqueue it
        for itr in adj[u]:
            if (visited[itr] == 0):

                # Assign Component Number to all the
                # reachable nodes
                visited[itr] = 1
                queue.append(itr)

    return reachableNodes

# Display all the Reachable Nodes
# from a node 'n'
def displayReachableNodes(m):

    for i in m:
        print(i, end = " ")

    print()

def findReachableNodes(arr, n):

    global V, adj, visited

    # Get the number of nodes in the graph

    # Map to store list of reachable Nodes for a
    # given node.
    a = []

    # Initialize component Number with 0
    componentNum = 0

    # For each node in arr[] find reachable
    # Nodes
    for i in range(n):
        u = arr[i]

        # Visit all the nodes of the component
        if (visited[u] == 0):
            componentNum += 1

            # Store the reachable Nodes corresponding
            # to the node 'i'
            a = BFS(componentNum, u)

        # At this point, we have all reachable nodes
        # from u, print them by doing a look up in map m.
        print("Reachable Nodes from ", u, " are")
        displayReachableNodes(a)

# Driver code
if __name__ == '__main__':

    V = 7
    adj = [[] for i in range(V + 1)]
    visited = [0 for i in range(V + 1)]
    addEdge(1, 2)
    addEdge(2, 3)
    addEdge(3, 4)
    addEdge(3, 1)
    addEdge(5, 6)
    addEdge(5, 7)

    # For every ith element in the arr
    # find all reachable nodes from query[i]
    arr = [ 2, 4, 5 ]

    # Find number of elements in Set
    n = len(arr)

    findReachableNodes(arr, n)

# This code is contributed by mohit kumar 29

Java

// Java Code //

import java.util.*;

public class ReachableNodes {
    private static int V;
    private static List<List<Integer> > adj;
    private static boolean[] visited;
    public static void addEdge(int v, int w)
    {
        adj.get(v).add(w);
        adj.get(w).add(v);
    }
    public static List<Integer> BFS(int componentNum,
                                    int src)
    {
        List<Integer> queue = new ArrayList<>();
        queue.add(src);
        visited[src] = true;
        List<Integer> reachableNodes = new ArrayList<>();
        while (!queue.isEmpty()) {
            int u = queue.remove(0);
            reachableNodes.add(u);
            for (int itr : adj.get(u)) {
                if (visited[itr] == false) {
                    visited[itr] = true;
                    queue.add(itr);
                }
            }
        }
        return reachableNodes;
    }
    public static void
    displayReachableNodes(List<Integer> m)
    {
        for (int i : m) {
            System.out.print(i + " ");
        }
        System.out.println();
    }
    public static void findReachableNodes(int[] arr, int n)
    {
        List<Integer> a = new ArrayList<>();
        int componentNum = 0;
        for (int i = 0; i < n; i++) {
            int u = arr[i];
            if (visited[u] == false) {
                componentNum++;
                a = BFS(componentNum, u);
            }
            System.out.println("Reachable Nodes from " + u
                               + " are");
            displayReachableNodes(a);
        }
    }
    public static void main(String[] args)
    {
        V = 7;
        adj = new ArrayList<>();
        for (int i = 0; i < V + 1; i++) {
            adj.add(new ArrayList<>());
        }
        visited = new boolean[V + 1];
        addEdge(1, 2);
        addEdge(2, 3);
        addEdge(3, 4);
        addEdge(3, 1);
        addEdge(5, 6);
        addEdge(5, 7);
        int[] arr = { 2, 4, 5 };
        int n = arr.length;
        findReachableNodes(arr, n);
    }
}

C#

// C# program to find all the reachable nodes
// for every node present in arr[0..n-1].

using System;
using System.Collections.Generic;
// This class represents a directed graph using
// adjacency list representation
public class ReachableNodes {
    private static int V; // No. of vertices

    // Pointer to an array containing adjacency lists
    private static List<List<int> > adj;
    private static bool[] visited;

    public static void AddEdge(int v, int w)
    {
        adj[v].Add(w); // Add w to v’s list.
        adj[w].Add(v); // Add v to w’s list.
    }

    public static List<int> BFS(int componentNum, int src)
    {
        // Mark all the vertices as not visited
        // Create a queue for BFS
        List<int> queue = new List<int>();
        queue.Add(src);
        // Assign Component Number
        visited[src] = true;
        // Vector to store all the reachable nodes from
        // 'src'
        List<int> reachableNodes = new List<int>();

        while (queue.Count > 0) {

            // Dequeue a vertex from queue
            int u = queue[0];
            queue.RemoveAt(0);
            reachableNodes.Add(u);
            // Get all adjacent vertices of the dequeued
            // vertex u. If a adjacent has not been visited,
            // then mark it visited and enqueue it
            foreach(int itr in adj[u])
            {
                if (visited[itr] == false) {
                    // Assign Component Number to all the
                    // reachable nodes
                    visited[itr] = true;
                    queue.Add(itr);
                }
            }
        }

        return reachableNodes;
    }

    // Display all the Reachable Nodes from a node 'n'
    public static void DisplayReachableNodes(List<int> m)
    {
        foreach(int i in m) { Console.Write(i + " "); }
        Console.WriteLine();
    }
    // Find all the reachable nodes for every element
    // in the arr
    public static void FindReachableNodes(int[] arr, int n)
    {

        List<int> a = new List<int>();
        // Initialize component Number with 0
        int componentNum = 0;
        // For each node in arr[] find reachable
        // Nodes
        for (int i = 0; i < n; i++) {
            int u = arr[i];

            if (visited[u]
                == false) { // Store the reachable Nodes
                            // corresponding to
                // the node 'i'
                componentNum++;
                a = BFS(componentNum, u);
            }
            // At this point, we have all reachable nodes
            // from u, print them by doing a look up in map
            // m.
            Console.WriteLine("Reachable Nodes from " + u
                              + " are");
            DisplayReachableNodes(a);
        }
    }
    // Driver code
    public static void Main(string[] args)
    { // Create a graph given in the above diagram
        V = 7;
        adj = new List<List<int> >();

        for (int i = 0; i < V + 1; i++) {
            adj.Add(new List<int>());
        }

        visited = new bool[V + 1];

        AddEdge(1, 2);
        AddEdge(2, 3);
        AddEdge(3, 4);
        AddEdge(3, 1);
        AddEdge(5, 6);
        AddEdge(5, 7);
        // For every ith element in the arr
        // find all reachable nodes from query[i]
        int[] arr = { 2, 4, 5 };
        // Find number of elements in Set
        int n = arr.Length;

        FindReachableNodes(arr, n);
    }
}

Javascript

// This function adds an edge between two vertices
function addEdge(v, w) {
adj[v].push(w);
adj[w].push(v);
}

// This function performs BFS on a connected component starting at a source vertex and returns the reachable nodes
function BFS(componentNum, src) {
let queue = [];
queue.push(src);
visited[src] = true;
let reachableNodes = [];
while (queue.length != 0) {
let u = queue.shift();
reachableNodes.push(u);
for (let itr of adj[u]) {
if (visited[itr] == false) {
visited[itr] = true;
queue.push(itr);
}
}
}
return reachableNodes;
}

// This function displays the reachable nodes from a source vertex
function displayReachableNodes(m) {
for (let i of m) {
console.log(i + " ");
}
console.log();
}

// This function finds the reachable nodes from each vertex in the array arr
function findReachableNodes(arr, n) {
let a = [];
let componentNum = 0;
for (let i = 0; i < n; i++) {
let u = arr[i];
if (visited[u] == false) {
componentNum++;
a = BFS(componentNum, u);
}
console.log("Reachable Nodes from " + u + " are");
displayReachableNodes(a);
}
}

// Main function
let V = 7;
let adj = new Array(V + 1);
for (let i = 0; i < V + 1; i++) {
adj[i] = new Array();
}
let visited = new Array(V + 1).fill(false);
addEdge(1, 2);
addEdge(2, 3);
addEdge(3, 4);
addEdge(3, 1);
addEdge(5, 6);
addEdge(5, 7);
let arr = [2, 4, 5];
let n = arr.length;
findReachableNodes(arr, n);

Output

Reachable Nodes from 2 are
2 1 3 4 
Reachable Nodes from 4 are
2 1 3 4 
Reachable Nodes from 5 are
5 6 7 

Time Complexity Analysis:

n = Size of the given set 
E = Number of Edges 
V = Number of Nodes 
O(V+E) for BFS 
In worst case all the V nodes are displayed for each node present in the given, i.e only one component in the graph so it takes O(n*V) time.

Worst Case Time Complexity : O(V+E) + O(n*V)

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.