Count the number of non-reachable nodes

Given an undirected graph and a set of vertices, we have to count the number of non-reachable nodes from the given head node using a depth-first search.

Consider below undirected graph with two disconnected components:

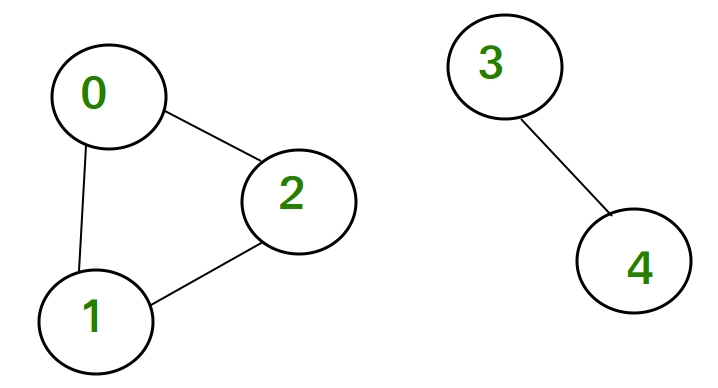
In this graph, if we consider 0 as a head node, then the node 0, 1 and 2 are reachable. We mark all the reachable nodes as visited. All those nodes which are not marked as visited i.e, node 3 and 4 are non-reachable nodes. Hence their count is 2.

Example:

Input :   5
          0 1
          0 2
          1 2
          3 4
Output : 2

We can either use BFS or DFS for this purpose. In the below implementation, DFS is used. We do DFS from a given source. Since the given graph is undirected, all the vertices that belong to the disconnected component are non-reachable nodes. We use the visited array for this purpose, the array which is used to keep track of non-visited vertices in DFS. In DFS, if we start from the head node it will mark all the nodes connected to the head node as visited. Then after traversing the graph, we count the number of nodes that are not marked as visited from the head node.

Implementation:

C++

// C++ program to count non-reachable nodes
// from a given source using DFS.
#include <iostream>
#include <list>
using namespace std;

// Graph class represents a directed graph
// using adjacency list representation
class Graph {
    int V; // No. of vertices

    // Pointer to an array containing
    // adjacency lists
    list<int>* adj;

    // A recursive function used by DFS
    void DFSUtil(int v, bool visited[]);

public:
    Graph(int V); // Constructor

    // function to add an edge to graph
    void addEdge(int v, int w);

    // DFS traversal of the vertices
    // reachable from v
    int countNotReach(int v);
};

Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
}

void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w); // Add w to v’s list.
    adj[w].push_back(v); // Add v to w's list.
}

void Graph::DFSUtil(int v, bool visited[])
{
    // Mark the current node as visited and
    // print it
    visited[v] = true;

    // Recur for all the vertices adjacent
    // to this vertex
    list<int>::iterator i;
    for (i = adj[v].begin(); i != adj[v].end(); ++i)
        if (!visited[*i])
            DFSUtil(*i, visited);
}

// Returns count of not reachable nodes from
// vertex v.
// It uses recursive DFSUtil()
int Graph::countNotReach(int v)
{
    // Mark all the vertices as not visited
    bool* visited = new bool[V];
    for (int i = 0; i < V; i++)
        visited[i] = false;

    // Call the recursive helper function
    // to print DFS traversal
    DFSUtil(v, visited);

    // Return count of not visited nodes
    int count = 0;
    for (int i = 0; i < V; i++) {
        if (visited[i] == false)
            count++;
    }
    return count;
}

int main()
{
    // Create a graph given in the above diagram
    Graph g(8);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(3, 4);
    g.addEdge(4, 5);
    g.addEdge(6, 7);

    cout << g.countNotReach(2);

    return 0;
}

Java

// Java program to count non-reachable nodes
// from a given source using DFS.
import java.util.*;

// Graph class represents a directed graph
// using adjacency list representation
@SuppressWarnings("unchecked")
class Graph{

// No. of vertices
public int V;

// Pointer to an array containing
// adjacency lists
public ArrayList []adj;

public Graph(int V)
{
    this.V = V;
    adj = new ArrayList[V];
    for(int i = 0; i < V; i++)
    {
        adj[i] = new ArrayList();
    }
}

void addEdge(int v, int w)
{

    // add w to v’s list.
    adj[v].add(w);

    // add v to w's list.
    adj[w].add(v);
}

void DFSUtil(int v, boolean []visited)
{

    // Mark the current node as visited and
    // print it
    visited[v] = true;

    // Recur for all the vertices adjacent
    // to this vertex
    for(int i : (ArrayList<Integer>)adj[v])
    {
        if (!visited[i])
            DFSUtil(i, visited);
    }
}

// Returns count of not reachable nodes from
// vertex v.
// It uses recursive DFSUtil()
int countNotReach(int v)
{

    // Mark all the vertices as not visited
    boolean []visited = new boolean[V];

    for(int i = 0; i < V; i++)
        visited[i] = false;

    // Call the recursive helper function
    // to print DFS traversal
    DFSUtil(v, visited);

    // Return count of not visited nodes
    int count = 0;
    for(int i = 0; i < V; i++)
    {
        if (visited[i] == false)
            count++;
    }
    return count;
}

// Driver Code
public static void main(String []args)
{

    // Create a graph given in the above diagram
    Graph g = new Graph(8);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(3, 4);
    g.addEdge(4, 5);
    g.addEdge(6, 7);

    System.out.print(g.countNotReach(2));
}
}

// This code is contributed by Pratham76

Python3

# Python3 program to count non-reachable
# nodes from a given source using DFS.

# Graph class represents a directed graph
# using adjacency list representation
class Graph:
    def __init__(self, V):
        self.V = V
        self.adj = [[] for i in range(V)]

    def addEdge(self, v, w):
        self.adj[v].append(w) # Add w to v’s list.
        self.adj[w].append(v) # Add v to w's list.

    def DFSUtil(self, v, visited):

        # Mark the current node as
        # visited and print it
        visited[v] = True

        # Recur for all the vertices
        # adjacent to this vertex
        i = self.adj[v][0]
        for i in self.adj[v]:
            if (not visited[i]):
                self.DFSUtil(i, visited)

    # Returns count of not reachable
    # nodes from vertex v.
    # It uses recursive DFSUtil()
    def countNotReach(self, v):

        # Mark all the vertices as not visited
        visited = [False] * self.V

        # Call the recursive helper
        # function to print DFS traversal
        self.DFSUtil(v, visited)

        # Return count of not visited nodes
        count = 0
        for i in range(self.V):
            if (visited[i] == False):
                count += 1
        return count

# Driver Code
if __name__ == '__main__':

    # Create a graph given in the
    # above diagram
    g = Graph(8)
    g.addEdge(0, 1)
    g.addEdge(0, 2)
    g.addEdge(1, 2)
    g.addEdge(3, 4)
    g.addEdge(4, 5)
    g.addEdge(6, 7)

    print(g.countNotReach(2))

# This code is contributed by PranchalK

C#

// C# program to count non-reachable nodes
// from a given source using DFS.
using System;
using System.Collections;
using System.Collections.Generic;

// Graph class represents a directed graph
// using adjacency list representation
class Graph{

// No. of vertices
public int V;

// Pointer to an array containing
// adjacency lists
public ArrayList []adj;

public Graph(int V)
{
    this.V = V;
    adj = new ArrayList[V];
    for(int i = 0; i < V; i++)
    {
        adj[i] = new ArrayList();
    }
}

void addEdge(int v, int w)
{

    // Add w to v’s list.
    adj[v].Add(w);

    // Add v to w's list.
    adj[w].Add(v);
}

void DFSUtil(int v, bool []visited)
{

    // Mark the current node as visited and
    // print it
    visited[v] = true;

    // Recur for all the vertices adjacent
    // to this vertex
    foreach(int i in (ArrayList)adj[v])
    {
        if (!visited[i])
            DFSUtil(i, visited);
    }
}

// Returns count of not reachable nodes from
// vertex v.
// It uses recursive DFSUtil()
int countNotReach(int v)
{

    // Mark all the vertices as not visited
    bool []visited = new bool[V];

    for(int i = 0; i < V; i++)
        visited[i] = false;

    // Call the recursive helper function
    // to print DFS traversal
    DFSUtil(v, visited);

    // Return count of not visited nodes
    int count = 0;
    for(int i = 0; i < V; i++)
    {
        if (visited[i] == false)
            count++;
    }
    return count;
}

// Driver Code
static void Main(string []args)
{

    // Create a graph given in the above diagram
    Graph g = new Graph(8);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(3, 4);
    g.addEdge(4, 5);
    g.addEdge(6, 7);

    Console.Write(g.countNotReach(2));
}
}

// This code is contributed by rutvik_56

Javascript

<script>
    // Javascript program to count non-reachable nodes
    // from a given source using DFS.

    // Graph class represents a directed graph
    // using adjacency list representation
    let V = 8;
    let adj = [];
    for(let i = 0; i < V; i++)
    {
      adj.push([]);
    }

    function addEdge(v, w)
    {

        // Add w to v’s list.
        adj[v].push(w);

        // Add v to w's list.
        adj[w].push(v);
    }

    function DFSUtil(v, visited)
    {

        // Mark the current node as visited and
        // print it
        visited[v] = true;

        // Recur for all the vertices adjacent
        // to this vertex
        for(let i = 0; i < adj[v].length; i++)
        {
            if (!visited[adj[v][i]])
                DFSUtil(adj[v][i], visited);
        }
    }

    // Returns count of not reachable nodes from
    // vertex v.
    // It uses recursive DFSUtil()
    function countNotReach(v)
    {

        // Mark all the vertices as not visited
        let visited = new Array(V);

        for(let i = 0; i < V; i++)
            visited[i] = false;

        // Call the recursive helper function
        // to print DFS traversal
        DFSUtil(v, visited);

        // Return count of not visited nodes
        let count = 0;
        for(let i = 0; i < V; i++)
        {
            if (visited[i] == false)
                count++;
        }
        return count;
    }

    // Create a graph given in the above diagram
    addEdge(0, 1);
    addEdge(0, 2);
    addEdge(1, 2);
    addEdge(3, 4);
    addEdge(4, 5);
    addEdge(6, 7);

    document.write(countNotReach(2));

    // This code is contributed by suresh07.
</script>

Output

5