Oscillatory and Periodic Motion
Last Updated :
14 Jul, 2021
There are many types of motions that are encountered in daily life- rectilinear motion and the motion of a projectile is one such example. Both of these motions are non-repetitive. It means that the object does not come back to the same place again. There are some motions that are repetitive in nature. For example, planetary motion. All the planets move around the sun and complete revolutions each year. This type of motion is periodic motion. The study of periodic motion is a big part of physics, and it is essential to know how to analyze such motions. Let’s see these motions in detail.
Periodic and Oscillatory Motions
Consider the motion of an insect trying to climb a wall. The insect is trying to climb a vertical wall, it reaches some height and falls back again. The insect falls back but again tries to climb the wall. The graph of the height of the insect with time is shown below. In such a graph, notice that the insect comes back to zero again and again. This kind of graph can also be observed in a bouncing ball. The ball also comes back to its position on the ground again and again.

In the above graph, the motion repeats itself after a certain period of time. This kind of motion is called periodic motion. Now, since the object is changing its velocity, that means there must be a force that is acting on the object which brings it back to a certain position. That certain position is called mean position. When the body is in this position, no force is acting on it. So, this position is called the equilibrium position.
The force that tries to bring the body to an equilibrium position gives rise to the repetitive behavior in the motion. This repetitive behavior is also called oscillations or vibrations.
Note: There is not really much difference between the oscillations and vibrations. When the frequency is small, they are called oscillations. Else, they are called vibrations.
Periodic Motion
Consider the motion of the clock, the hour hands, second hands, and minute hands. These hands cover the whole clock and come back to the same position. In periodic motion, a body starts from its equilibrium position and returns to it at equal intervals of time. Circular motion is an example of periodic motion.
Periodic motion is different from oscillatory motion. For example, circular motion is a periodic motion but it is not an oscillatory motion. Some examples of periodic motion are given below –
- A rocking chair
- A bouncing ball
- Circular Motion
Oscillatory Motion
Oscillatory motion is the motion of objects back and forth around an equilibrium position. A swinging pendulum is an example of oscillatory motion. In practice, the bodies making oscillator motion eventually come to rest due to damping caused by external forces such as friction or air pressure. But this kind of motion can be kept by using an external force that maintains an equal time interval. Some examples of oscillatory motion are given below:
- Mass performing oscillations attached to a spring.
- A tuning fork performing vibrations.
- A simple pendulum.
Simple Harmonic Motion is the simplest kind of oscillatory motion.
Simple Harmonic Motion (SHM) is a kind of oscillatory motion where the net force on the system is restoring force which brings it back to an equilibrium position. If the restoring force is given by F, and the displacement from the mean position is x
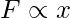
Period and Frequency
Since oscillatory and periodic motion repeat themselves after equal intervals of time. There are certain measurable quantities that allow us to describe any such motion mathematically. Such quantities also allow us to describe the state of any object in periodic motion.
The smallest interval after a body repeats its motion is called its Time Period. It is denoted by T. Its SI unit is seconds. The reciprocal of the time period (T) is called frequency. It is denoted by f or v and its SI unit is Hz. It denotes the number of repetitions per second.
v = 1 / T
A displacement can be defined as the distance of the oscillating body from the equilibrium position.
A simple periodic function can be written as,
f(t) = Asin(ωt)
The argument ωt is given by,
T = 2π / ω
Thus, the function f(t) is periodic with T,
f(t + T) = f(t)
Sample Problems
Problem 1: Find out the frequency of a body in HM if the time period for the body is 0.1 seconds.
Solution:
The frequency of a body is given by,
v = 1 / T
where v = frequency and T = time period.
Given: T = 0.1 s
Plugging the value into the equation,
v = 1 / 0.1 s
= 10 Hz.
Problem 2: Find out the time period of a body in SHM if the frequency for the body is 250Hz.
Solution:
The frequency of a body is given by,
v = 1 / T
where, v = frequency and T = time period.
Given: v = 250 Hz
Plugging the value into the equation,
v = 1 / T
250 Hz = 1 / T
or
T = 0.004 s
Problem 3: A person’s heartbeat when measured came out to be 80 beats per minute. Find the time period and frequency.
Solution:
The frequency of a body is given by the number of times heart beats per second.
v = 80 / 60
v = 1.33 beats per second
The frequency is given by,
v = 1 / T
where v = frequency and T = time period.
Given: v = 1.33 Hz
Plugging the value into the equation,
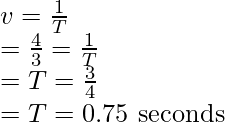
Problem 4: A body performing SHM is governed by the following equation: A = 5sin(44t). Find the time period.
Solution:
A standard equation of an SHM is given by,
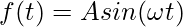
where T = 2π / ω
In this case, A = 5sin(44t)
Comparing the two equations, we find that
ω = 44
Plugging the value into the equation for a time period.
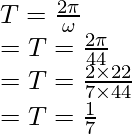
Problem 5: A body performing SHM is governed by the following equation: A = 3sin(t). Find the time period.
Solution:
A standard equation of an SHM is given by,
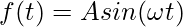
Here, 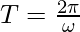
In this case, A = 3sin(t)
Comparing the two equations, we find that
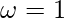
Plugging the value into the equation for a time period.
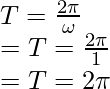
Problem 6: A body performing SHM is governed by the following equation: A = sin(t) + cos(t). Find the time period.
Solution:
A standard equation of an SHM is given by,
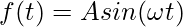
Here, 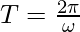
In this case, A = sin(t) + cos(t)
This equation can be rewritten as,
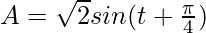
Comparing the two equations, we find that
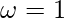
Plugging the value into the equation for a time period.
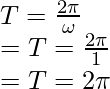
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...