Electric Field due to Infinitely Long Straight Wire
Last Updated :
05 Aug, 2021
Gauss law is a very important part of electromagnetism and physics. It is used to relate the distribution of charge with the resulting electric field due to the charge. This law was formulated by Joseph Lagrange in 1773, followed by Carl Gauss in 1813. Both of them formulated this law in the context of the attraction of ellipsoids. This law is also included in one of Maxwell’s four equations which form the basis for classical electrodynamics. Let’s study this concept in detail.
Gauss’s Law
The electric flux through an area is defined as the product of the electric field with the area of surface projected perpendicular to the electric field. In general, for gauss’ law, closed surfaces are assumed. This law is an important tool since it allows the estimation of the electric charge enclosed inside a closed surface. This law can be used to simplify the calculation for the geometries which have symmetry between them.
Electric Flux
Consider a surface dS and a liquid flowing along the surface with a velocity “v”. The rate of flow of liquid through the surface is given by, “vdS”. This is said to be the flux of the liquid flowing through the surface. In a similar manner, the flow of the electric field is defined. It is defined as the electric field flowing through a small area patch “dS”. The number of electric field lines passing through the patch is proportional to,
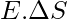
If the area is tilted by an angle θ, it becomes,
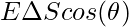
The flux is denoted by 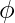 ,
,
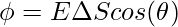
Gauss’s Law
Consider a small charge “q” kept inside a sphere of the radius r. This sphere can be divided into smaller area elements as shown in the figure below. The electric field passing through that element will be given as,
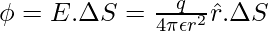

The total flux can be calculated by adding flux through individual elements,
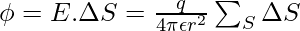
Now, the total area of the sphere will be 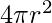
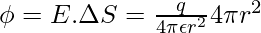
⇒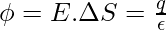
This is the general result of Gauss’ law.
The total flux along a closed surface S, enclosing a charge q is,
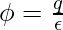
Electric Field due to Infinitely Long Straight Wire
Gauss’s law can be used to derive the equations for an electrical field through a variety of charged shapes. Consider an infinitely long wire containing the charge. The charge per unit length of that wire is given by 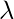 . The wire has an axis of symmetry that is shown in the figure below. The goal is to derive the equation for calculating the electric field produced by this wire.
. The wire has an axis of symmetry that is shown in the figure below. The goal is to derive the equation for calculating the electric field produced by this wire.

Suppose a radial vector OP is taken and it is rotated around the wire. This means that the electric field must have the same value at all the points P, P’ and P”. The direction of the electric field is radially outwards if the charge is positive and vice-versa.

To calculate the electric field, imagine a cylindrical Gaussian surface. Since the field is radial everywhere, flux along the two faces of the cylinders is zero. On the cylindrical part of the surface, E is perpendicular to the surface at each point and its magnitude is constant since it depends only on r. The surface area of the curved part is 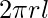 where l is the length of the cylinder.
where l is the length of the cylinder.
Flux through the surface = flux through the curved part of the cylinder
= E x 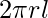
The surface encloses a charge equal to 
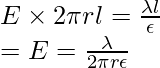
Let’s look at some sample problems.
Sample Problems
Question 1: In Gauss’ law, the point charge inside the closed surface must be distributed in,
- Sequentially
- Rational
- In Line
- Arbitrary.
Answer:
According to gauss’s law, the flux coming out of the enclosed shell only depends on the quantity of charge enclosed inside the shell.
It can be distributed arbitrary.
Thus, answer (4).
Question 2: The flux going through a hexagonal prism is 2 x 103 N.m2/C. What is the charge inside the hexagonal prism?
Answer:
According to Gauss’s law, the flux and charges are related by the following equation:
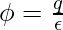
Given: ∅ = 2 x 103 N.m2/C
plugging this value into the equation,
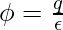
⇒ 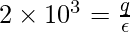
⇒ 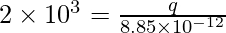
⇒ q = 1.77 × 10-8 C
Question 3: The flux going into a cube-shaped surface is 1 x 103 N.m2/C and the flux coming out 4 x 103N.m2/C. What is the charge inside the hexagonal prism?

Answer:
According to Gauss’s law, the flux and charges are related by the following equation:
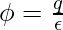
Given: ∅in = 4 x 103 N.m2/C and ∅out = 1 x 103 N.m2/C
∅net =∅out – ∅in = 3 x 103 N.m2/C
plugging this value into the equation,
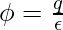
⇒ 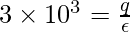
⇒ 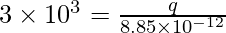
⇒ q = 2.665 × 10-8 C
Question 4: Find the electric field at 5m from an infinitely long wire with a linear charge density of 5 x 10-3C/m.
Answer:
The electric field due to an infinite charge carrying conductor is given by,
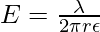
Given: r = 5m and 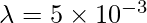
plugging the values into the equation,
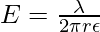
⇒ 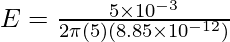
⇒ E = 18 × 109 × 10-3
⇒ E = 18 × 106
Question 5: Find the electric field at 1m from an infinitely long wire with a linear charge density of 2 x 10-3C/m.
Answer:
The electric field due to an infinite charge carrying conductor is given by,
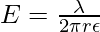
Given: r = 1m and 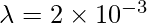
plugging the values into the equation,
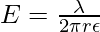
⇒ 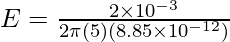
⇒ E = 18 x 109 x 2 x 10-3
⇒ E = 36 x 106 N/C
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...