An electric dipole is defined as a pair of equal and opposite electric charges that are separated, by a small distance. An example of an electric dipole includes two atoms separated by small distances. The magnitude of the electric dipole is obtained by taking the product of either of the charge and the distance between them. In this article, we will learn about electric dipole its application, and others in detail.
What is Electric Dipole?
A pair of equal and opposite point charges q and –q separated by a distance 2a form an electric dipole and the electric dipole moment (p) is the product of the charge and the space between the charges (2a). It is used to determine the strength of an electric dipole.
As we know that Electric Dipole is a vector quantity i.e. it has both magnitude and direction. The magnitude of the electric dipole is the product of either of the electric charge and the distance between them. The direction of the electric dipole is from negative charge to positive charge.
Visualising Electric Dipole
Let’s take two charges +q and -q equal in magnitude but opposite in direction, and the distance between them is d. Then this system is called the electric dipole.
An electric dipole is denoted by the symbol “p”. It is a Vector quantity. In the image given below two point charges +q and -q are separated by distance ‘d’ and hence the electric dipole moment is p = q×d
Magnitude and Dimension of an Electric Dipole
An electric dipole is a vector quantity and its magnitude is given as,
|p| = q×d
It is clear that the magnitude of the electric dipole is the product of either charge with the distance between them.
Electric Dipole is measured in Coulomb-meter. Its dimensional formula is [M0 L1 T1 I1]
Direction of Electric Dipole Moment
Electric dipole moment is a vector quantity and hence it has a unique direction. The direction of the electric dipole is from negative charge to positive charge. The Axis of the electric dipole moment is the line that joins both charges.
Note: It is important to note that the direction of Electric Dipole Moment is taken from negative end to positive end in physics. In Chemistry, the direction of Electric Dipole Moment is taken to be opposite i.e. from positive charge to negative charge.
Electric Potential due to a Dipole (V)
Let’s take two charges -q and +q placed at A and B respectively. The distance between them AB is d they form a dipole as p = qd the centre of AB is Q. Now, if any point P which makes an angle θ with the AB and QP is r then the electric potential at P by the electric dipole is given by,
V = 1 / 4πεo × [p cos(θ) / r2]
When θ = 0°
Then,
cos θ = cos 0° = 1
Now,
V = 1 / 4πεo × [p cos(θ) / r2]
V = 1 / 4πεo × [p cos(0°) / r2]
V = 1 / 4πεo × [p / r2]
When θ = 90°
Then,
cos θ = cos 90° = 0
Now,
V = 1 / 4πεo × [p cos(θ) / r2]
V = 1 / 4πεo × [p cos(90°) / r2]
V = 0
Also Check:
Electric Field of an Electric Dipole
Coulomb’s law and the superposition principle may be used to calculate the electric field of a pair of charges (–q and q) at any point in space. For the following two scenarios, the results are simple and clear,
- When the point is on the dipole axis,
- When it is on the equatorial plane of the dipole, i.e. on a plane perpendicular to the dipole axis through its centre.
By applying the parallelogram law of vectors, the electric field at any general point P is determined by summing the electric fields E–q due to the charge –q and E+q due to the charge q.
For Points on Axis
Suppose the point P be at distance r from the centre of the dipole on the side of the charge q. Then electric field E–q due to the charge –q can be expressed as,
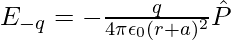
where
 is the unit vector along the dipole axis that is from –q to q.
is the unit vector along the dipole axis that is from –q to q.
Similarly, Then electric field E+q due to the charge +q can be expressed as,
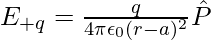
Now, the total field at P can be calculated by adding the electric fields E–q due to the charge –q and E+q due to the charge +q and can be expressed as,
![Rendered by QuickLaTeX.com E=E_{+q}+E_{-q}\\ E=\frac{q}{4\pi\epsilon_0(r-a)^2}\hat{P}+\left(-\frac{q}{4\pi\epsilon_0(r+a)^2}\hat{P}\right)\\ E=\frac{q}{4\pi\epsilon_0(r-a)^2}\hat{P}-\frac{q}{4\pi\epsilon_0(r+a)^2}\hat{P}\\ E=\frac{q}{4\pi\epsilon_0}\left[\frac{1}{(r-a)^2}-\frac{1}{(r+a)^2}\right]\hat{P}\\ E=\frac{q}{4\pi\epsilon_0}\frac{4ar}{(r^2-a^2)^2}\hat{P}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9c3846a45b833a56d1b90015bd383c19_l3.png)
For r >> a the above expression can be written as,
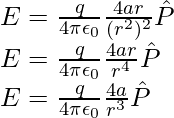
For Points on Equatorial Plane
Then, the electric field E+q due to the charge +q can be expressed as,
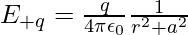
Similarly, then the electric field E-q due to the charge –q can be expressed as,
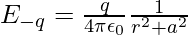
It is observed that the electric fields E–q due to the charge –q and E+q due to the charge +q are equal. The E+q and E–q directions are displayed in the above-given figure. The components normal to the dipole axis clearly cancel out. Along the dipole axis, the components add up. The entire electric field is in the opposite direction of  .
.
The above expression can be added as,
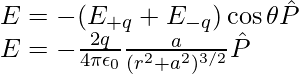
At large distances (r >> a), the above expression can be written as,
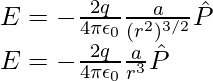
At great distances, it is evident in both cases that the dipole field does not involve q and a separately; it is dependent on the product qa. This hints at the meaning of the dipole moment. The dipole moment of an electric dipole is a vector quantity and it is symbol is p is defined by
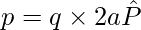
The electric field of a dipole at large distances (r >> a) assumes simple shapes in terms of p:
- At a point on the dipole axis:
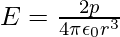
- At a point on the equatorial plane:
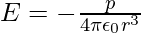
It’s worth noting that the dipole field at great distances decreases off as 1/r3 rather than 1/r2. Furthermore, the dipole field’s amplitude and direction are dependent not only on the distance r but also on the angle formed by the position vector r and the dipole moment p.
Dipole in an External Electric Field
The image given below shows an electric dipole kept in an electric field and torque applied to it.
.png)
Suppose a permanent dipole in a uniform external field E with a dipole moment of p. On q, there is a force qE and on –q, there is a force –qE. Because E is uniform, the net force on the dipole is zero. Due to the separation of the charges, the forces operate at various places, causing a torque on the dipole. The torque (couple) is independent of the origin when the net force is zero. Its amplitude is equal to the sum of the magnitudes of the two antiparallel forces multiplied by the couple’s arm (perpendicular distance between the two antiparallel forces). The magnitude of torque can be expressed as,
τ = q E × 2 a sinθ
τ = 2 q an E sinθ
Its direction is perpendicular to the plane of the paper, coming out of it. The magnitude of p × E is also pE sinθ and its direction is normal to the paper, coming out of it.
τ = = p × E
The dipole will tend to align with field E as a result of this torque. The torque is 0 when p is aligned with E.
If the field is not uniform, the net force will undoubtedly be greater than zero. Additionally, like before, there will be torque on the system. Because the general case is complicated, consider the simpler cases when p is parallel to E or antiparallel to E. The net torque is zero in both cases, but there is a net force on the dipole if E is not uniform.
For more detail click, Torque on an Electric Dipole in Uniform Electric Field
Physical Significance of Dipoles
With the help of electric dipole moment, we can easily determine the geometry and orientation of any compound in 3-D space.
Everything around us is made up of molecules and molecules can easily be categorized into two categories.
- Polar Molecules
- Non-Polar Molecules
Polar Molecules: The molecules which have a net dipole movement are called polar molecules. e.g. HCl. NaOH, etc. In an external electric field polar molecules align themselves in the direction of the electric field.
Non-Polar Molecules: The molecules in which individual dipole moments cancel out each other are called Non-polar molecules. i.e. in a Non-Polar molecule, the net dipole moment is Zero. e.g. CO2, O2,, etc.
Read More
Solved Examples on Electric Dipole
Example 1: Given a uniform electric field, find the flux of this field through a square of side 20 cm, whose plane is parallel to the y-z plane. What would be the flux through the same square, if the plane makes an angle of 30° with the x-axis?
Solution:
Given,
Electric field is 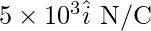
A = 10 × 10 × 10-4m2,
Flux (ϕ) = EA cos θ
Case 1,
θ = 0°,
or cos 0° = 1
Therefore, Flux, ϕ= (5 × 103) × (10 × 10 × 10-4) cos 0°
ϕ = 50 Nm2C-1
Case 2,
Angle of square plane with x-axis = 30°
Hence, the angle will be (90° – 30°) = 60°
ϕ = EA cos θ
ϕ = (5 × 103) × (10 × 10 × 10-4) × cos 60°
ϕ = 50 × 1/2
ϕ = 25 Nm2C-1
Example 2: Define the term ‘electric flux’. Write its S.I. units. What is the flux due to the electric field through a square of side 10 cm, when it is held normally too if?
Solution:
The total number of lines of force moving through an area in an electric field is known as electric flux. It’s represented by the symbol ϕ. It’s a number with a scalar value. Its S.I unit is Nm2 C-1 or Vm.
It is expressed as,
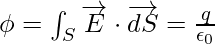
Given,
Electric field is 3×103 N/C.
Area is (10/100)×(10/100) m2 = 10-2 m2
θ = 0°,
or
cos 0° = 1
The expression for the flux can be written as,
ϕ = EA cos θ
Therefore, Flux, ϕ= (3 × 103) × (10-2) cos 0°
ϕ = 30 Nm2C-1
Electic Dipole – FAQs
What is the force acting on a dipole placed in a uniform electric field?
The net force acting on the electric dipole is zero, as the dipole consists of two opposite charges that apply force in opposite directions.
What is the SI unit of the dipole moment?
The dipole moment is measured in Coulomb-metre. It is also the SI of dipole movement.
Give an example of the electric dipole.
An example of an electric dipole is pair of electric charges of opposite signs and equal magnitude separated by a small distance.
What is the Direction of an Electric Dipole Moment?
As we know that electric dipole moment is a vector quantity so it has both magnitude and direction and its direction is always considered from the negative charge to the positive charge.
When is the torque maximum on a dipole?
If the dipole is kept perpendicular to the electric field, then the torque generated is maximum.
When is the torque minimum on a dipole?
If the dipole is kept parallel to the electric field, then the torque generated is minimum.
Why do the electric field lines not form closed loops?
Because the direction of an electric field is from positive to negative charge, it does not form closed loops. As a result, a line of force can be seen as starting with a positive charge and terminating with a negative charge.
Share your thoughts in the comments
Please Login to comment...