Electric Current in Conductors
Last Updated :
23 Apr, 2024
Charges are present in every living and non-living being on earth. In earlier centuries, charges were considered to be rest. But in the 19th century, a new phenomenon was observed about moving charges. It was observed that moving charges constitute a current. These currents occur in many situations in nature, for example – a lightning strike is a current that flows from clouds up to the ground. In everyday life, people encounter current in many electric devices.
Electric Current
Electric current is defined as the rate at which electric charge flows past a given point in a circuit. It’s measured in amperes (A), where 1 ampere is equivalent to 1 coulomb of charge flowing per second.
Ohm’s Law:
Ohm’s Law describes the relationship between current, voltage, and resistance in a circuit. It states that the current (I) flowing through a conductor is directly proportional to the voltage (V) applied across it and inversely proportional to the resistance (R) of the conductor, expressed by the equation
I = V/R
In a given time interval “t”, the charge passing through the surface can be divided into two parts – positive charges and negative charges. Let’s say q+ is the net positive charge passing through the surface in the given time interval, similarly q– is the net negative charge passing through the surface in the given time interval. In this case, the net charge passing through this surface in this interval will be,
qnet = q+ – q–
Electric current in defined as the rate of flow of charge in a conductor.
Here, I represents the average current flowing through the surface.
The unit for current is Ampere (A), Ampere stands for Column/sec.
In case when the rate of flow of charge is varying, the current flowing is given by,
I = dQ/dt
Where:
- I represents the current (measured in amperes, A)
- dQ/dt represents the rate of change of charge with respect to time (measured in coulombs per second, C/s or A)
What is Conductors?
Conductors are materials that allow electric current to flow through them easily. In these materials, electric charge carriers, typically electrons, are free to move. Metals like copper, silver, gold, and aluminum are excellent conductors of electricity due to their atomic structure.
In conductors, electrons are loosely bound to their atoms, allowing them to move relatively freely in response to an electric field. When a voltage is applied across a conductor, an electric current is established as electrons drift from areas of higher potential (positive) to areas of lower potential (negative).
Types of Conductors
These are some of the main types of conductors, each with its own unique properties and applications.
- Metallic Conductors: These are the most common type of conductors and include metals like copper, aluminum, silver, and gold.
- Superconductors: Superconductors are materials that can conduct electricity with zero resistance when cooled below a critical temperature.
- Semiconductors: While semiconductors like silicon and germanium are not as good conductors as metals, they can still carry electric current.
Electric Currents in Conductors
An electric charge experiences force if an electric field is applied, due to the force it starts moving and the movement of these charges constitutes the electric current. In a solid conductor, atoms are tightly bound with each other and approximately all the electrons are bound to the atoms. There are some electrons that are free from all the atoms are able to move freely throughout the material. When no electric field is applied, these electrons perform motion in random directions. At a given time, there is no preferential direction for the velocities of the electrons. This means, on average the number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction. So, there will be no net electric current.

Let’s see how these electrons behave when an electric field is applied to the conductor. Imagine a conductor given in the figure above, suppose one is a positively charges cylindrical disc and a negatively charged cylindrical disc. These discs are kept at the ends of a cylindrical conductor. An electric field will be created inside the conductor, this field will exert the force of charges and they will move. The movement of charges causes the electric current
Sample Problems
Question 1: Assume a horizontal plate and positive charge of 50C flows in 5 seconds through that plate. Find the magnitude of the electric current passing through that plate.
Answer:
It is known that electric current is the rate of charge passing through the conductor.
Net charge passing through the conductor qnet = 50C
Time taken, t = 5
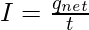
⇒ 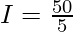
⇒ I = 10 A
Question 2: Assume a horizontal plate and positive charge of 20C flows in 2.5 seconds through that plate. Find the magnitude of the electric current passing through that plate.
Answer:
It is known that electric current is the rate of charge passing through the conductor.
Net charge passing through the conductor qnet = 20C
Time taken, t = 2.5
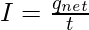
⇒ 
⇒ I = 8 A
Question 3: The charge present inside the conductor at a given time is given by the function q(t) below.
q(t) = sin(t)
Find the current flowing through the conductor at time t.
Answer:
In this case, the rate of charge through the conductor is changing. So, average current cannot be calculated, for such case instantaneous current is calculated.
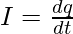
⇒ 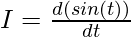
⇒ I = cos(t) A
Question 4: The charge present inside the conductor at a given time is given by the function q(t) below.
q(t) = t2 + 2t
Find the current flowing through the conductor at time t = 2.
Answer:
In this case, the rate of charge through the conductor is changing. So, average current cannot be calculated, for such case instantaneous current is calculated.
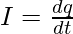
⇒ 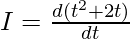
⇒ 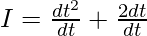
⇒ I = 2t + 2
at t = 2.
I = 2(2) + 2
⇒ I = 4 + 2
⇒ I = 6 A
Question 5: The charge present inside the conductor at a given time is given by the function q(t) below.
q(t) = t + 2t3 + et
Find the current flowing through the conductor at time t = 1.
Answer:
In this case, the rate of charge through the conductor is changing. So, average current cannot be calculated, for such case instantaneous current is calculated.
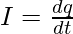
⇒ 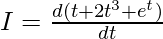
⇒ )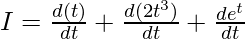
⇒ I = 1 + 6t2 + et
at t = 1.
I = 1 + 6t2 + et
⇒ I = 1 + 6(1) + e
⇒ I = 7 + e
⇒ I = 9.7A
FAQs
What factors affect the flow of current in a conductor?
The flow of current in a conductor depends on its resistance, voltage applied, and the material of the conductor. Higher resistance reduces current flow, while higher voltage increases it.
What is resistivity?
Resistivity is a property of materials that determines how strongly they oppose the flow of electric current. It’s measured in ohm-meters (Ω⋅m).
What is meant by the term ‘electric circuit’?
An electric circuit is a closed loop through which electric current can flow. It typically consists of a power source (such as a battery or generator), conductors, and loads (such as resistors or appliances).
Share your thoughts in the comments
Please Login to comment...