Diffraction is a phenomenon shown by light. When the wave of light interacts with the particle in the atmosphere it bends at the corners and scatters in the area to illuminate the whole area, this phenomenon is called the Diffraction of light. It is a property of light which is used to explain various phenomena observed in our daily life.
Let’s learn about diffraction in detail in this article.
What is Diffraction?
Bending of light around corners such that it spreads out and illuminates’ regions is known as diffraction.
Diffraction can be observed easily when we replace the double slit of the young double slit experiment with a single narrow slit. As the light passes this narrow slit a bright pattern at the centre is observed.
The diffraction phenomenon is very similar to the interference phenomenon and they both happen simultaneously. Generally, it’s difficult to distinguish between diffraction and interference since they both happen at the same time. Diffraction is observed when light is diffracted from water droplets in the clouds and we see shades of blue, pink, purple, and green in clouds.
Check: Difference Between Diffraction and Interference
Diffraction Examples
Examples of diffraction can easily be observed in our daily life, some of the most common ones are, the silver lining seen on the edges of the clouds because of the diffraction of light by water droplets.
The intensity of the diffraction of light varies with the wavelength of the light used where the light with a higher wavelength diffracts in comparison to light with a smaller wavelength.
Types of Diffraction
We can categorise diffraction into two categories that are,
- Fraunhofer Diffraction
- Fresnel Diffraction
Fraunhofer Diffraction
- When all the light rays passing through the narrow slit are parallel to each other then the diffraction which occurs is called Fraunhofer Diffraction.
- This diffraction is achieved by placing the light source far away from the narrow slit.
- The screen and the source are at an infinite distance from each other in this type of diffraction. Fraunhofer Diffraction uses a convex lens to produce a diffracting pattern.
Fresnel Diffraction
- If the light source and screen at which the diffraction pattern is obtained are at finite distances then the diffraction is called Fresnel Diffraction.
- In Fresnel Diffraction, the shapes obtained from the incident wavefronts are spherical. In this type of diffraction, a convex lens is not required.
Check: Applications of Diffraction of Light
Single Slit Diffraction
We may see the bending phenomena of light, or diffraction, in the single-slit diffraction experiment, which causes light from a coherent source to interfere with itself and form a distinct pattern on the screen termed the diffraction pattern. When the sources are tiny enough to be comparable in size to the wavelength of light, diffraction occurs. This impact may be seen in the diagram below,
.png)
Denote the slit width as ‘a’, and the distance between the slit and the screen as D such that a<<<D.
.png)
The angular location of any point on the screen will be determined by measuring from the slit centre, which splits the slit by a ⁄ 2 lengths. To explain the pattern, we’ll look at the state of black fringes first. Let us also split the slit into equal-width zones a ⁄ 2. Let’s take a look at a pair of rays that come from a ⁄ 2 distances apart, as illustrated below.
.png)
The top two rays indicate the following route difference:
Δ L = (a ⁄ 2) sinθ
Note: Remember that this is only a viable computation if D is really large.
Any number of ray pairs that start at a distance of a ⁄ 2 from one another, such as the bottom two rays in the diagram, can be considered. Any arbitrary pair of rays separated by a ⁄ 2 can be taken into account. In a minute, we’ll discover how important this method is.
The path difference must create destructive interference for a dark fringe; the path difference must be out of phase by λ ⁄ 2. (λ represents the wavelength)
For the first fringe,
Δ L = λ ⁄ 2 = a ⁄ 2 sinθ
λ = a sinθ
There is another beam at a distance of a ⁄ 2 that can create destructive interference for a ray coming from any point in the slit. As each ray originating from a point has a counterpart that produces destructive interference, there is destructive interference at θ = sin−1(λ ⁄ a). As a result, a dark fringe is created.
We may divide the slit into four equal portions of a ⁄ 4 and use the same rationale for the next fringe. As a result, for the second minima,
λ ⁄ 2 = a ⁄ 4 sinθ
2λ = a sinθ
Similarly, we may divide the slit into 2n parts for the nth fringe and utilise the following condition:
λ ⁄ 2 = a ⁄ 2n sinθ
n λ = a sinθ
Central Maximum
The maxima are located between the minima, and the width of the central maximum is equal to the distance between the 1st order minima on both sides of the screen.
The position of the minima determined by y (as measured from the screen’s centre) is,
tanθ ≈ θ ≈ y ⁄ D
For small θ,
sinθ ≈ θ
λ = a sinθ ≈ a θ
Angular width,
θ = y/D = λa
Central maximum,
y = λ D a
The centre maximum’s width is just twice this amount.
Width of central maximum = 2λ D a
Angular width of central maximum = 2θ = 2λ a
Check: Problems on Diffraction – Class 12 Physics
Resolving Power
- The resolving power of an optical instrument is defined as the capacity of the instrument to distinguish between two objects that are close together and produce distinct images of the two objects.
- In other words, resolving power changes in inverse proportion to the distance between the two objects to be resolved when viewed from an optical instrument. The images of two close-lying objects appear distinct and separate when viewed from the device.
- When a telescope is used to view two stars located close to each other; the telescope’s resolving power will depend on its capacity to resolve the images of the two stars.
- The resolving power of a lens used in a telescope can be determined by its ability to differentiate two lines or points in an object.
Check: Diffraction Grating Formula
Rayleigh’s Criterion
The minimum distances between images must be such that the central maximum of the first image lies on the first minimum of the second and vice versa. Such an image viewed from an optical device is calculated using Rayleigh’s criterion.
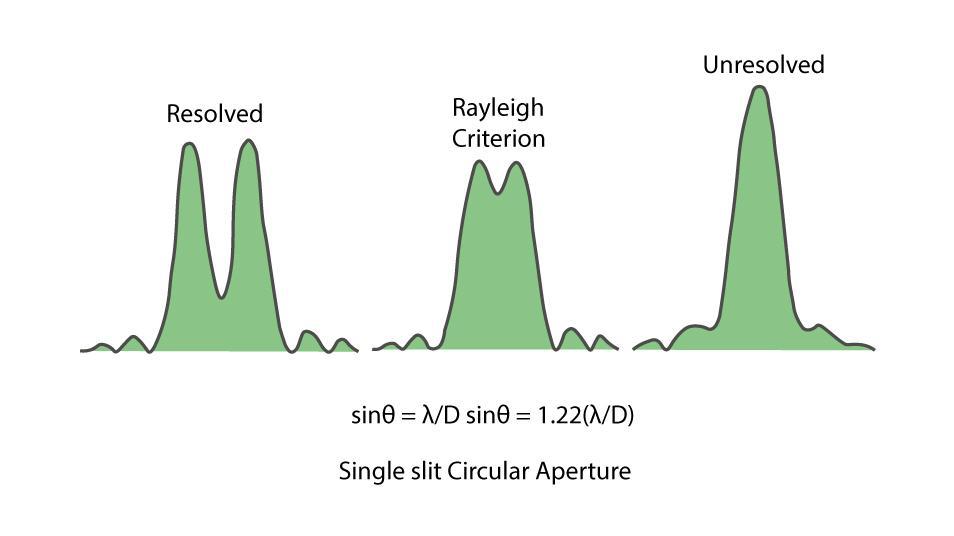
When two objects placed at a distance from each other are separated by an angular separation θ, the diffraction patterns of the two objects will overlap each other. They would appear as one when the two central maxima overlap.
This defines Rayleigh’s resolution criterion. It can be shown that, for a circular aperture of a given diameter, the first minimum in the diffraction pattern occurs at,
θ = 1.22(λ/D)
where,
θ is the angular separation measured in radians
λ is the wavelength of light
D is the diameter of the aperture
Check: Resolving Power of a Microscope and Telescope
What Is the Difference Between Diffraction and Scattering?
The terms diffraction and scattering are often used interchangeably and are considered to be almost synonymous. Diffraction describes a specialized case of light scattering in which an object with regularly repeating features (such as a diffraction grating) produces an orderly diffraction of light in a diffraction pattern. In the real world, most objects are very complex in shape and should be considered to be composed of many individual diffraction features that can collectively produce a random scattering of light.
Read More:
Conclusion of Diffraction of Light
Light diffraction shows how light waves bend and spread when they come into contact with objects or squeeze through narrow spaces. This phenomena is important for many optical applications, such as developing sophisticated optical systems like diffraction gratings or producing rainbows. Knowing diffraction allows for the creation of cutting-edge spectroscopy, microscopy, and telecommunications technologies.
Diffraction of Light – FAQs
What is meant by the diffraction of light?
The phenomenon of bending of light around the edge of the particle is called the diffraction of light.
What is the essential condition for the diffraction of light to occur?
The essential condition for the diffraction of light to occur is the length of the obstacle must be comparable to the wavelength of light.
What is the Phase Difference?
The difference in the phase angle of the two waves is called the phase difference whereas the difference in the path covered by the two waves is called the path difference.,
What is the Condition for Constructive Interference?
If the phase difference between two certain waves is an even multiple of π then constructive interference occurs, also path difference must be an integral multiple of the wavelength.
What is the condition for destructive interference?
If the phase difference between two certain waves is an odd multiple of π then destructive interference occurs.
What is Total Internal Reflection?
When a light ray goes from a denser medium to a rarer medium at an angle greater than the critical angle it gets reflected instead of being refracted this phenomenon is called Total Internal Reflection.
What is the Formula for the Width of the Central Maxima?
The Formula for the Width of the Central Maxima is,
θ = 2λa
Share your thoughts in the comments
Please Login to comment...