Analysis of Algorithms | Big-Omega Ω Notation
Last Updated :
29 Mar, 2024
In the analysis of algorithms, asymptotic notations are used to evaluate the performance of an algorithm, in its best cases and worst cases. This article will discuss Big-Omega Notation represented by a Greek letter (Ω).
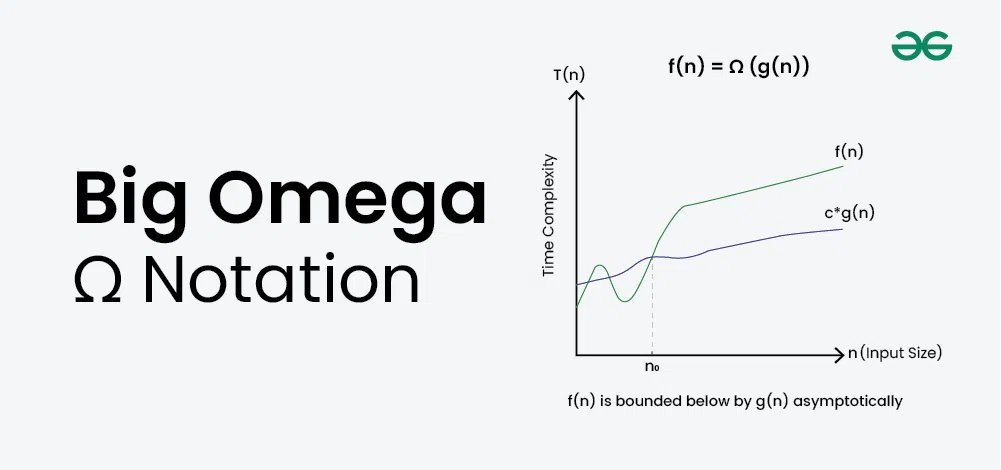
What is Big-Omega Ω Notation?
Big-Omega Ω Notation, is a way to express the asymptotic lower bound of an algorithm’s time complexity, since it analyses the best-case situation of algorithm. It provides a lower limit on the time taken by an algorithm in terms of the size of the input. It’s denoted as Ω(f(n)), where f(n) is a function that represents the number of operations (steps) that an algorithm performs to solve a problem of size n.
Big-Omega Ω Notation is used when we need to find the asymptotic lower bound of a function. In other words, we use Big-Omega Ω when we want to represent that the algorithm will take at least a certain amount of time or space.
Definition of Big-Omega Ω Notation?
Given two functions g(n) and f(n), we say that f(n) = Ω(g(n)), if there exists constants c > 0 and n0 >= 0 such that f(n) >= c*g(n) for all n >= n0.
In simpler terms, f(n) is Ω(g(n)) if f(n) will always grow faster than c*g(n) for all n >= n0 where c and n0 are constants.
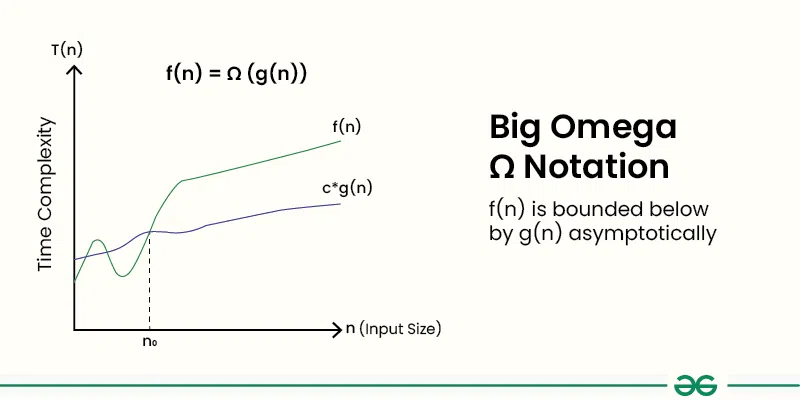
How to Determine Big-Omega Ω Notation?
In simple language, Big-Omega Ω notation specifies the asymptotic lower bound for a function f(n). It bounds the growth of the function from below as the input grows infinitely large.
Steps to Determine Big-Omega Ω Notation:
1. Break the program into smaller segments:
- Break the algorithm into smaller segments such that each segment has a certain runtime complexity.
2. Find the complexity of each segment:
- Find the number of operations performed for each segment(in terms of the input size) assuming the given input is such that the program takes the least amount of time.
3. Add the complexity of all segments:
- Add up all the operations and simplify it, let’s say it is f(n).
4. Remove all the constants:
- Remove all the constants and choose the term having the least order or any other function which is always less than f(n) when n tends to infinity.
- Let’s say the least order function is g(n) then, Big-Omega (Ω) of f(n) is Ω(g(n)).
Example of Big-Omega Ω Notation:
Consider an example to print all the possible pairs of an array. The idea is to run two nested loops to generate all the possible pairs of the given array:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to print all possible pairs
int print(int a[], int n)
{
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i != j)
cout << a[i] << " " << a[j] << "\n";
}
}
}
// Driver Code
int main()
{
// Given array
int a[] = { 1, 2, 3 };
// Store the size of the array
int n = sizeof(a) / sizeof(a[0]);
// Function Call
print(a, n);
return 0;
}
// Java program for the above approach
import java.lang.*;
import java.util.*;
class GFG{
// Function to print all possible pairs
static void print(int a[], int n)
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
if (i != j)
System.out.println(a[i] + " " + a[j]);
}
}
}
// Driver code
public static void main(String[] args)
{
// Given array
int a[] = { 1, 2, 3 };
// Store the size of the array
int n = a.length;
// Function Call
print(a, n);
}
}
// This code is contributed by avijitmondal1998
// C# program for above approach
using System;
class GFG{
// Function to print all possible pairs
static void print(int[] a, int n)
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
if (i != j)
Console.WriteLine(a[i] + " " + a[j]);
}
}
}
// Driver Code
static void Main()
{
// Given array
int[] a = { 1, 2, 3 };
// Store the size of the array
int n = a.Length;
// Function Call
print(a, n);
}
}
// This code is contributed by sanjoy_62.
<script>
// JavaScript program for the above approach
// Function to print all possible pairs
function print(a, n)
{
for(let i = 0; i < n; i++)
{
for(let j = 0; j < n; j++)
{
if (i != j)
document.write(a[i] + " " +
a[j] + "<br>");
}
}
}
// Driver Code
// Given array
let a = [ 1, 2, 3 ];
// Store the size of the array
let n = a.length;
// Function Call
print(a, n);
// This code is contributed by code_hunt
</script>
# Python3 program for the above approach
# Function to print all possible pairs
def printt(a, n) :
for i in range(n) :
for j in range(n) :
if (i != j) :
print(a[i], "", a[j])
# Driver Code
# Given array
a = [ 1, 2, 3 ]
# Store the size of the array
n = len(a)
# Function Call
printt(a, n)
# This code is contributed by splevel62.
Output1 2
1 3
2 1
2 3
3 1
3 2
In this example, it is evident that the print statement gets executed n2 times. Now linear functions g(n), logarithmic functions g(log n), constant functions g(1) will always grow at a lesser rate than n2 when the input range tends to infinity therefore, the best-case running time of this program can be Ω(log n), Ω(n), Ω(1), or any function g(n) which is less than n2 when n tends to infinity.
When to use Big-Omega Ω notation?
Big-Omega Ω notation is the least used notation for the analysis of algorithms because it can make a correct but imprecise statement over the performance of an algorithm.
Suppose a person takes 100 minutes to complete a task, then using Ω notation it can be stated that the person takes more than 10 minutes to do the task, this statement is correct but not precise as it doesn’t mention the upper bound of the time taken. Similarly, using Ω notation we can say that the best-case running time for the binary search is Ω(1), which is true because we know that binary search would at least take constant time to execute but not very precise as in most of the cases binary search takes log(n) operations to complete.
Difference between Big-Omega Ω and Little-Omega ω notation:
Parameters
| Big-Omega Ω Notation
| Little-Omega ω Notation
|
|---|
Description
| Big-Omega (Ω) describes the tight lower bound notation.
| Little-Omega(ω) describes the loose lower bound notation.
|
|---|
Formal Definition
| Given two functions g(n) and f(n), we say that f(n) = Ω(g(n)), if there exists constants c > 0 and n0 >= 0 such that f(n) >= c*g(n) for all n >= n0.
| Given two functions g(n) and f(n), we say that f(n) = ω(g(n)), if there exists constants c > 0 and n0 >= 0 such that f(n) > c*g(n) for all n >= n0.
|
|---|
Representation
| f(n) = ω(g(n)) represents that f(n) grows strictly faster than g(n) asymptotically.
| f(n) = Ω(g(n)) represents that f(n) grows at least as fast as g(n) asymptotically.
|
|---|
Frequently Asked Questions about Big-Omega Ω notation:
Question 1: What is Big-Omega Ω notation?
Answer: Big-Omega Ω notation, is a way to express the asymptotic lower bound of an algorithm’s time complexity, since it analyses the best-case situation of algorithm. It provides a lower limit on the time taken by an algorithm in terms of the size of the input.
Question 2: What is the equation of Big-Omega (Ω)?
Answer: The equation for Big-Omega Ω is:
Given two functions g(n) and f(n), we say that f(n) = Ω(g(n)), if there exists constants c > 0 and n0 >= 0 such that f(n) >= c*g(n) for all n >= n0.
Question 3: What does the notation Omega mean?
Answer: Big-Omega Ω means the asymptotic lower bound of a function. In other words, we use Big-Ω represents the least amount of time or space the algorithm takes to run.
Question 4: What is the difference between Big-Omega Ω and Little-Omega ω notation?
Answer: Big-Omega (Ω) describes the tight lower bound notation whereas Little-Omega(ω) describes the loose lower bound notation.
Question 5: Why is Big-Omega Ω used?
Answer: Big-Omega Ω is used to specify the best-case time complexity or the lower bound of a function. It is used when we want to know the least amount of time that a function will take to execute.
Question 6: How is Big Omega Ω notation different from Big O notation?
Answer: Big Omega notation (Ω(f(n))) represents the lower bound of an algorithm’s complexity, indicating that the algorithm will not perform better than this lower bound, Whereas Big O notation (O(f(n))) represents the upper bound or worst-case complexity of an algorithm.
Question 7: What does it mean if an algorithm has a Big Omega complexity of Ω(n)?
Answer: If an algorithm has a Big Omega complexity of Ω(n), it means that the algorithm’s performance is at least linear in relation to the input size. In other words, the algorithm’s running time or space usage grows at least proportionally to the input size.
Question 8: Can an algorithm have multiple Big Omega Ω complexities?
Answer: Yes, an algorithm can have multiple Big Omega complexities depending on different input scenarios or conditions within the algorithm. Each complexity represents a lower bound for specific cases.
Question 9: How does Big Omega complexity relate to best-case performance analysis?
Answer: Big Omega complexity is closely related to best-case performance analysis because it represents the lower bound of an algorithm’s performance. However, it’s important to note that the best-case scenario may not always coincide with the Big Omega complexity.
Question 10: In what scenarios is understanding Big Omega complexity particularly important?
Answer: Understanding Big Omega complexity is important when we need to guarantee a certain level of performance or when we want to compare the efficiencies of different algorithms in terms of their lower bounds.
Related Articles:
Share your thoughts in the comments
Please Login to comment...