Diagonal Sum of a Binary Tree

Difficulty Level : Medium
Last Updated : 24 Sep, 2021

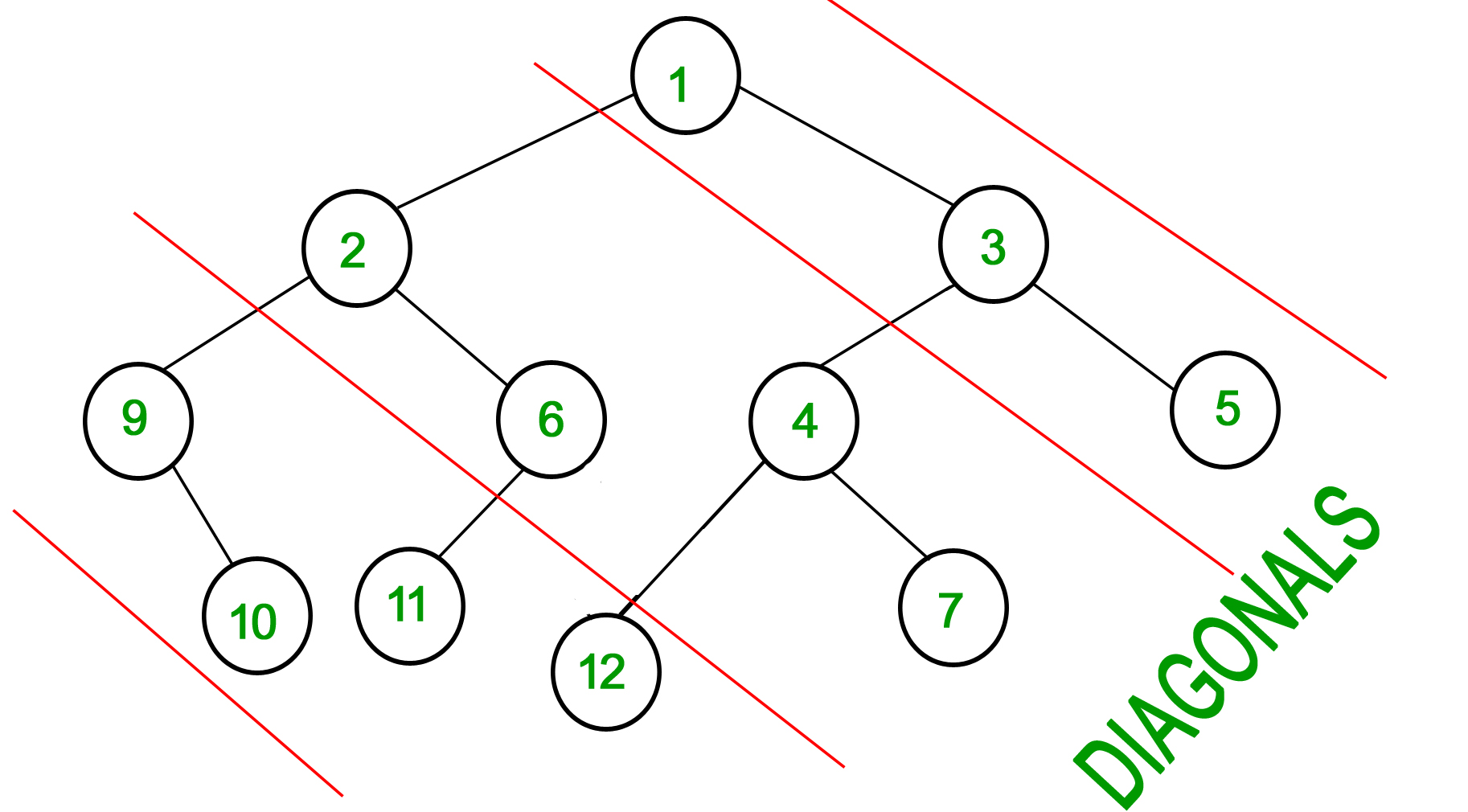
Consider lines of slope -1 passing between nodes (dotted lines in below diagram). The diagonal sum in a binary tree is the sum of all node’s data lying between these lines. Given a Binary Tree, print all diagonal sums.
For the following input tree, the output should be 9, 19, 42.
9 is sum of 1, 3 and 5.
19 is sum of 2, 6, 4 and 7.
42 is sum of 9, 10, 11 and 12.

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.

Method 1

Algorithm:
The idea is to keep track of vertical distance from top diagonal passing through the root. We increment the vertical distance we go down to next diagonal.

Add root with vertical distance as 0 to the queue.
Process the sum of all right child and right of the right child and so on.
Add left child current node into the queue for later processing. The vertical distance of the left child is the vertical distance of current node plus 1.
Keep doing 2nd, 3rd and 4th step till the queue is empty.

Following is the implementation of the above idea.

C++

// C++ Program to find diagonal
// sum in a Binary Tree
#include <bits/stdc++.h>
using namespace std;
 
struct Node
{
    int data;
    struct Node* left;
    struct Node* right;
};
 
struct Node* newNode(int data)
{
    struct Node* Node =
            (struct Node*)malloc(sizeof(struct Node));
     
    Node->data = data;
    Node->left = Node->right = NULL;
 
    return Node;
}
 
// root - root of the binary tree
// vd - vertical distance diagonally
// diagonalSum - map to store Diagonal
// Sum(Passed by Reference)
void diagonalSumUtil(struct Node* root,
                int vd, map<int, int> &diagonalSum)
{
    if(!root)
        return;
         
    diagonalSum[vd] += root->data;
 
    // increase the vertical distance if left child
    diagonalSumUtil(root->left, vd + 1, diagonalSum);
 
    // vertical distance remains same for right child
    diagonalSumUtil(root->right, vd, diagonalSum);
}
 
// Function to calculate diagonal
// sum of given binary tree
void diagonalSum(struct Node* root)
{
 
    // create a map to store Diagonal Sum
    map<int, int> diagonalSum;
     
    diagonalSumUtil(root, 0, diagonalSum);
 
    map<int, int>::iterator it;
        cout << "Diagonal sum in a binary tree is - ";
     
    for(it = diagonalSum.begin();
                it != diagonalSum.end(); ++it)
    {
        cout << it->second << " ";
    }
}
 
// Driver code
int main()
{
    struct Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(9);
    root->left->right = newNode(6);
    root->right->left = newNode(4);
    root->right->right = newNode(5);
    root->right->left->right = newNode(7);
    root->right->left->left = newNode(12);
    root->left->right->left = newNode(11);
    root->left->left->right = newNode(10);
 
    diagonalSum(root);
 
    return 0;
}
 
// This code is contributed by Aditya Goel

Java

// Java Program to find diagonal sum in a Binary Tree
import java.util.*;
import java.util.Map.Entry;
 
//Tree node
class TreeNode
{
    int data; //node data
    int vd; //vertical distance diagonally
    TreeNode left, right; //left and right child's reference
 
    // Tree node constructor
    public TreeNode(int data)
    {
        this.data = data;
        vd = Integer.MAX_VALUE;
        left = right = null;
    }
}
 
// Tree class
class Tree
{
    TreeNode root;//Tree root
 
    // Tree constructor
    public Tree(TreeNode root)  {  this.root = root;  }
 
    // Diagonal sum method
    public void diagonalSum()
    {
        // Queue which stores tree nodes
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
 
        // Map to store sum of node's data lying diagonally
        Map<Integer, Integer> map = new TreeMap<>();
 
        // Assign the root's vertical distance as 0.
        root.vd = 0;
 
        // Add root node to the queue
        queue.add(root);
 
        // Loop while the queue is not empty
        while (!queue.isEmpty())
        {
            // Remove the front tree node from queue.
            TreeNode curr = queue.remove();
 
            // Get the vertical distance of the dequeued node.
            int vd = curr.vd;
 
            // Sum over this node's right-child, right-of-right-child
            // and so on
            while (curr != null)
            {
                int prevSum = (map.get(vd) == null)? 0: map.get(vd);
                map.put(vd, prevSum + curr.data);
 
                // If for any node the left child is not null add
                // it to the queue for future processing.
                if (curr.left != null)
                {
                    curr.left.vd = vd+1;
                    queue.add(curr.left);
                }
 
                // Move to the current node's right child.
                curr = curr.right;
            }
        }
 
        // Make an entry set from map.
        Set<Entry<Integer, Integer>> set = map.entrySet();
 
        // Make an iterator
        Iterator<Entry<Integer, Integer>> iterator = set.iterator();
 
        // Traverse the map elements using the iterator.
         System.out.print("Diagonal sum in a binary tree is - ");
        while (iterator.hasNext())
        {
            Map.Entry<Integer, Integer> me = iterator.next();
 
            System.out.print(me.getValue()+" ");
        }
    }
}
 
//Driver class
public class DiagonalSum
{
    public static void main(String[] args)
    {
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(9);
        root.left.right = new TreeNode(6);
        root.right.left = new TreeNode(4);
        root.right.right = new TreeNode(5);
        root.right.left.left = new TreeNode(12);
        root.right.left.right = new TreeNode(7);
        root.left.right.left = new TreeNode(11);
        root.left.left.right = new TreeNode(10);
        Tree tree = new Tree(root);
        tree.diagonalSum();
    }
}

Python3

# Program to find diagonal sum in a Binary Tree
 
class newNode:
    def __init__(self, data):
        self.data = data
        self.left = self.right = None
         
# Function to compute height and
# root - root of the binary tree
# vd - vertical distance diagonally
# diagonalSum - map to store Diagonal
# Sum(Passed by Reference)
def diagonalSumUtil(root, vd, diagonalSum) :
 
    if(not root):
        return
         
    if vd not in diagonalSum:
        diagonalSum[vd] = 0
    diagonalSum[vd] += root.data
 
    # increase the vertical distance
    # if left child
    diagonalSumUtil(root.left, vd + 1,
                          diagonalSum)
 
    # vertical distance remains same
    # for right child
    diagonalSumUtil(root.right, vd,
                       diagonalSum)
 
# Function to calculate diagonal
# sum of given binary tree
def diagonalSum(root) :
 
    # create a map to store Diagonal Sum
    diagonalSum = dict()
     
    diagonalSumUtil(root, 0, diagonalSum)
 
    print("Diagonal sum in a binary tree is - ",
                                       end = "")
     
    for it in diagonalSum:
        print(diagonalSum[it], end = " ")
         
# Driver Code
if __name__ == '__main__':
    root = newNode(1)
    root.left = newNode(2)
    root.right = newNode(3)
    root.left.left = newNode(9)
    root.left.right = newNode(6)
    root.right.left = newNode(4)
    root.right.right = newNode(5)
    root.right.left.right = newNode(7)
    root.right.left.left = newNode(12)
    root.left.right.left = newNode(11)
    root.left.left.right = newNode(10)
 
    diagonalSum(root)
 
# This code is contributed
# by SHUBHAMSINGH10

C#

// C# Program to find diagonal sum in a Binary Tree
using System;
using System.Collections.Generic;
 
// Tree node
public
 
  class TreeNode
  {
    public
      int data; // node data
    public
 
      int vd; // vertical distance diagonally
    public
      TreeNode left, right; // left and right child's reference
 
    // Tree node constructor
    public TreeNode(int data)
    {
      this.data = data;
      vd = int.MaxValue;
      left = right = null;
    }
  }
 
// Tree class
public class Tree
{
  TreeNode root;//T ree root
 
  // Tree constructor
  public Tree(TreeNode root)
  {
    this.root = root;
  }
 
  // Diagonal sum method
  public void diagonalSum()
  {
 
    // Queue which stores tree nodes
    Queue<TreeNode> queue = new Queue<TreeNode>();
 
    // Map to store sum of node's data lying diagonally
    Dictionary<int, int> map = new Dictionary<int,int>();
 
    // Assign the root's vertical distance as 0.
    root.vd = 0;
 
    // Add root node to the queue
    queue.Enqueue(root);
 
    // Loop while the queue is not empty
    while (queue.Count != 0)
    {
 
      // Remove the front tree node from queue.
      TreeNode curr = queue.Dequeue();
 
      // Get the vertical distance of the dequeued node.
      int vd = curr.vd;
 
      // Sum over this node's right-child, right-of-right-child
      // and so on
      while (curr != null)
      {
        int prevSum;
        if(!map.ContainsKey(vd))
          prevSum = 0;
        else
          prevSum =  map[vd];
 
        if(map.ContainsKey(vd))
          map[vd] =  prevSum + curr.data;
        else
          map.Add(vd, prevSum + curr.data);
 
        // If for any node the left child is not null add
        // it to the queue for future processing.
        if (curr.left != null)
        {
          curr.left.vd = vd + 1;
          queue.Enqueue(curr.left);
        }
 
        // Move to the current node's right child.
        curr = curr.right;
      }
    }
 
 
    // Traverse the map elements using the iterator.
    Console.Write("Diagonal sum in a binary tree is - ");
    foreach(KeyValuePair<int, int> iterator in map)
    {
 
      //  Map.Entry<int, int> me = iterator.next();
      Console.Write(iterator.Value + " ");
    }
  }
}
 
// Driver class
public class DiagonalSum
{
  public static void Main(String[] args)
  {
    TreeNode root = new TreeNode(1);
    root.left = new TreeNode(2);
    root.right = new TreeNode(3);
    root.left.left = new TreeNode(9);
    root.left.right = new TreeNode(6);
    root.right.left = new TreeNode(4);
    root.right.right = new TreeNode(5);
    root.right.left.left = new TreeNode(12);
    root.right.left.right = new TreeNode(7);
    root.left.right.left = new TreeNode(11);
    root.left.left.right = new TreeNode(10);
    Tree tree = new Tree(root);
    tree.diagonalSum();
  }
}
 
// This code is contributed by gauravrajput1

Javascript

<script>
 
      // JavaScript Program to find diagonal
      // sum in a Binary Tree
      // Tree node
      class TreeNode {
        // Tree node constructor
        constructor(data) {
          this.data = data; // node data
          this.vd = 2147483647; // vertical distance diagonally
          this.left = null; // left and right child's reference
          this.right = null;
        }
      }
 
      // Tree class
      class Tree {
        // Tree constructor
        constructor(root) {
          this.root = root; //T ree root
        }
 
        // Diagonal sum method
        diagonalSum() {
          // Queue which stores tree nodes
          var queue = [];
 
          // Map to store sum of node's data lying diagonally
          var map = {};
 
          // Assign the root's vertical distance as 0.
          this.root.vd = 0;
 
          // Add root node to the queue
          queue.push(this.root);
 
          // Loop while the queue is not empty
          while (queue.length != 0) {
            // Remove the front tree node from queue.
            var curr = queue.shift();
 
            // Get the vertical distance of the dequeued node.
            var vd = curr.vd;
 
            // Sum over this node's right-child,
            // right-of-right-child
            // and so on
            while (curr != null) {
              var prevSum;
              if (!map.hasOwnProperty(vd))
              prevSum = 0;
              else prevSum = map[vd];
 
              if (map.hasOwnProperty(vd))
              map[vd] = prevSum + curr.data;
              else
              map[vd] = prevSum + curr.data;
 
              // If for any node the left child is not null add
              // it to the queue for future processing.
              if (curr.left != null) {
                curr.left.vd = vd + 1;
                queue.push(curr.left);
              }
 
              // Move to the current node's right child.
              curr = curr.right;
            }
          }
 
          // Traverse the map elements using the iterator.
          document.write("Diagonal sum in a binary tree is - ");
          for (const [key, value] of Object.entries(map)) {
            // Map.Entry<int, int> me = iterator.next();
            document.write(value + " ");
          }
        }
      }
 
      // Driver class
      var root = new TreeNode(1);
      root.left = new TreeNode(2);
      root.right = new TreeNode(3);
      root.left.left = new TreeNode(9);
      root.left.right = new TreeNode(6);
      root.right.left = new TreeNode(4);
      root.right.right = new TreeNode(5);
      root.right.left.left = new TreeNode(12);
      root.right.left.right = new TreeNode(7);
      root.left.right.left = new TreeNode(11);
      root.left.left.right = new TreeNode(10);
      var tree = new Tree(root);
      tree.diagonalSum();
       
</script>

Output

Diagonal sum in a binary tree is - 9 19 42

Exercise:
This problem was for diagonals from top to bottom and slope -1. Try the same problem for slope +1.
This article is contributed by Kumar Gautam. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

Method 2:

The idea behind this method is inspired by the diagonal relation in matrices. We can observe that all the elements lying on the same diagonal in a matrix have their difference of row and column same. For instance, consider the main diagonal in a square matrix, we can observe the difference of the respective row and column indices of each element on diagonal is same, i.e. each element on the main diagonal have the difference of row and column 0, eg: 0-0, 1-1, 2-2,…n-n.

Similarly, every diagonal has its own unique difference of rows and column, and with the help of this, we can identify each element, that to which diagonal it belongs.

The same idea is applied to solve this problem-

We will treat the level of the tree nodes as their row indices, and width of the tree nodes as their column indices.
We will denote the cell of each node as (level, width)

Example- (Taking the same tree as above)

Nodes	Level Index	Width Index
1	0	0
2	1	-1
3	1	1
4	2	0
5	2	2
6	2	0
7	3	1
9	2	-2
10	3	-1
11	3	-1
12	3	-1

To help you visualize let’s draw a matrix, the first row and first column, are respective width and level indices-

	-2	-1	0	1	2
0			1
1		2		3
2	9		6+4		5
3		10+11+12		7

Below is the implementation of the above idea:

C++

// C++ Program to calculate the
// sum of diagonal nodes.
 
#include <bits/stdc++.h>
using namespace std;
 
// Node Structure
struct Node {
    int data;
    Node *left, *right;
};
 
// to map the node with level - index
map<int, int> grid;
 
// Function to create new node
struct Node* newNode(int data)
{
    struct Node* Node
        = (struct Node*)malloc(sizeof(struct Node));
 
    Node->data = data;
    Node->left = Node->right = NULL;
 
    return Node;
}
 
// recursvise function to calculate sum of elements
// where level - index is same.
void addConsideringGrid(Node* root, int level, int index)
{
 
    // if there is no child then return
    if (root == NULL)
        return;
 
    // add the element in the group of node
    // whose level - index is equal
    grid[level - index] += (root->data);
 
    // left child call
    addConsideringGrid(root->left, level + 1, index - 1);
 
    // right child call
    addConsideringGrid(root->right, level + 1, index + 1);
}
 
vector<int> diagonalSum(Node* root)
{
    grid.clear();
 
    // Function call
    addConsideringGrid(root, 0, 0);
    vector<int> ans;
 
    // for different values of level - index
    // add te sum of those node to answer
    for (auto x : grid) {
        ans.push_back(x.second);
    }
 
    return ans;
}
 
// Driver code
int main()
{
 
    // build binary tree
    struct Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(9);
    root->left->right = newNode(6);
    root->right->left = newNode(4);
    root->right->right = newNode(5);
    root->right->left->right = newNode(7);
    root->right->left->left = newNode(12);
    root->left->right->left = newNode(11);
    root->left->left->right = newNode(10);
 
    // Function Call
    vector<int> v = diagonalSum(root);
 
    // print the diagonal sums
    for (int i = 0; i < v.size(); i++)
        cout << v[i] << " ";
      return 0;
}

Java

// Java Program to calculate the
// sum of diagonal nodes.
import java.util.*;
class GFG
{
 
// Node Structure
static class Node
{
    int data;
    Node left, right;
};
 
// to map the node with level - index
static HashMap<Integer,Integer> grid = new HashMap<>();
 
// Function to create new node
static Node newNode(int data)
{
    Node Node = new Node();
    Node.data = data;
    Node.left = Node.right = null;
    return Node;
}
 
// recursvise function to calculate sum of elements
// where level - index is same.
static void addConsideringGrid(Node root, int level, int index)
{
 
    // if there is no child then return
    if (root == null)
        return;
 
    // add the element in the group of node
    // whose level - index is equal
    if(grid.containsKey(level-index))
    grid.put(level - index,grid.get(level-index) + (root.data));
    else
        grid.put(level-index, root.data);
 
    // left child call
    addConsideringGrid(root.left, level + 1, index - 1);
 
    // right child call
    addConsideringGrid(root.right, level + 1, index + 1);
}
 
static Vector<Integer> diagonalSum(Node root)
{
    grid.clear();
 
    // Function call
    addConsideringGrid(root, 0, 0);
    Vector<Integer> ans = new Vector<>();
 
    // for different values of level - index
    // add te sum of those node to answer
    for (Map.Entry<Integer,Integer> x : grid.entrySet())
    {
        ans.add(x.getValue());
    }
    return ans;
}
 
// Driver code
public static void main(String[] args)
{
 
    // build binary tree
    Node root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(9);
    root.left.right = newNode(6);
    root.right.left = newNode(4);
    root.right.right = newNode(5);
    root.right.left.right = newNode(7);
    root.right.left.left = newNode(12);
    root.left.right.left = newNode(11);
    root.left.left.right = newNode(10);
 
    // Function Call
    Vector<Integer> v = diagonalSum(root);
 
    // print the diagonal sums
    for (int i = 0; i < v.size(); i++)
        System.out.print(v.get(i) + " ");
  }
}
 
// This code is contributed by Rajput-Ji .

Python3

# Python3 program calculate the
# sum of diagonal nodes.
from collections import deque
 
# A binary tree node structure
class Node:
    def __init__(self, key):
         
        self.data = key
        self.left = None
        self.right = None
 
# To map the node with level - index
grid = {}
 
# Recursvise function to calculate
# sum of elements where level - index
# is same
def addConsideringGrid(root, level, index):
     
    global grid
 
    # If there is no child then return
    if (root == None):
        return
 
    # Add the element in the group of node
    # whose level - index is equal
    grid[level - index] = (grid.get(level - index, 0) +
                           root.data)
 
    # Left child call
    addConsideringGrid(root.left, level + 1,
                                  index - 1)
 
    # Right child call
    addConsideringGrid(root.right, level + 1,
                                   index + 1)
 
def diagonalSum(root):
     
    # grid.clear()
 
    # Function call
    addConsideringGrid(root, 0, 0)
    ans = []
 
    # For different values of level - index
    # add te sum of those node to answer
    for x in grid:
        ans.append(grid[x])
 
    return ans
 
# Driver code
if __name__ == '__main__':
     
    # Build binary tree
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(9)
    root.left.right = Node(6)
    root.right.left = Node(4)
    root.right.right = Node(5)
    root.right.left.right = Node(7)
    root.right.left.left = Node(12)
    root.left.right.left = Node(11)
    root.left.left.right = Node(10)
 
    # Function Call
    v = diagonalSum(root)
 
    # Print the diagonal sums
    for i in v:
        print(i, end = " ")
 
# This code is contributed by mohit kumar 29

C#

// C# Program to calculate the
// sum of diagonal nodes.
using System;
using System.Collections.Generic;
public class GFG
{
 
// Node Structure
public
 class Node
{
    public
 int data;
    public
 Node left, right;
};
 
// to map the node with level - index
static Dictionary<int, int> grid = new Dictionary<int, int>();
 
// Function to create new node
static Node newNode(int data)
{
    Node Node = new Node();
    Node.data = data;
    Node.left = Node.right = null;
    return Node;
}
 
// recursvise function to calculate sum of elements
// where level - index is same.
static void addConsideringGrid(Node root, int level, int index)
{
 
    // if there is no child then return
    if (root == null)
        return;
 
    // add the element in the group of node
    // whose level - index is equal
    if(grid.ContainsKey(level - index))
    grid[level - index] = grid[level - index] + (root.data);
    else
        grid.Add(level-index, root.data);
 
    // left child call
    addConsideringGrid(root.left, level + 1, index - 1);
 
    // right child call
    addConsideringGrid(root.right, level + 1, index + 1);
}
 
static List<int> diagonalSum(Node root)
{
    grid.Clear();
 
    // Function call
    addConsideringGrid(root, 0, 0);
    List<int> ans = new List<int>();
 
    // for different values of level - index
    // add te sum of those node to answer
    foreach (KeyValuePair<int,int> x in grid)
    {
        ans.Add(x.Value);
    }
    return ans;
}
 
// Driver code
public static void Main(String[] args)
{
 
    // build binary tree
    Node root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(9);
    root.left.right = newNode(6);
    root.right.left = newNode(4);
    root.right.right = newNode(5);
    root.right.left.right = newNode(7);
    root.right.left.left = newNode(12);
    root.left.right.left = newNode(11);
    root.left.left.right = newNode(10);
 
    // Function Call
    List<int> v = diagonalSum(root);
 
    // print the diagonal sums
    for (int i = 0; i < v.Count; i++)
        Console.Write(v[i] + " ");
  }
}
 
// This code is contributed by Rajput-Ji

Javascript

<script>
 
// Javascript Program to calculate the
// sum of diagonal nodes.
     
    // Node Structure
    class Node
    {
        // Function to create new node
        constructor(data)
        {
            this.data=data;
            this.left=null;
            this.right=null;
             
        }
         
    }
     
    // to map the node with level - index
    let  grid = new Map();
     
    // recursvise function to calculate
    // sum of elements
   // where level - index is same.
    function addConsideringGrid(root,level,index)
    {
        // if there is no child then return
    if (root == null)
        return;
  
    // add the element in the group of node
    // whose level - index is equal
    if(grid.has(level-index))
    {
         
        grid.set(level - index,grid.get(level-index) +
        (root.data));
    }
    else
    {
        grid.set(level-index, root.data);
    }
  
    // left child call
    addConsideringGrid(root.left, level + 1, index - 1);
  
    // right child call
    addConsideringGrid(root.right, level + 1, index + 1);   
    }
     
    function  diagonalSum(root)
    {
        // Function call
    addConsideringGrid(root, 0, 0);
    let ans = [];
  
    // for different values of level - index
    // add te sum of those node to answer
    for (let [key, value] of grid)
    {
        ans.push(value);
        
    }
    return ans;
    }
     
   // Driver code
   // build binary tree
    let root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(9);
    root.left.right = new Node(6);
    root.right.left = new Node(4);
    root.right.right = new Node(5);
    root.right.left.right = new Node(7);
    root.right.left.left = new Node(12);
    root.left.right.left = new Node(11);
    root.left.left.right = new Node(10);
        
    // Function Call
    let v = diagonalSum(root);
     
    // print the diagonal sums
    for (let i = 0; i < v.length; i++)
        document.write(v[i] + " ");
     
    // This code is contributed by unknown2108
     
</script>

Output:

9 19 42

Time Complexity- O(n)

Method – 3

No Need to used Map for extra space.

space – o(n), queue used for left node left element for later processing

time complexity – o(n)

Java

import java.util.*;
class GFG
{
 
// Node Structure
static class Node
{
    int data;
    Node left, right;
};
 
// to map the node with level - index
 
// Function to create new node
static Node newNode(int data)
{
    Node Node = new Node();
    Node.data = data;
    Node.left = Node.right = null;
    return Node;
}
 
 
 public static ArrayList <Integer> diagonalSum(Node root){
        //list for storing diagonal sum
        ArrayList <Integer> list = new ArrayList <Integer> ();
         
        //list for processng diagonal left while traversing right
        /*
               1
             2    3
                 4
           1->3 while moving diagonally right
           queue 2,4 // for processing later
        */
        Queue <Node> queue = new LinkedList <Node> ();
        int sum = 0; // sum of digoanl element
        int count = 0; // number of element in next  diagonal
        int last = 0; // Number of element left to traverse current diagonal
        while(root!=null){
            if(root.left!=null){ // queue left
                queue.add(root.left);
                count++; // count of next diagonal elements
            }
            sum += root.data;
            root = root.right; //move diagonally right
            if(root == null){ // all element of diagonal  is traversed
                if(!queue.isEmpty()){ // check queue for processing any left
                  root = queue.poll();
                }
                if(last == 0){ // new diagonal sum , traversal of all element in current diagonal done or not
                    list.add(sum);
                    sum = 0;
                    last = count; // keep element in one diagonal
                    count = 0;
                }
              last--;
            }
        }
        return list;
         
 }
// Driver code
public static void main(String[] args)
{
 
    // build binary tree
    Node root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(9);
    root.left.right = newNode(6);
    root.right.left = newNode(4);
    root.right.right = newNode(5);
    root.right.left.right = newNode(7);
    root.right.left.left = newNode(12);
    root.left.right.left = newNode(11);
    root.left.left.right = newNode(10);
 
    // Function Call
    ArrayList <Integer> v = diagonalSum(root);
 
    // print the diagonal sums
    for (int i = 0; i < v.size(); i++)
        System.out.print(v.get(i) + " ");
  }
}

This article is contributed by Abhishek Chaudhary. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

My Personal Notes

Related Articles

Related Articles

Diagonal Sum of a Binary Tree

Method 1

C++

Java

Python3

C#

Javascript

Method 2:

C++

Java

Python3

C#

Javascript

Java