Count pairs from an array having GCD equal to the minimum element in the pair
Last Updated :
18 Oct, 2021
Given an array arr[] consisting of N integers, the task is to find the number of pairs such that the GCD of any pair of array elements is the minimum element of that pair.
Examples:
Input: arr[ ] = {2, 3, 1, 2}
Output: 4
Explanation:
Below are the all possible pairs from the given array:
- (0, 1): The GCD of the pair formed by element at indices 0 and 2 is gcd(2, 1) = 1, which is equal to its minimum value of the pair {2, 1}.
- (0, 3): The GCD of the pair formed by element at indices 0 and 3 is gcd(2, 2) = 2, which is equal to its minimum value of the pair {2, 2}.
- (1, 2): The GCD of the pair formed by taking element at indices 1 and 2 is gcd(3, 1) = 1, which is equal to its minimum value of the pair {3, 1}.
- (2, 3): The GCD of the pair formed by taking element at indices 2 and 3 is gcd(1, 2) = 1, which is equal to its minimum value of the pair {1, 2}.
Therefore, there is a total of 4 possible pairs whose GCD is equal to their minimum element of the pair.
Input: arr[] = {4, 6}
Output: 0
Naive Approach: The simplest approach to solve the given problem is to generate all possible pairs from the given array and if there exists any pair whose GCD is equal to the minimum elements of that pair, then count that pair. After checking for all the pairs, print the value of count obtained as the result.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countPairs(int arr[], int N)
{
int count = 0;
for (int i = 0; i < N - 1; i++) {
for (int j = i + 1; j < N; j++) {
if (arr[i] % arr[j] == 0
|| arr[j] % arr[i] == 0) {
count++;
}
}
}
return count;
}
int main()
{
int arr[] = { 2, 3, 1, 2 };
int N = sizeof(arr) / sizeof(arr[0]);
cout << countPairs(arr, N);
return 0;
}
|
Java
import java.io.*;
import java.lang.*;
import java.util.*;
public class GFG {
static int countPairs(int arr[], int N)
{
int count = 0;
for (int i = 0; i < N - 1; i++) {
for (int j = i + 1; j < N; j++) {
if (arr[i] % arr[j] == 0
|| arr[j] % arr[i] == 0) {
count++;
}
}
}
return count;
}
public static void main(String[] args)
{
int arr[] = { 2, 3, 1, 2 };
int N = arr.length;
System.out.print(countPairs(arr, N));
}
}
|
Python3
def countPairs(arr, N):
count = 0
for i in range(N - 1):
for j in range(i + 1, N):
if (arr[i] % arr[j] == 0 or arr[j] % arr[i] == 0):
count += 1
return count
if __name__ == '__main__':
arr = [2, 3, 1, 2]
N = len(arr)
print (countPairs(arr, N))
|
C#
using System;
public class GFG {
static int countPairs(int[] arr, int N)
{
int count = 0;
for (int i = 0; i < N - 1; i++) {
for (int j = i + 1; j < N; j++) {
if (arr[i] % arr[j] == 0
|| arr[j] % arr[i] == 0) {
count++;
}
}
}
return count;
}
public static void Main(string[] args)
{
int[] arr = { 2, 3, 1, 2 };
int N = arr.Length;
Console.WriteLine(countPairs(arr, N));
}
}
|
Javascript
<script>
function countPairs(arr, N)
{
let count = 0;
for (let i = 0; i < N - 1; i++) {
for (let j = i + 1; j < N; j++) {
if (arr[i] % arr[j] == 0
|| arr[j] % arr[i] == 0) {
count++;
}
}
}
return count;
}
let arr = [ 2, 3, 1, 2 ];
let N = arr.length;
document.write(countPairs(arr, N));
</script>
|
Time Complexity: O(N2)
Auxiliary Space: O(1)
Efficient Approach: The above approach can be optimized based on the following observations:
- The minimum element of the pair should divide the maximum element of the pair, and it can be observed that element 1 can form a total of (N – 1) pairs.
- Every element can form
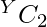 pair with itself where Y is the count of an array element.
pair with itself where Y is the count of an array element. - The idea is to traverse over the divisors of every array element and increment the count of pairs that can be formed by the frequencies of the divisors.
Follow the steps below to solve the problem:
- Initialize a variable, say res, that stores the resultant count.
- Initialize a map, say mp, that stores the count of every array element.
- Traverse the array arr[] and increment the count of arr[i] in mp.
- Iterate over the pairs of map mp and perform the following operations:
- Store the value of array element in a variable say X and frequency of that number in a variable Y.
- If the value of X is 1, then increment the value of res by (N – 1) and continue.
- Increment the value of res by (Y*(Y – 1))/2.
- Now, iterate over the divisors of the integer X using a variable j and increment the res by mp[j].
- After completing the above steps, print the value of res as the total count obtained.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int CountPairs(int arr[], int N)
{
int res = 0;
map<int, int> mp;
for (int i = 0; i < N; i++) {
mp[arr[i]]++;
}
for (auto p : mp) {
int x = p.first;
int y = p.second;
if (x == 1) {
res += N - 1;
continue;
}
res += (y * (y - 1)) / 2;
for (int j = 2;
j <= sqrt(x); j++) {
if (x % j == 0) {
res += mp[j];
if (j != x / j)
res += mp[x / j];
}
}
}
return res;
}
int main()
{
int arr[] = { 2, 3, 1, 2 };
int N = sizeof(arr) / sizeof(arr[0]);
cout << CountPairs(arr, N);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static int CountPairs(int arr[], int N)
{
int res = 0;
Map<Integer, Integer> mp = new HashMap<>();
for (int i = 0; i < N; i++) {
Integer c = mp.get(arr[i]);
mp.put(arr[i], (c == null) ? 1 : c + 1);
}
Iterator<Map.Entry<Integer, Integer>> itr = mp.entrySet().iterator();
while(itr.hasNext())
{
Map.Entry<Integer, Integer> entry = itr.next();
int x = (int)entry.getKey();
int y = (int)entry.getValue();
if (x == 1) {
res += N - 1;
continue;
}
res += (y * (y - 1)) / 2;
for (int j = 2; j <= Math.sqrt(x); j++) {
if (x % j == 0) {
res += mp.get(j);
if (j != x / j)
res += mp.get((int)x / j);
}
}
}
return res;
}
public static void main (String[] args) {
int arr[] = { 2, 3, 1, 2 };
int N = arr.length;
System.out.println(CountPairs(arr, N));
}
}
|
Python3
from math import sqrt
def CountPairs(arr, N):
res = 0
mp = {}
for i in range(N):
if (arr[i] in mp):
mp[arr[i]] += 1
else:
mp[arr[i]] = 1
for key, value in mp.items():
x = key
y = value
if (x == 1):
res += N - 1
continue
res += (y * (y - 1)) // 2
for j in range(2, int(sqrt(x)) + 1, 1):
if (x % j == 0):
res += mp[j]
if (j != x // j):
res += mp[x // j]
return res
if __name__ == '__main__':
arr = [ 2, 3, 1, 2 ]
N = len(arr)
print(CountPairs(arr, N))
|
C#
using System;
using System.Collections.Generic;
class GFG{
static int CountPairs(int []arr, int N)
{
int res = 0;
Dictionary<int,
int> mp = new Dictionary<int,
int>();
for(int i = 0; i < N; i++)
{
if (mp.ContainsKey(arr[i]))
mp[arr[i]]++;
else
mp.Add(arr[i], 1);
}
foreach(KeyValuePair<int, int> kvp in mp)
{
int x = kvp.Key;
int y = kvp.Value;
if (x == 1)
{
res += N - 1;
continue;
}
res += (y * (y - 1)) / 2;
for(int j = 2;
j <= Math.Sqrt(x); j++)
{
if (x % j == 0)
{
res += mp[j];
if (j != x / j)
res += mp[x / j];
}
}
}
return res;
}
public static void Main()
{
int []arr = { 2, 3, 1, 2 };
int N = arr.Length;
Console.Write(CountPairs(arr, N));
}
}
|
Javascript
<script>
function CountPairs(arr, N)
{
var res = 0;
var mp = new Map();
for (var i = 0; i < N; i++) {
if(mp.has(arr[i]))
{
mp.set(arr[i], mp.get(arr[i])+1);
}
else{
mp.set(arr[i], 1);
}
}
mp.forEach((value, key) => {
var x = key;
var y = value;
if (x == 1) {
res += N - 1;
}
res += parseInt((y * (y - 1)) / 2);
for (var j = 2;
j <= parseInt(Math.sqrt(x)); j++) {
if (x % j == 0) {
res += mp.get(j);
if (j != parseInt(x / j))
res += mp.get(parseInt(x / j));
}
}
});
return res;
}
var arr = [2, 3, 1, 2 ];
var N = arr.length;
document.write( CountPairs(arr, N));
</script>
|
Time Complexity: O(N*?M), where M is the maximum element of the array.
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...