Count of distinct Numbers that can be formed by chess knight in N moves on a mobile keypad

Given an integer N and a chess knight placed in mobile keypad. The task is to count the total distinct N digit numbers which can be formed by the chess knight with N moves. As the answer can be very large give the value of answer modulo 10⁹ + 7.

Note: In each move a chess knight can move 2 units horizontally and one unit vertically or two units vertically and one unit horizontally.

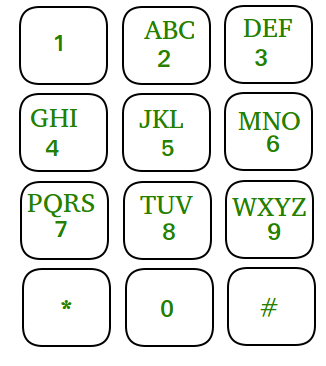
A demo mobile keypad is shown in image where ‘*’ and ‘#’ are not considered as part of a number.

Examples:

Input: N = 1
Output: 10
Explanation: Placing the knight over any numeric cell of the 10 cells is sufficient.

Input: N = 2
Output: 20
Explanation: All the valid number are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Approach: The idea is to find the possible cells that can be reached from a given cell for every cell and add all of them to find the answer. Follow the steps below to solve the problem:

• Initialize the vector v[10, 1], and temp[10].
• Iterate over the range [1, N) using the variable i and perform the following tasks:
  • Find the values for all cells in temp[] and then store them in vector v[].
• Initialize the variable sum as 0 to store the answer.
• Iterate over the range [0, 10) using the variable i and perform the following tasks:
  • Add the value of v[i] to the variable sum.
• After performing the above steps, print the value of sum as the answer.

Below is the implementation of the above approach.

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to find the total number of ways
int knightCalling(int N)
{
    int mod = 1000000007;

    // Base Case
    if (N == 1)
        return 10;
    vector<int> v(10, 1);
    vector<int> temp(10);

    // No cell can be reached from a
    // cell with value 5
    v[5] = 0;
    for (int i = 1; i < N; i++)
    {

        // Find the possible values from all cells
        temp[0] = (v[4] + v[6]) % mod;
        temp[1] = (v[6] + v[8]) % mod;
        temp[2] = (v[7] + v[9]) % mod;
        temp[3] = (v[4] + v[8]) % mod;
        temp[4] = (v[0] + v[3] + v[9]) % mod;
        temp[6] = (v[0] + v[1] + v[7]) % mod;
        temp[7] = (v[2] + v[6]) % mod;
        temp[8] = (v[1] + v[3]) % mod;
        temp[9] = (v[2] + v[4]) % mod;

        // Store them
        for (int j = 0; j < 10; j++)
            v[j] = temp[i];
    }

    // Find the answer
    int sum = 0;
    for (int i = 0; i < 10; i++)
        sum = (sum + v[i]) % mod;
    return sum;
}

// Driver Code
int main()
{
    int N = 2;
    cout << knightCalling(N);
}

// This code is contributed by Samim Hossain Mondal.

Java

// Java program for the above approach
import java.util.*;
class GFG{

// Function to find the total number of ways
static int knightCalling(int N)
{
    int mod = 1000000007;

    // Base Case
    if (N == 1)
        return 10;
    int []v = new int[10];
    int []temp = new int[10];
    Arrays.fill(v, 1);

    // No cell can be reached from a
    // cell with value 5
    v[5] = 0;
    for (int i = 1; i < N; i++)
    {

        // Find the possible values from all cells
        temp[0] = (v[4] + v[6]) % mod;
        temp[1] = (v[6] + v[8]) % mod;
        temp[2] = (v[7] + v[9]) % mod;
        temp[3] = (v[4] + v[8]) % mod;
        temp[4] = (v[0] + v[3] + v[9]) % mod;
        temp[6] = (v[0] + v[1] + v[7]) % mod;
        temp[7] = (v[2] + v[6]) % mod;
        temp[8] = (v[1] + v[3]) % mod;
        temp[9] = (v[2] + v[4]) % mod;

        // Store them
        for (int j = 0; j < 10; j++)
            v[i] = temp[i];
    }

    // Find the answer
    int sum = 0;
    for (int i = 0; i < 10; i++)
        sum = (sum + v[i]) % mod;
    return sum;
}

// Driver Code
public static void main(String[] args)
{
    int N = 2;
    System.out.print(knightCalling(N));
}
}

// This code is contributed by 29AjayKumar

Python3

# Python 3  program for the above approach

# Function to find the total number of ways
def knightCalling(N):

    mod = 1000000007

    # Base Case
    if (N == 1):
        return 10
    v = [1]*10
    temp = [0]*10

    # No cell can be reached from a
    # cell with value 5
    v[5] = 0
    for i in range(1, N):

        # Find the possible values from all cells
        temp[0] = (v[4] + v[6]) % mod
        temp[1] = (v[6] + v[8]) % mod
        temp[2] = (v[7] + v[9]) % mod
        temp[3] = (v[4] + v[8]) % mod
        temp[4] = (v[0] + v[3] + v[9]) % mod
        temp[6] = (v[0] + v[1] + v[7]) % mod
        temp[7] = (v[2] + v[6]) % mod
        temp[8] = (v[1] + v[3]) % mod
        temp[9] = (v[2] + v[4]) % mod

        # Store them
        for j in range(10):
            v[j] = temp[j]

    # Find the answer
    sum = 0
    for i in range(10):
        sum = (sum + v[i]) % mod
    return sum

# Driver Code
if __name__ == "__main__":

    N = 2
    print(knightCalling(N))

    # This code is contributed by ukasp.

C#

// C# program for the above approach
using System;
class GFG{

  // Function to find the total number of ways
  static int knightCalling(int N)
  {
    int mod = 1000000007;

    // Base Case
    if (N == 1)
      return 10;
    int []v = new int[10];
    int []temp = new int[10];
    for(int i = 0; i < 10; i++) {
      v[i] = 1;
    }

    // No cell can be reached from a
    // cell with value 5
    v[5] = 0;
    for (int i = 1; i < N; i++)
    {

      // Find the possible values from all cells
      temp[0] = (v[4] + v[6]) % mod;
      temp[1] = (v[6] + v[8]) % mod;
      temp[2] = (v[7] + v[9]) % mod;
      temp[3] = (v[4] + v[8]) % mod;
      temp[4] = (v[0] + v[3] + v[9]) % mod;
      temp[6] = (v[0] + v[1] + v[7]) % mod;
      temp[7] = (v[2] + v[6]) % mod;
      temp[8] = (v[1] + v[3]) % mod;
      temp[9] = (v[2] + v[4]) % mod;

      // Store them
      for (int j = 0; j < 10; j++)
        v[j] = temp[i];
    }

    // Find the answer
    int sum = 0;
    for (int i = 0; i < 10; i++)
      sum = (sum + v[i]) % mod;
    return sum;
  }

  // Driver Code
  public static void Main()
  {
    int N = 2;
    Console.Write(knightCalling(N));
  }
}

// This code is contributed by Samim Hossain Mondal.

Javascript

<script>
       // JavaScript code for the above approach

       // Function to find the total number of ways
       function knightCalling(N) {
           let mod = 1000000007;

           // Base Case
           if (N == 1)
               return 10;
           let v = new Array(10).fill(1)
           let temp = new Array(10).fill(0);

           // No cell can be reached from a
           // cell with value 5
           v[5] = 0;
           for (let i = 1; i < N; i++)
           {

               // Find the possible values from all cells
               temp[0] = (v[4] + v[6]) % mod;
               temp[1] = (v[6] + v[8]) % mod;
               temp[2] = (v[7] + v[9]) % mod;
               temp[3] = (v[4] + v[8]) % mod;
               temp[4] = (v[0] + v[3] + v[9]) % mod;
               temp[6] = (v[0] + v[1] + v[7]) % mod;
               temp[7] = (v[2] + v[6]) % mod;
               temp[8] = (v[1] + v[3]) % mod;
               temp[9] = (v[2] + v[4]) % mod;

               // Store them
               for (let i = 0; i < 10; i++)
                   v[i] = temp[i];
           }

           // Find the answer
           let sum = 0;
           for (let i = 0; i < 10; i++)
               sum = (sum + v[i]) % mod;
           return sum;
       }

       // Driver Code
       let N = 2;
       document.write(knightCalling(N));

 // This code is contributed by Potta Lokesh
   </script>

Output

20

Time Complexity: O(N)
Auxiliary Space: O(1)