Given the mobile numeric keypad. You can only press buttons that are up, left, right or down to the current button or can choose to press the same button again. Round corner buttons (i.e. * and # ) are invalid moves.
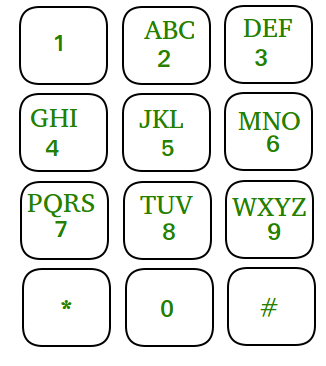
Given a number N, You have to find the distinct numbers of length N you can dial by starting from any number from 0-9, under the constraint that you can only move up, left, right or down from the last number you pressed, or you can choose to press the same button again.
Examples:
Input: N = 1
Output: 10
0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 are the possible numbers.
Input: N = 2
Output: 36
All the possible numbers are 00, 08, 11, 12, 14, 21, 22, 23, 25, …
Input: N = 6
Output: 7990
Approach: We have seen many solutions to solve this problem here.
Let Xni be the count of n digit numbers ending with i.
So, by this notation,
X10 = 1 which is {0}
X11 = 1 which is {1}
X12 = 1 which is {2}
X13 = 1 which is {3}
and
X20 = 2 which are {00, 80}
X21 = 3 which are {11, 21, 41}
X22 = 4 which are {22, 12, 32, 52}
The central idea is, if you know Xni, what information you can get about Xn + 1j
Let’s see with the help of an example:
Suppose we know, X21 = 3 which are {11, 21, 41}
Because the last digit of all these numbers is 1, let’s look at the possible moves that we can have from 1:
- Pressing 1 again.
- Pressing 2 (moving right).
- Pressing 4 (moving down)
Now we can pick any element from our set {11, 21, 41} and make any valid move:
- {111, 211, 411} can be achieved with the first move.
- {112, 212, 412} with the second move.
- And {114, 214, 414} with the third.
We can see that making any possible move, we get the set of the same size with every move. i.e. There were 3 elements in the set of two digits numbers ending with 1, we got set of the same size(3) with every possible move from 1.
So, it can be seen that X21 contributes in 3 digits numbers as follow:
X31 += X21
X32 += X21
X34 += X21
So, in general, if we know about Xni, we know the count it contributes to Xn+1j, where j is every possible move from i.
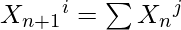
where 0<=j<=9 and from j we can have a valid to i
The idea is to first enumerate all possible directions from every given key, and maintain an array of 10 elements where the element at each index store the count of numbers ending with that index.
E.g. Initial values of array are:
Value 1 1 1 1 1 1 1 1 1 1
Index 0 1 2 3 4 5 6 7 8 9
And initial result for n = 1 is Sum of all elements in the array i.e 1+1+1+1+1+1+1+1+1+1 = 10, there are 10 number of 1 digit that can be dialed.
How to update the array for n > 1?
Let’s enumerate all directions for all given numbers first:
| From | To (Possible moves) |
|---|
| 0 | 0, 8 |
| 1 | 1, 2, 4 |
| 2 | 2, 1, 3, 5 |
| 3 | 3, 6, 2 |
| 4 | 4, 1, 7, 5 |
| 5 | 5, 4, 6, 2, 8 |
| 6 | 6, 3, 5, 9 |
| 7 | 7, 4, 8 |
| 8 | 8, 5, 0, 7, 9 |
| 9 | 9, 6, 8 |
The first row of the table listed above indicates that, if the last digit in the number was zero, we can move to 0 or 8.
Let’s have a detailed look at the approach for N = 2
For N = 1, Arr[10] is {1, 1, 1, 1, 1, 1, 1, 1, 1, 1} indicating there are Arr[i] numbers ending with index i
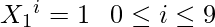
Lets Create a new array, say Arr2[10] = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
Now, for 0, possible moves are 0 and 8.
we already know
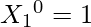
That would contribute 1 to {0, 8} i.e.
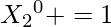
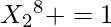
Arr2[10] = {1, 0, 0, 0, 0, 0, 0, 0, 1, 0}
For 1, Possible moves are 1, 2, 4
we already know
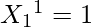
That would contribute 1 to {1, 2, 4} i.e.
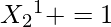
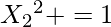
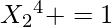
Arr2[10] = {1, 1, 1, 0, 1, 0, 0, 0, 1, 0}
For 2, Possible moves are 2, 1, 3, 4
we already know
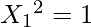
That would contribute 1 to {2, 1, 3, 4}
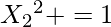
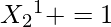
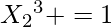
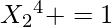
Arr2[10] = {1, 2, 2, 1, 1, 0, 0, 0, 1, 0}
and so on ….
Arr2[10] = {2, 3, 4, 3, 4, 5, 4, 3, 5, 3}
Sum = 2+3+4+3+4+5+4+3+5+3 = 36 (For N=2)
Arr2 now holds the values for 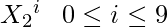 and can be considered as starting point for n=3 and the process continues.
and can be considered as starting point for n=3 and the process continues.
Below is the implementation of the above approach:
C++
#include <iostream>
#include <list>
using namespace std;
#define MAX 10
int getCount(int n)
{
list<int> mylist[MAX];
mylist[0].assign({ 0, 8 });
mylist[1].assign({ 1, 2, 4 });
mylist[2].assign({ 2, 1, 3, 5 });
mylist[3].assign({ 3, 6, 2 });
mylist[4].assign({ 4, 1, 7, 5 });
mylist[5].assign({ 5, 4, 6, 2, 8 });
mylist[6].assign({ 6, 3, 5, 9 });
mylist[7].assign({ 7, 4, 8 });
mylist[8].assign({ 8, 5, 0, 7, 9 });
mylist[9].assign({ 9, 6, 8 });
int Arr[MAX] = { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 };
for (int i = 2; i <= n; i++) {
int Arr2[MAX] = { 0 };
for (int j = 0; j < MAX; j++) {
for (int x : mylist[j]) {
Arr2[x] += Arr[j];
}
}
for (int j = 0; j < MAX; j++)
Arr[j] = Arr2[j];
}
int sum = 0;
for (int i = 0; i < MAX; i++)
sum += Arr[i];
return sum;
}
int main()
{
int n = 2;
cout << getCount(n);
return 0;
}
|
Java
class GFG
{
static int MAX = 10;
static int getCount(int n)
{
int [][] list = new int[MAX][];
list[0] = new int [] { 0, 8 };
list[1] = new int [] { 1, 2, 4 };
list[2] = new int [] { 2, 1, 3, 5 };
list[3] = new int [] { 3, 6, 2 };
list[4] = new int [] { 4, 1, 7, 5 };
list[5] = new int [] { 5, 4, 6, 2, 8 };
list[6] = new int [] { 6, 3, 5, 9 };
list[7] = new int [] { 7, 4, 8 };
list[8] = new int [] { 8, 5, 0, 7, 9 };
list[9] = new int [] { 9, 6, 8 };
int Arr[] = new int [] { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 };
for (int i = 2; i <= n; i++)
{
int Arr2[] = new int [MAX];
for (int j = 0; j < MAX; j++)
{
for (int x = 0; x < list[j].length; x++)
{
Arr2[list[j][x]] += Arr[j];
}
}
for (int j = 0; j < MAX; j++)
Arr[j] = Arr2[j];
}
int sum = 0;
for (int i = 0; i < MAX; i++)
sum += Arr[i];
return sum;
}
public static void main (String[] args)
{
int n = 2;
System.out.println(getCount(n));
}
}
|
Python3
MAX = 10
def getCount(n):
global MAX
mylist = [[] for i in range(MAX)]
mylist[0] = [ 0, 8 ]
mylist[1] = [ 1, 2, 4 ]
mylist[2] = [ 2, 1, 3, 5 ]
mylist[3] = [ 3, 6, 2 ]
mylist[4] = [ 4, 1, 7, 5 ]
mylist[5] = [ 5, 4, 6, 2, 8 ]
mylist[6] = [ 6, 3, 5, 9 ]
mylist[7] = [ 7, 4, 8 ]
mylist[8] = [ 8, 5, 0, 7, 9 ]
mylist[9] = [ 9, 6, 8 ]
Arr = [1 for i in range(MAX)]
for i in range(2,n+1):
Arr2 = [0 for i in range(MAX)]
for j in range(MAX):
for x in mylist[j]:
Arr2[x] += Arr[j]
for j in range(MAX):
Arr[j] = Arr2[j]
sum = 0
for i in range(MAX):
sum += Arr[i]
return sum
n = 2
print(getCount(n))
|
C#
using System;
class GFG
{
static int MAX = 10;
static int getCount(int n)
{
int [][] list = new int[MAX][];
list[0] = new int [] { 0, 8 };
list[1] = new int [] { 1, 2, 4 };
list[2] = new int [] { 2, 1, 3, 5 };
list[3] = new int [] { 3, 6, 2 };
list[4] = new int [] { 4, 1, 7, 5 };
list[5] = new int [] { 5, 4, 6, 2, 8 };
list[6] = new int [] { 6, 3, 5, 9 };
list[7] = new int [] { 7, 4, 8 };
list[8] = new int [] { 8, 5, 0, 7, 9 };
list[9] = new int [] { 9, 6, 8 };
int [] Arr = new int [] { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 };
for (int i = 2; i <= n; i++)
{
int [] Arr2 = new int [MAX];
for (int j = 0; j < MAX; j++)
{
for (int x = 0; x < list[j].Length; x++)
{
Arr2[list[j][x]] += Arr[j];
}
}
for (int j = 0; j < MAX; j++)
Arr[j] = Arr2[j];
}
int sum = 0;
for (int i = 0; i < MAX; i++)
sum += Arr[i];
return sum;
}
public static void Main ()
{
int n = 2;
Console.WriteLine(getCount(n));
}
}
|
Javascript
<script>
let MAX = 10
function getCount(n)
{
let mylist = new Array(MAX).fill(new Array());
mylist[0] = [ 0, 8 ];
mylist[1] = [ 1, 2, 4 ];
mylist[2] = [ 2, 1, 3, 5 ];
mylist[3] = [ 3, 6, 2 ];
mylist[4] = [ 4, 1, 7, 5 ];
mylist[5] = [ 5, 4, 6, 2, 8 ];
mylist[6] = [ 6, 3, 5, 9 ];
mylist[7] = [ 7, 4, 8 ];
mylist[8] = [ 8, 5, 0, 7, 9 ];
mylist[9] = [ 9, 6, 8 ];
let Arr = new Array(MAX).fill(1);
for (let i = 2; i <= n; i++) {
let Arr2 = new Array(MAX).fill(0);
for (let j = 0; j < MAX; j++) {
for (let x in mylist[j]) {
Arr2[x] += Arr[j];
}
}
for (let j = 0; j < MAX; j++)
Arr[j] = Arr2[j];
}
let sum = 0;
for (let i = 0; i < MAX; i++)
sum += Arr[i];
return sum;
}
let n = 2;
document.write(getCount(n),"</br>");
</script>
|
Time Complexity: O(N)
Space Complexity: O(1)
Share your thoughts in the comments
Please Login to comment...