Floyd’s Cycle Finding Algorithm
Last Updated :
10 May, 2023
Floyd’s cycle finding algorithm or Hare-Tortoise algorithm is a pointer algorithm that uses only two pointers, moving through the sequence at different speeds. This algorithm is used to find a loop in a linked list. It uses two pointers one moving twice as fast as the other one. The faster one is called the fast pointer and the other one is called the slow pointer.
How Does Floyd’s Cycle Finding Algorithm Works?
While traversing the linked list one of these things will occur-
- The Fast pointer may reach the end (NULL) this shows that there is no loop in the linked list.
- The Fast pointer again catches the slow pointer at some time therefore a loop exists in the linked list.
Example:


Pseudocode:
- Initialize two-pointers and start traversing the linked list.
- Move the slow pointer by one position.
- Move the fast pointer by two positions.
- If both pointers meet at some point then a loop exists and if the fast pointer meets the end position then no loop exists.
Below is the C++ program to implement the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* next;
Node(int data)
{
this->data = data;
next = NULL;
}
};
Node* head = NULL;
class Linkedlist {
public:
void insert(int value)
{
Node* newNode = new Node(value);
if (head == NULL)
head = newNode;
else {
newNode->next = head;
head = newNode;
}
}
bool detectLoop()
{
Node *slowPointer = head,
*fastPointer = head;
while (slowPointer != NULL
&& fastPointer != NULL
&& fastPointer->next != NULL) {
slowPointer = slowPointer->next;
fastPointer = fastPointer->next->next;
if (slowPointer == fastPointer)
return 1;
}
return 0;
}
};
int main()
{
Linkedlist l1;
l1.insert(10);
l1.insert(20);
l1.insert(30);
l1.insert(40);
l1.insert(50);
Node* temp = head;
while (temp->next != NULL)
temp = temp->next;
temp->next = head;
if (l1.detectLoop())
cout << "Loop exists in the"
<< " Linked List" << endl;
else
cout << "Loop does not exists "
<< "in the Linked List" << endl;
return 0;
}
|
Java
import java.util.*;
class GFG{
static class Node {
int data;
Node next;
Node(int data)
{
this.data = data;
next = null;
}
};
static Node head = null;
static class Linkedlist {
void insert(int value)
{
Node newNode = new Node(value);
if (head == null)
head = newNode;
else {
newNode.next = head;
head = newNode;
}
}
boolean detectLoop()
{
Node slowPointer = head,
fastPointer = head;
while (slowPointer != null
&& fastPointer != null
&& fastPointer.next != null) {
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
if (slowPointer == fastPointer)
return true;
}
return false;
}
}
public static void main(String[] args)
{
Linkedlist l1 = new Linkedlist();
l1.insert(10);
l1.insert(20);
l1.insert(30);
l1.insert(40);
l1.insert(50);
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = head;
if (l1.detectLoop())
System.out.print("Loop exists in the"
+ " Linked List" +"\n");
else
System.out.print("Loop does not exists "
+ "in the Linked List" +"\n");
}
}
|
Python3
class Node:
def __init__(self, d):
self.data = d
self.next = None
head = None
def detectLoop(head):
slowPointer = head
fastPointer = head
while (slowPointer != None
and fastPointer != None
and fastPointer.next != None):
slowPointer = slowPointer.next
fastPointer = fastPointer.next.next
if (slowPointer == fastPointer):
return 1
return 0
head = Node(10)
head.next = Node(20)
head.next.next = Node(30)
head.next.next.next = Node(40)
head.next.next.next.next = Node(50)
temp = head
while (temp.next != None):
temp = temp.next
temp.next = head
if (detectLoop(head)):
print("Loop exists in the Linked List")
else:
print("Loop does not exists in the Linked List")
|
C#
using System;
using System.Collections.Generic;
public class GFG {
public class Node {
public int data;
public Node next;
public Node(int data) {
this.data = data;
next = null;
}
};
static Node head = null;
public class Linkedlist
{
public void insert(int value) {
Node newNode = new Node(value);
if (head == null)
head = newNode;
else {
newNode.next = head;
head = newNode;
}
}
public bool detectLoop() {
Node slowPointer = head, fastPointer = head;
while (slowPointer != null && fastPointer != null &&
fastPointer.next != null)
{
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
if (slowPointer == fastPointer)
return true;
}
return false;
}
}
public static void Main(String[] args) {
Linkedlist l1 = new Linkedlist();
l1.insert(10);
l1.insert(20);
l1.insert(30);
l1.insert(40);
l1.insert(50);
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = head;
if (l1.detectLoop())
Console.Write("Loop exists in the" + " Linked List" + "\n");
else
Console.Write("Loop does not exists " + "in the Linked List" + "\n");
}
}
|
Javascript
<script>
class Node
{
constructor(d)
{
this.data = d;
this.next = null;
}
}
let head = null;
function detectLoop(head) {
let slowPointer = head;
let fastPointer = head;
while (slowPointer != null
&& fastPointer != null
&& fastPointer.next != null) {
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
if (slowPointer == fastPointer)
return 1;
}
return 0;
}
head = new Node(10);
head.next = new Node(20);
head.next.next = new Node(30);
head.next.next.next = new Node(40);
head.next.next.next.next = new Node(50);
let temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = head;
if (detectLoop(head))
document.write("Loop exists in the Linked List" + "<br>");
else
document.write("Loop does not exists in the Linked List" + "<br>");
</script>
|
Output
Loop exists in the Linked List
Time complexity: O(n), as the loop is traversed once.
Auxiliary Space: O(1), only two pointers are used therefore constant space complexity.
Why Does Floyd’s Algorithm Works?
Let us consider an example:
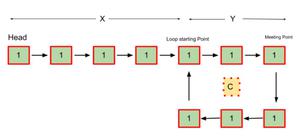
X = Distance between the head(starting) to the loop starting point.
Y = Distance between the loop starting point and the first meeting point of both the pointers.
C = The distance of the loop
- So before both the pointer meets-
The slow pointer has traveled X + Y + s * C distance, where s is any positive constant number.
The fast pointer has traveled X + Y + f * C distance, where f is any positive constant number.
- Since the fast pointer is moving twice as fast as the slow pointer, we can say that the fast pointer covered twice the distance the slow pointer covered. Therefore-
X + Y + f * C = 2 * (X + Y + s * C)
X + Y = f * C – 2 * s * C
We can say that,
f * C – 2 * s * C = (some integer) * C
= K * C
Thus,
X + Y = K * C – ( 1 )
X = K * C – Y – ( 2 )
Where K is some positive constant.
- Now if reset the slow pointer to the head(starting position) and move both fast and slow pointer by one unit at a time, one can observe from 1st and 2nd equation that both of them will meet after traveling X distance at the starting of the loop because after resetting the slow pointer and moving it X distance, at the same time from loop meeting point the fast pointer will also travel K * C – Y distance(because it already has traveled Y distance).
- From equation (2) one can say that X = K * C – Y therefore, both the pointers will travel the distance X i.e. same distance after the pink node at some point to meet at the starting point of the cycle.
- Here, by some point, it means that the fast pointer can complete the K * C distance out of which it has already covered the Y distance.
- Conclusively, we find that slow pointer moves 1 step at a time while fast pointer moves 2 steps at a time so the fast pointer catches or surpasses slow pointer if there is a loop, just like start <end in Binary Search. Else if there exists no loop then fast pointer reaches the NULL before than slow (and wins the race: tortoise ->slow pointer and hare/rabbit->fast pointer).
Below is the C++ program to implement the above approach-
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* next;
Node(int data)
{
this->data = data;
next = NULL;
}
};
Node* head = NULL;
class Linkedlist {
public:
void insert(int value)
{
Node* newNode = new Node(value);
if (head == NULL)
head = newNode;
else {
newNode->next = head;
head = newNode;
}
}
Node* detectLoop()
{
if(head==NULL || head->next==NULL){
return NULL;
}
Node *slowPointer = head, *fastPointer = head;
while (slowPointer != NULL && fastPointer != NULL
&& fastPointer->next != NULL) {
slowPointer = slowPointer->next;
fastPointer = fastPointer->next->next;
if (slowPointer == fastPointer)
break;
}
if (slowPointer != fastPointer)
return NULL;
slowPointer = head;
while (slowPointer != fastPointer) {
slowPointer = slowPointer->next;
fastPointer = fastPointer->next;
}
return slowPointer;
}
};
int main()
{
Linkedlist l1;
l1.insert(10);
l1.insert(20);
l1.insert(30);
l1.insert(40);
l1.insert(50);
Node* temp = head;
while (temp->next != NULL)
temp = temp->next;
temp->next = head;
Node* loopStart = l1.detectLoop();
if (loopStart == NULL)
cout << "Loop does not exists" << endl;
else {
cout << "Loop does exists and starts from "
<< loopStart->data << endl;
}
return 0;
}
|
Java
import java.util.*;
public class GFG {
static class Node {
int data;
Node next;
Node(int data)
{
this.data = data;
next = null;
}
}
static Node head = null;
static class Linkedlist {
void insert(int value)
{
Node newNode = new Node(value);
if (head == null)
head = newNode;
else {
newNode.next = head;
head = newNode;
}
}
public Node detectLoop()
{
Node slowPointer = head, fastPointer = head;
while (slowPointer != null
&& fastPointer != null
&& fastPointer.next != null) {
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
if (slowPointer == fastPointer)
break;
}
if (slowPointer != fastPointer)
return null;
slowPointer = head;
while (slowPointer != fastPointer) {
slowPointer = slowPointer.next;
fastPointer = fastPointer.next;
}
return slowPointer;
}
}
public static void main(String[] args)
{
Linkedlist l1 = new Linkedlist();
l1.insert(10);
l1.insert(20);
l1.insert(30);
l1.insert(40);
l1.insert(50);
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = head;
Node loopStart = l1.detectLoop();
if (loopStart == null)
System.out.println("Loop does not exists");
else {
System.out.println(
"Loop does exists and starts from "
+ loopStart.data);
}
}
}
|
Python3
class Node:
def __init__(self, d):
self.data = d
self.next = None
head = None
def detectLoop(head):
slowPointer = head
fastPointer = head
while (slowPointer != None
and fastPointer != None
and fastPointer.next != None):
slowPointer = slowPointer.next
fastPointer = fastPointer.next.next
if (slowPointer == fastPointer):
break
if (slowPointer != fastPointer):
return None
slowPointer = head
while (slowPointer != fastPointer):
slowPointer = slowPointer.next
fastPointer = fastPointer.next
return slowPointer
head = Node(50)
head.next = Node(40)
head.next.next = Node(30)
head.next.next.next = Node(20)
head.next.next.next.next = Node(10)
temp = head
while (temp.next != None):
temp = temp.next
temp.next = head
loopStart = detectLoop(head)
if (loopStart == None):
print("Loop does not exists")
else:
print(f"Loop does exists and starts from {loopStart.data}")
|
C#
using System;
public class GFG
{
public class Node
{
public int data;
public Node next;
public Node(int data)
{
this.data = data;
next = null;
}
}
static Node head = null;
public class Linkedlist
{
public void insert(int value)
{
Node newNode = new Node(value);
if (head == null)
head = newNode;
else
{
newNode.next = head;
head = newNode;
}
}
public Node detectLoop()
{
Node slowPointer = head, fastPointer = head;
while (slowPointer != null
&& fastPointer != null
&& fastPointer.next != null)
{
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
if (slowPointer == fastPointer)
break;
}
if (slowPointer != fastPointer)
return null;
slowPointer = head;
while (slowPointer != fastPointer)
{
slowPointer = slowPointer.next;
fastPointer = fastPointer.next;
}
return slowPointer;
}
}
public static void Main()
{
Linkedlist l1 = new Linkedlist();
l1.insert(10);
l1.insert(20);
l1.insert(30);
l1.insert(40);
l1.insert(50);
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = head;
Node loopStart = l1.detectLoop();
if (loopStart == null)
Console.WriteLine("Loop does not exists");
else
{
Console.WriteLine(
"Loop does exists and starts from "
+ loopStart.data);
}
}
}
|
Javascript
class Node
{
constructor(d)
{
this.data = d;
this.next = null;
}
}
let head = null;
function detectLoop(head) {
let slowPointer = head, fastPointer = head;
while(slowPointer!=null && fastPointer!=null && fastPointer.next!=null){
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
if(slowPointer==fastPointer){
break;
}
}
if(slowPointer!=fastPointer){
return null;
}
slowPointer = head;
while(slowPointer!=fastPointer){
slowPointer = slowPointer.next;
fastPointer = fastPointer.next;
}
return slowPointer;
}
head = new Node(50);
head.next = new Node(40);
head.next.next = new Node(30);
head.next.next.next = new Node(20);
head.next.next.next.next = new Node(10);
let temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = head;
let loopStart = detectLoop(head);
if (loopStart==null)
console.log("Loop does not exists" + "<br>");
else
console.log("Loop does exists and starts from " + loopStart.data);
|
Output
Loop does exists and starts from 50
Time complexity: O(n), as we have traversed the loop once and then traveled X distance.
Auxiliary space: O(1), as only pointers are used therefore constant space complexity.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...