Count number of step required to reduce N to 1 by following certain rule
Last Updated :
30 Aug, 2022
Given a positive integer 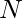 . Find the number of steps required to minimize it to 1. In a single step N either got reduced to half if it is power of 2 else N is reduced to difference of N and its nearest power of 2 which is smaller than N.
. Find the number of steps required to minimize it to 1. In a single step N either got reduced to half if it is power of 2 else N is reduced to difference of N and its nearest power of 2 which is smaller than N.
Examples:
Input : N = 2
Output : 1
Input : N = 20
Output : 3
Simple Approach: As per question a very simple and brute force approach is to iterate over N until it got reduced to 1, where reduction involve two cases:
- N is power of 2 : reduce n to n/2
- N is not power of 2: reduce n to n – (2^log2(n))
Efficient approach: Before proceeding to actual result lets have a look over bit representation of an integer n as per problem statement.
- When an integer is power of 2: In this case bit -representation includes only one set bit and that too is left most. Hence log2(n) i.e. bit-position minus One is the number of step required to reduce it to n. Which is also equal to number of set bit in n-1.
- When an integer is not power of 2:The remainder of n – 2^(log2(n)) is equal to integer which can be obtained by un-setting the left most set bit. Hence, one set bit removal count as one step in this case.
Hence the actual answer for steps required to reduce n is equal to number of set bits in n-1. Which can be easily calculated either by using the loop or any of method described in the post: Count Set bits in an Integer.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
int stepRequired(int n)
{
return __builtin_popcount(n - 1);
}
int main()
{
int n = 94;
cout << stepRequired(n) << endl;
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int stepRequired(int n)
{
return Integer.bitCount(n - 1);
}
public static void main(String []args)
{
int n = 94;
System.out.println(stepRequired(n));
}
}
|
Python3
def stepRequired(n) :
return bin(94).count('1')
if __name__ == "__main__" :
n = 94
print(stepRequired(n))
|
C#
using System;
class GFG
{
static int countSetBits(int n)
{
if (n == 0)
return 0;
else
return (n & 1) + countSetBits(n >> 1);
}
static int stepRequired(int n)
{
return countSetBits(n - 1);
}
public static void Main()
{
int n = 94;
Console.WriteLine(stepRequired(n));
}
}
|
PHP
<?php
function countSetBits($n)
{
if ($n == 0)
return 0;
else
return 1 +
countSetBits($n &
($n - 1));
}
function stepRequired($n)
{
return countSetBits($n - 1);
}
$n = 94;
echo stepRequired($n);
?>
|
Javascript
<script>
function countSetBits(n)
{
if (n == 0)
return 0;
else
return (n & 1) + countSetBits(n >> 1);
}
function stepRequired(n)
{
return countSetBits(n - 1);
}
let n = 94;
document.write(stepRequired(n));
</script>
|
Time Complexity: O(1) as constant time is taken.
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...