Given a number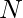 
. Reduce this number to zero by subtracting the number by it’s most significant digit(Left most digit) at every step. The task is to count the number of steps it takes to be reduced to zero.
Examples:
Input: 14
Output: 6
Steps:
14 - 1 = 13
13 - 1 = 12
12 - 1 = 11
11 - 1 = 10
10 - 1 = 9
9 - 9 = 0
Input: 20
Output: 12
Numbers after series of steps:
20, 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 0
Naive Approach: A naive approach is to reduce the number by its first digit step-wise and find the count of steps, but the time complexity will be huge if a large number is provided.
Efficient Approach: The main idea of the efficient approach is to reduce the number of steps in the naive approach. We can skip the steps whose leading digits are the same in consecutive numbers, and count them. The algorithm of skipping those numbers with the same leading digits is as follows:
- Let the number be last, count the digits in last and reduce it by 1, because the smallest number with same leading digit with the same count of digits will have that number of zeros in it.
- Find the first digit of the number of last, by last/count.
- Hence the smallest number of same number of count of digits with same leading number will be [first digit * (count-1)]
- the number of steps skipped can be achieved by [(last-smallest number)/first digit].
- Hence the next number last will be last – (first*skipped)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countdig(int m)
{
if (m == 0)
return 0;
else
return 1 + countdig(m / 10);
}
int countSteps(int x)
{
int c = 0;
int last = x;
while (last) {
int digits = countdig(last);
digits -= 1;
int divisor = pow(10, digits);
int first = last / divisor;
int lastnumber = first * divisor;
int skipped = (last - lastnumber) / first;
skipped += 1;
c += skipped;
last = last - (first * skipped);
}
return c;
}
int main()
{
int n = 14;
cout << countSteps(n);
return 0;
}
|
Java
class GFG{
static int countdig(int m)
{
if (m == 0)
return 0;
else
return 1 + countdig(m / 10);
}
static int countSteps(int x)
{
int c = 0;
int last = x;
while (last>0) {
int digits = countdig(last);
digits -= 1;
int divisor = (int)Math.pow(10, digits);
int first = last / divisor;
int lastnumber = first * divisor;
int skipped = (last - lastnumber) / first;
skipped += 1;
c += skipped;
last = last - (first * skipped);
}
return c;
}
public static void main(String[] args)
{
int n = 14;
System.out.println(countSteps(n));
}
}
|
Python 3
def countdig(m) :
if (m == 0) :
return 0
else :
return 1 + countdig(m // 10)
def countSteps(x) :
c = 0
last = x
while (last) :
digits = countdig(last)
digits -= 1
divisor = pow(10, digits)
first = last // divisor
lastnumber = first * divisor
skipped = (last - lastnumber) // first
skipped += 1
c += skipped
last = last - (first * skipped)
return c
n = 14
print(countSteps(n))
|
C#
using System;
class GFG{
static int countdig(int m)
{
if (m == 0)
return 0;
else
return 1 + countdig(m / 10);
}
static int countSteps(int x)
{
int c = 0;
int last = x;
while (last>0) {
int digits = countdig(last);
digits -= 1;
int divisor = (int)Math.Pow(10, digits);
int first = last / divisor;
int lastnumber = first * divisor;
int skipped = (last - lastnumber) / first;
skipped += 1;
c += skipped;
last = last - (first * skipped);
}
return c;
}
static void Main()
{
int n = 14;
Console.WriteLine(countSteps(n));
}
}
|
PHP
<?php
function countdig($m)
{
if ($m == 0)
return 0;
else
return 1 + countdig( (int)($m / 10));
}
function countSteps($x)
{
$c = 0;
$last = $x;
while ($last)
{
$digits = countdig($last);
$digits -= 1;
$divisor = pow(10, $digits);
$first = (int)($last / $divisor);
$lastnumber = $first * $divisor;
$skipped = ($last - $lastnumber) / $first;
$skipped += 1;
$c += $skipped;
$last = $last - ($first * $skipped);
}
return $c;
}
$n = 14;
echo countSteps($n);
|
Javascript
<script>
function countdig(m) {
if (m == 0)
return 0;
else
return 1 + countdig(parseInt(m / 10));
}
function countSteps(x) {
var c =0;
var last = x;
while (last > 0) {
var digits = countdig(last);
digits -= 1;
var divisor = parseInt( Math.pow(10, digits));
var first = parseInt(last / divisor);
var lastnumber = first * divisor;
var skipped = parseInt((last - lastnumber) / first);
skipped += 1;
c += skipped;
last = last - (first * skipped);
}
return c;
}
var n = 14;
document.write(countSteps(n));
</script>
|
Time Complexity: O(N*logN), as in the worst case the while loop will traverse N times and in each traversal we are using power function and countdig function, each of these will cost logN time, so the effective time complexity of the program will be O (N*logN).
Auxiliary Space: O(1), as we are not using any extra space.