Given the root of a Complete Binary Tree consisting of N nodes, the task is to find the total number of nodes in the given Binary Tree.
Examples:
Input:
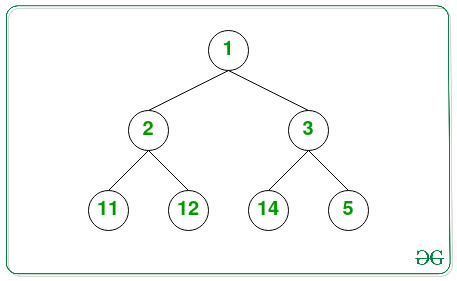
Output: 7
Input:
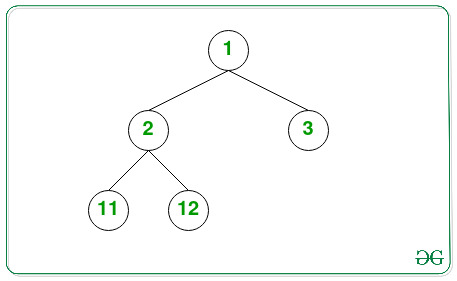
Output: 5
Native Approach: The simple approach to solving the given tree is to perform the DFS Traversal on the given tree and count the number of nodes in it. After traversal, print the total count of nodes obtained.
C++
#include <bits/stdc++.h>
using namespace std;
class node {
public:
int data;
node* left;
node* right;
};
int totalNodes(node* root)
{
if (root == NULL)
return 0;
int l = totalNodes(root->left);
int r = totalNodes(root->right);
return 1 + l + r;
}
node* newNode(int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
int main()
{
node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(9);
root->right->right = newNode(8);
root->left->left->left = newNode(6);
root->left->left->right = newNode(7);
cout << totalNodes(root);
return 0;
}
|
Java
import java.io.*;
class GFG {
static class node
{
public int data;
public node left, right;
public node(){
data = 0;
left = right = null;
}
}
static int totalNodes(node root)
{
if (root == null)
return 0;
int l = totalNodes(root.left);
int r = totalNodes(root.right);
return 1 + l + r;
}
static node newNode(int data)
{
node temp = new node();
temp.data = data;
temp.left = temp.right = null;
return temp;
}
public static void main(String args[])
{
node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.left = newNode(9);
root.right.right = newNode(8);
root.left.left.left = newNode(6);
root.left.left.right = newNode(7);
System.out.println(totalNodes(root));
}
}
|
Python
class node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
def totalNodes(root):
if(root == None):
return 0
l = totalNodes(root.left)
r = totalNodes(root.right)
return 1 + l + r
def newNode(data):
Node = node(data)
return Node
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(4)
root.left.right = newNode(5)
root.right.left = newNode(9)
root.right.right = newNode(8)
root.left.left.left = newNode(6)
root.left.left.right = newNode(7)
print(totalNodes(root))
|
C#
using System;
class GFG
{
public class node
{
public int data;
public node left, right;
public node()
{
data = 0;
left = right = null;
}
}
static int totalNodes(node root)
{
if (root == null)
return 0;
int l = totalNodes(root.left);
int r = totalNodes(root.right);
return 1 + l + r;
}
static node newNode(int data)
{
node temp = new node();
temp.data = data;
temp.left = temp.right = null;
return temp;
}
static void Main(string[] args)
{
node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.left = newNode(9);
root.right.right = newNode(8);
root.left.left.left = newNode(6);
root.left.left.right = newNode(7);
Console.WriteLine(totalNodes(root));
}
}
|
Javascript
<script>
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
function totalNodes(root) {
if (root === null) {
return 0;
}
let l = totalNodes(root.left);
let r = totalNodes(root.right);
return 1 + l + r;
}
function newNode(data) {
return new Node(data);
}
let root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.left = newNode(9);
root.right.right = newNode(8);
root.left.left.left = newNode(6);
root.left.left.right = newNode(7);
document.write(totalNodes(root));
</script>
|
Time Complexity: O(N) as in traversal all the nodes are visited
Reason:
- Recurrence Relation: T(N) = 2*T(N/2) + O(1)
- Solve via Master’s Theorem, you will get O(N) as Time.
Auxiliary Space: O(h) = O(log N) as height of CBT is LogN
Reason:
- Recursion Stack Space (which takes elements up to the height of the tree)
- As you will go left, left till the corner leaf node. All of these stay in the stack on top of one another.
Better Approach :
We know how to traverse the tree using recursion or using data structures like stack and queue. But the problem is these data structures consume O(n) space (Why O(n):- Because we need to traverse all the elements so they need to be required to be stored in specific data structures). Recursive functions use something called “the call stack” which consumes O(n) space. You can learn even more about time complexity by clicking here
So now the only option left with us that is to think of doing changes to the links. Let’s see how to accomplish this task in O(1) space (constant space).
Approach :
1)Make a pointer which points to current node
2)Continue steps above till the current node pointer is not null
3)If the left of the pointer is NULL , then increment count and move to right.
4)If left pointer is not null , make another temporary pointer to one left of current pointer and move towards right till
it's not null
Dry Run:
Let’s take an example and find the number of nodes
Example :
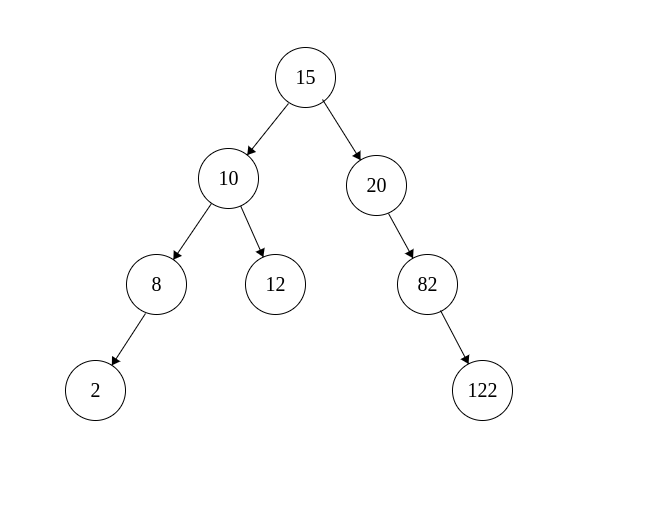
Tree
1) Lets take 2 variables , current = 15 and prev = NULL and count = 0 .
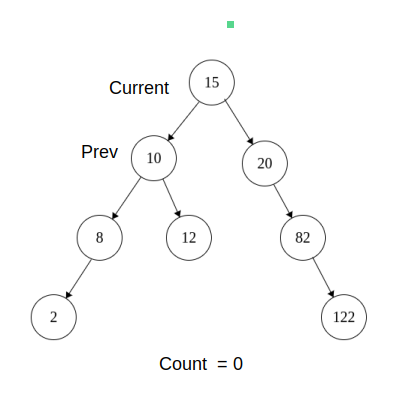
Tree
2) We should continue the following process until the current node is NULL
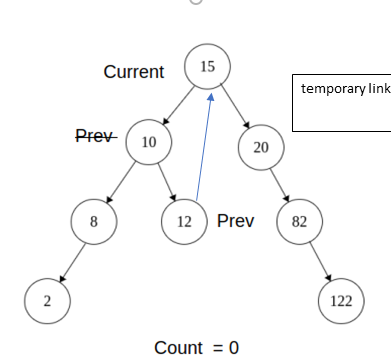
3) If Current -> left != NULL , prev = 10
Now iterate prev to right until prev -> right != NULL && prev -> right != current
so now prev = 12
Now prev -> right = NULL, therefore just make a temporary link to current i.e make a temporary right link from 12 to 15 , and move current to left
Current = 10
Tree
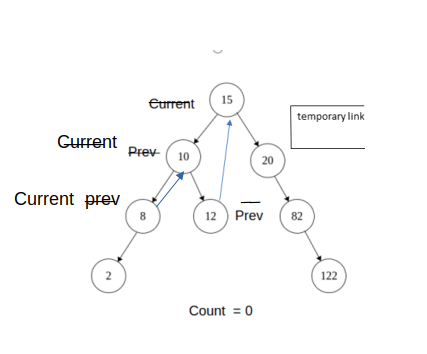
4) Again repeat step 3) , Now prev = 8 and its right is NULL, so again make a temporary right link from 8 to 10 and move current to left
Current = 8
Tree
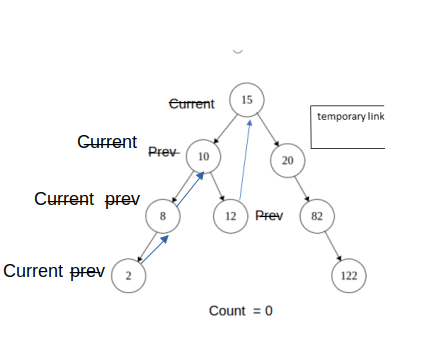
5)Again repeat step 3) , Now prev = 2 and its right is NULL, so again make a temporary right link from 2 to 8 and move current to left
Current = 2
Tree
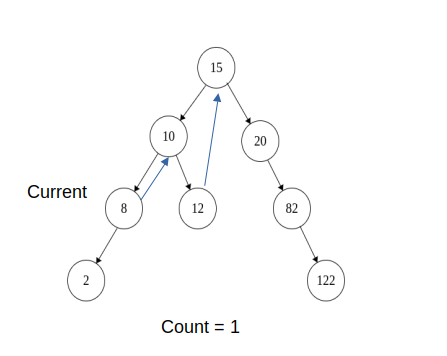
6)Now current -> left == NULL, So increment count and move current to its right
count = 1
current = 8 (We have a temporary pointer so we are able to go back)
Tree
7)Again repeat step 3) , Now prev = 2 and its right is NULL, now when we iterate in loop prev -> right != curr, we stop when prev -> right = NULL
i.e prev = 2 , so make prev -> right = NULL and increment the count,move current to current -> right
The temporary link from 2 -> 8 is removed
Current = 10
Count = 2
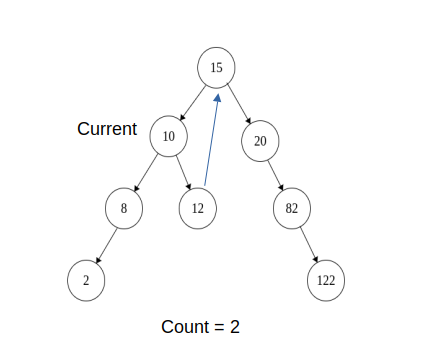
Tree
8)Again repeat step 3) , Now prev = 8 and its right is NULL, now when we iterate in loop prev -> right != curr, we stop when prev -> right = NULL
i.e prev = 8 , so make prev -> right = NULL and increment the count,move current to current -> right
The temporary link from 8 -> 10 is removed
Current = 12
Count = 3
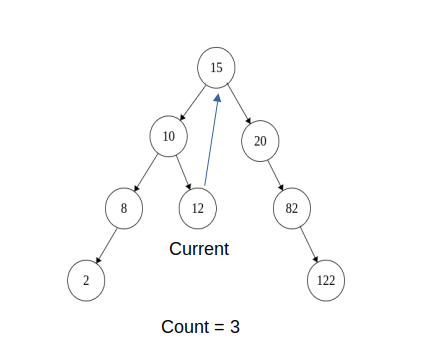
Tree
9)Now current -> left is NULL, increment count and moves current to current -> right
Current = 15
Count = 4
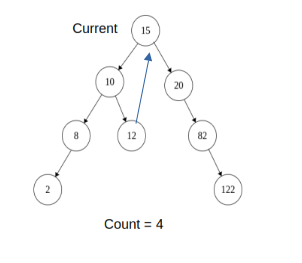
10)Again repeat step 3), Now prev = 10 and its right is NULL, now when we iterate in loop prev -> right != curr, we stop when prev -> right = NULL
i.e prev = 12 , so make prev -> right = NULL and increment the count,move current to current -> right
The temporary link from 12 -> 15 is removed
Current = 20
Count = 5
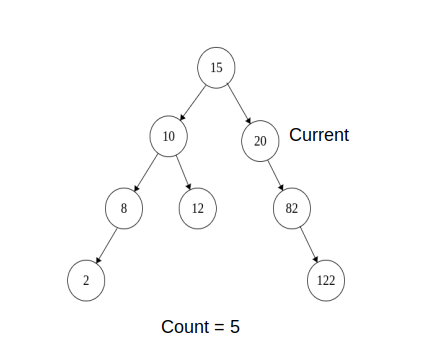
Tree
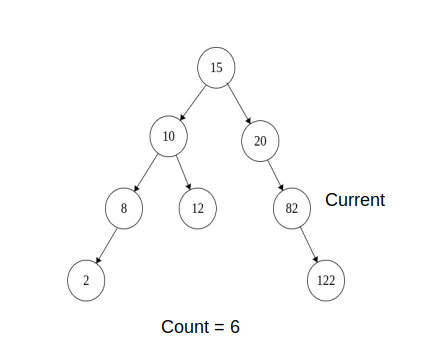
11)Now current -> left is NULL, increment count and moves current to current -> right
Current = 20
Count = 6
Tree
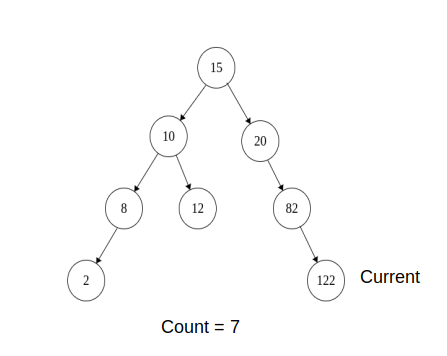
12)Now current -> left is NULL, increment count and moves current to current -> right
Current = 82
Count = 7
Tree
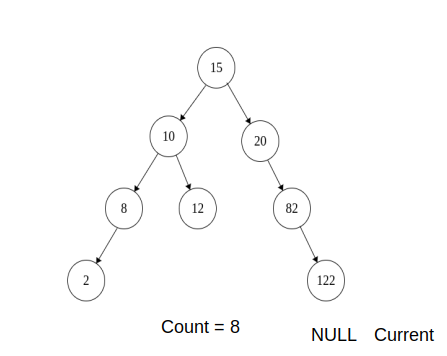
13)Now current -> left is NULL, increment count and moves current to current -> right
Current = 122
Count = 8
Tree
14)Now the current is NULL, so stop the loop .
In this way, we have found the count of nodes in a binary search tree in O(1) space.
C++
#include <iostream>
using namespace std;
struct tree {
int data;
tree* left;
tree* right;
};
typedef tree* Tree;
void initTree(Tree& tnode)
{
tnode = nullptr;
}
void insertIntoTree(Tree& tnode, int data)
{
Tree newnode = new tree;
newnode->left = nullptr;
newnode->right = nullptr;
newnode->data = data;
if (!tnode) {
tnode = newnode;
return;
}
Tree current = tnode, prev = nullptr;
while (current) {
prev = current;
if (current->data
== data)
return;
else if (current->data > data)
current
= current->left;
else
current
= current->right;
}
if (prev->data > data)
prev->left = newnode;
else
prev->right = newnode;
return;
}
int getCountOfNodes(Tree tnode)
{
int count = 0;
Tree curr = tnode;
while (curr != nullptr) {
if (curr->left
== nullptr) {
count++;
curr = curr->right;
}
else {
Tree prev
= curr->left;
while (prev->right && prev->right != curr)
prev
= prev->right;
if (prev->right
== nullptr) {
prev->right
= curr;
curr = curr->left;
}
else {
prev->right
= nullptr;
count++;
curr = curr->right;
}
}
}
return count;
}
int main()
{
Tree tree1;
initTree(tree1);
insertIntoTree(tree1, 15);
insertIntoTree(tree1, 10);
insertIntoTree(tree1, 20);
insertIntoTree(tree1,
8);
insertIntoTree(tree1, 12);
insertIntoTree(tree1, 82);
insertIntoTree(tree1, 122);
insertIntoTree(tree1, 2);
int count = getCountOfNodes(tree1);
cout << "Count of nodes in O(1) space : " << count
<< endl;
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
typedef struct tree {
int data;
struct tree* left;
struct tree* right;
} tree;
typedef tree* Tree;
void initTree(Tree* tnode)
{
*tnode = NULL;
}
void insertIntoTree(Tree* tnode, int data)
{
Tree newnode = (tree*)malloc(sizeof(tree));
newnode->left = NULL;
newnode->right = NULL;
newnode->data = data;
if (!*tnode) {
*tnode = newnode;
return;
}
Tree current = *tnode, prev = NULL;
while (current) {
prev = current;
if (current->data
== data)
return;
else if (current->data > data)
current
= current->left;
else
current
= current->right;
}
if (prev->data > data)
prev->left = newnode;
else
prev->right = newnode;
return;
}
int getCountOfNodes(Tree tnode)
{
int count = 0;
Tree curr = tnode;
while (curr != NULL) {
if (curr->left
== NULL) {
count++;
curr = curr->right;
}
else {
Tree prev
= curr->left;
while (prev->right && prev->right != curr)
prev = prev->right;
if (prev->right
== NULL) {
prev->right
= curr;
curr = curr->left;
}
else {
prev->right
= NULL;
count++;
curr = curr->right;
}
}
}
return count;
}
int main()
{
Tree tree1;
initTree(&tree1);
insertIntoTree(&tree1, 15);
insertIntoTree(&tree1, 10);
insertIntoTree(&tree1, 20);
insertIntoTree(&tree1,
8);
insertIntoTree(&tree1, 12);
insertIntoTree(&tree1, 82);
insertIntoTree(&tree1, 122);
insertIntoTree(&tree1, 2);
int count = getCountOfNodes(tree1);
printf("Count of nodes in O(1) space : %d \n", count);
return 0;
}
|
Java
class TreeNode {
int data;
TreeNode left;
TreeNode right;
public TreeNode(int data) {
this.data = data;
this.left = null;
this.right = null;
}
}
public class BinaryTree {
TreeNode root;
public BinaryTree() {
root = null;
}
public void insert(int data) {
root = insertRec(root, data);
}
private TreeNode insertRec(TreeNode root, int data) {
if (root == null) {
root = new TreeNode(data);
return root;
}
if (data < root.data) {
root.left = insertRec(root.left, data);
} else if (data > root.data) {
root.right = insertRec(root.right, data);
}
return root;
}
public int getCountOfNodes() {
return getCountOfNodesRec(root);
}
private int getCountOfNodesRec(TreeNode root) {
int count = 0;
TreeNode current = root;
while (current != null) {
if (current.left == null) {
count++;
current = current.right;
} else {
TreeNode prev = current.left;
while (prev.right != null && prev.right != current) {
prev = prev.right;
}
if (prev.right == null) {
prev.right = current;
current = current.left;
} else {
prev.right = null;
count++;
current = current.right;
}
}
}
return count;
}
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
tree.insert(15);
tree.insert(10);
tree.insert(20);
tree.insert(8);
tree.insert(12);
tree.insert(82);
tree.insert(122);
tree.insert(2);
int count = tree.getCountOfNodes();
System.out.println("Count of nodes in O(1) space: " + count);
}
}
|
Python
class TreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def initTree():
return None
def insertIntoTree(root, data):
if root is None:
return TreeNode(data)
current, prev = root, None
while current:
prev = current
if current.data == data:
return root
elif current.data > data:
current = current.left
else:
current = current.right
new_node = TreeNode(data)
if prev.data > data:
prev.left = new_node
else:
prev.right = new_node
return root
def getCountOfNodes(root):
count = 0
current = root
while current:
if current.left is None:
count += 1
current = current.right
else:
prev = current.left
while prev.right and prev.right != current:
prev = prev.right
if prev.right is None:
prev.right = current
current = current.left
else:
prev.right = None
count += 1
current = current.right
return count
if __name__ == "__main__":
root = initTree()
root = insertIntoTree(root, 15)
root = insertIntoTree(root, 10)
root = insertIntoTree(root, 20)
root = insertIntoTree(root, 8)
root = insertIntoTree(root, 12)
root = insertIntoTree(root, 82)
root = insertIntoTree(root, 122)
root = insertIntoTree(root, 2)
count = getCountOfNodes(root)
print("Count of nodes in O(1) space:", count)
|
C#
using System;
public class TreeNode
{
public int data;
public TreeNode left;
public TreeNode right;
}
public class BinarySearchTree
{
public TreeNode root;
public BinarySearchTree()
{
root = null;
}
public void Insert(int data)
{
TreeNode newNode = new TreeNode
{
data = data,
left = null,
right = null
};
if (root == null)
{
root = newNode;
return;
}
TreeNode current = root;
TreeNode prev = null;
while (current != null)
{
prev = current;
if (current.data == data)
{
return;
}
else if (current.data > data)
{
current = current.left;
}
else
{
current = current.right;
}
}
if (prev.data > data)
{
prev.left = newNode;
}
else
{
prev.right = newNode;
}
}
public int GetCountOfNodes()
{
int count = 0;
TreeNode current = root;
while (current != null)
{
if (current.left == null)
{
count++;
current = current.right;
}
else
{
TreeNode prev = current.left;
while (prev.right != null && prev.right != current)
{
prev = prev.right;
}
if (prev.right == null)
{
prev.right = current;
current = current.left;
}
else
{
prev.right = null;
count++;
current = current.right;
}
}
}
return count;
}
public static void Main()
{
BinarySearchTree tree = new BinarySearchTree();
tree.Insert(15);
tree.Insert(10);
tree.Insert(20);
tree.Insert(8);
tree.Insert(12);
tree.Insert(82);
tree.Insert(122);
tree.Insert(2);
int count = tree.GetCountOfNodes();
Console.WriteLine("Count of nodes in O(1) space: " + count);
}
}
|
Javascript
class TreeNode {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
class BinaryTree {
constructor() {
this.root = null;
}
insert(data) {
this.root = this.insertRec(this.root, data);
}
insertRec(root, data) {
if (root === null) {
root = new TreeNode(data);
return root;
}
if (data < root.data) {
root.left = this.insertRec(root.left, data);
} else if (data > root.data) {
root.right = this.insertRec(root.right, data);
}
return root;
}
getCountOfNodes() {
return this.getCountOfNodesRec(this.root);
}
getCountOfNodesRec(root) {
let count = 0;
let current = root;
while (current !== null) {
if (current.left === null) {
count++;
current = current.right;
} else {
let prev = current.left;
while (prev.right !== null && prev.right !== current) {
prev = prev.right;
}
if (prev.right === null) {
prev.right = current;
current = current.left;
} else {
prev.right = null;
count++;
current = current.right;
}
}
}
return count;
}
}
const tree = new BinaryTree();
tree.insert(15);
tree.insert(10);
tree.insert(20);
tree.insert(8);
tree.insert(12);
tree.insert(82);
tree.insert(122);
tree.insert(2);
const count = tree.getCountOfNodes();
console.log("Count of nodes in O(1) space: " + count);
|
Output
Count of nodes in O(1) space : 8
Time Complexity: O(n) ( We visit each node at most once, so the time complexity is an order of n i.e n)
Space complexity: O(1) (We just use some temporary pointer variables to make changes in links, no additional data structure or recursion is used)
Efficient Approach: The above approach can also be optimized by the fact that:
A complete binary tree can have at most (2h + 1 – 1) nodes in total where h is the height of the tree (This happens when all the levels are completely filled).
By this logic, in the first case, compare the left sub-tree height with the right sub-tree height. If they are equal it is a full tree, then the answer will be 2^height – 1. Otherwise, If they aren’t equal, recursively call for the left sub-tree and the right sub-tree to count the number of nodes. Follow the steps below to solve the problem:
- Define a function left_height(root) and find the left height of the given Tree by traversing in the root’s left direction and store it in a variable, say leftHeight.
- Define a function right_height(root) and find the right height of the given Tree by traversing in the root’s right direction and store it in a variable, say rightHeight.
- Find the left and the right height of the given Tree for the current root value and if it is equal then return the value of (2height – 1) as the resultant count of nodes.
- Otherwise, recursively call for the function for the left and right sub-trees and return the sum of them + 1 as the resultant count of nodes.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
class node {
public:
int data;
node* left;
node* right;
};
node* newNode(int data);
int left_height(node* node)
{
int ht = 0;
while (node) {
ht++;
node = node->left;
}
return ht;
}
int right_height(node* node)
{
int ht = 0;
while (node) {
ht++;
node = node->right;
}
return ht;
}
int TotalNodes(node* root)
{
if (root == NULL)
return 0;
int lh = left_height(root);
int rh = right_height(root);
if (lh == rh)
return (1 << lh) - 1;
return 1 + TotalNodes(root->left)
+ TotalNodes(root->right);
}
node* newNode(int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
int main()
{
node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(9);
root->right->right = newNode(8);
root->left->left->left = newNode(6);
root->left->left->right = newNode(7);
cout << TotalNodes(root);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
typedef struct node {
int data;
struct node* left;
struct node* right;
}node;
node* newNode(int data)
{
node * Node = (node *)malloc(sizeof(node));
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
int left_height(node* node)
{
int ht = 0;
while (node) {
ht++;
node = node->left;
}
return ht;
}
int right_height(node* node)
{
int ht = 0;
while (node) {
ht++;
node = node->right;
}
return ht;
}
int TotalNodes(node* root)
{
if (root == NULL)
return 0;
int lh = left_height(root);
int rh = right_height(root);
if (lh == rh)
return (1 << lh) - 1;
return 1 + TotalNodes(root->left) + TotalNodes(root->right);
}
int main()
{
node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(9);
root->right->right = newNode(8);
root->left->left->left = newNode(6);
root->left->left->right = newNode(7);
printf("%d",TotalNodes(root));
return 0;
}
|
Java
import java.util.*;
class GFG{
static class node {
int data;
node left;
node right;
};
static int left_height(node node)
{
int ht = 0;
while (node!=null) {
ht++;
node = node.left;
}
return ht;
}
static int right_height(node node)
{
int ht = 0;
while (node!=null) {
ht++;
node = node.right;
}
return ht;
}
static int TotalNodes(node root)
{
if (root == null)
return 0;
int lh = left_height(root);
int rh = right_height(root);
if (lh == rh)
return (1 << lh) - 1;
return 1 + TotalNodes(root.left)
+ TotalNodes(root.right);
}
static node newNode(int data)
{
node Node = new node();
Node.data = data;
Node.left = null;
Node.right = null;
return (Node);
}
public static void main(String[] args)
{
node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.left = newNode(9);
root.right.right = newNode(8);
root.left.left.left = newNode(6);
root.left.left.right = newNode(7);
System.out.print(TotalNodes(root));
}
}
|
Python3
class node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
def left_height(node):
ht = 0
while(node):
ht += 1
node = node.left
return ht
def right_height(node):
ht = 0
while(node):
ht += 1
node = node.right
return ht
def TotalNodes(root):
if(root == None):
return 0
lh = left_height(root)
rh = right_height(root)
if(lh == rh):
return (1 << lh) - 1
return 1 + TotalNodes(root.left) + TotalNodes(root.right)
root = node(1)
root.left = node(2)
root.right = node(3)
root.left.left = node(4)
root.left.right = node(5)
root.right.left = node(9)
root.right.right = node(8)
root.left.left.left = node(6)
root.left.left.right = node(7)
print(TotalNodes(root))
|
C#
using System;
public class GFG{
class node {
public int data;
public node left;
public node right;
};
static int left_height(node node)
{
int ht = 0;
while (node != null) {
ht++;
node = node.left;
}
return ht;
}
static int right_height(node node)
{
int ht = 0;
while (node != null) {
ht++;
node = node.right;
}
return ht;
}
static int TotalNodes(node root)
{
if (root == null)
return 0;
int lh = left_height(root);
int rh = right_height(root);
if (lh == rh)
return (1 << lh) - 1;
return 1 + TotalNodes(root.left)
+ TotalNodes(root.right);
}
static node newNode(int data)
{
node Node = new node();
Node.data = data;
Node.left = null;
Node.right = null;
return (Node);
}
public static void Main(String[] args)
{
node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.left = newNode(9);
root.right.right = newNode(8);
root.left.left.left = newNode(6);
root.left.left.right = newNode(7);
Console.Write(TotalNodes(root));
}
}
|
Javascript
<script>
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
};
function left_height(node) {
let ht = 0;
while (node) {
ht++;
node = node.left;
}
return ht;
}
function right_height(node) {
let ht = 0;
while (node) {
ht++;
node = node.right;
}
return ht;
}
function TotalNodes(root) {
if (root == null)
return 0;
let lh = left_height(root);
let rh = right_height(root);
if (lh == rh)
return (1 << lh) - 1;
return 1 + TotalNodes(root.left)
+ TotalNodes(root.right);
}
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(9);
root.right.right = new Node(8);
root.left.left.left = new Node(6);
root.left.left.right = new Node(7);
document.write(TotalNodes(root));
</script>
|
Time Complexity: O((log N)2)
- Calculating the height of a tree with x nodes takes (log x) time.
- Here, we are traversing through the height of the tree.
- For each node, height calculation takes logarithmic time.
- As the number of nodes is N, we are traversing log(N) nodes and calculating the height for each of them.
- So the total complexity is (log N * log N) = (log N)2.
Auxiliary Space: O(log N) because of Recursion Stack Space (which takes elements upto the maximum depth of a node in the tree)
Share your thoughts in the comments
Please Login to comment...