Print path from root to all nodes in a Complete Binary Tree

Given a number N which is the total number of nodes in a complete binary tree where nodes are number from 1 to N sequentially level-wise. The task is to write a program to print paths from root to all of the nodes in the Complete Binary Tree.
For N = 3, the tree will be: 

     1
  /     \
2        3 

For N = 7, the tree will be: 

       1
    /     \
   2        3 
 /   \    /  \ 
4    5    6   7

Examples:

Input : 7  
Output : 
1 
1 2 
1 2 4 
1 2 5 
1 3 
1 3 6 
1 3 7 

Input : 4 
Output :
1 
1 2 
1 2 4 
1 3 

Explanation:- Since, the given tree is a complete binary tree. For every node 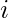we can calculate its left child as 2*i and right child as 2*i + 1.
The idea is to use a backtracking approach to print all paths. Maintain a vector to store paths, initially push the root node 1 to it, and before pushing the left and right children print the current path stored in it and then call the function for the left and right children as well. 
Below is the complete implementation of the above approach:

C++

// C++ program to print path from root to all
// nodes in a complete binary tree.

#include <iostream>
#include <vector>
using namespace std;

// Function to print path of all the nodes
// nth node represent as given node
// kth node represents as left and right node
void printPath(vector<int> res, int nThNode, int kThNode)
{
    // base condition
    // if kth node value is greater
    // then nth node then its means
    // kth node is not valid so
    // we not store it into the res
    // simply we just return
    if (kThNode > nThNode)
        return;

    // Storing node into res
    res.push_back(kThNode);

    // Print the path from root to node
    for (int i = 0; i < res.size(); i++)
        cout << res[i] << " ";
    cout << "\n";

    // store left path of a tree
    // So for left we will go node(kThNode*2)
    printPath(res, nThNode, kThNode * 2);

    // right path of a tree
    // and for right we will go node(kThNode*2+1)
    printPath(res, nThNode, kThNode * 2 + 1);
}

// Function to print path from root to all of the nodes
void printPathToCoverAllNodeUtil(int nThNode)
{
    // res is for store the path
    // from root to particulate node
    vector<int> res;

    // Print path from root to all node.
    // third argument 1 because of we have
    // to consider root node is 1
    printPath(res, nThNode, 1);
}

// Driver Code
int main()
{
    // Given Node
    int nThNode = 7;

    // Print path from root to all node.
    printPathToCoverAllNodeUtil(nThNode);

    return 0;
}

Java

// Java program to print path from root to all
// nodes in a complete binary tree.
import java.util.*;

class GFG
{

// Function to print path of all the nodes
// nth node represent as given node
// kth node represents as left and right node
static void printPath(Vector<Integer> res,
                    int nThNode, int kThNode)
{
    // base condition
    // if kth node value is greater
    // then nth node then its means
    // kth node is not valid so
    // we not store it into the res
    // simply we just return
    if (kThNode > nThNode)
        return;

    // Storing node into res
    res.add(kThNode);

    // Print the path from root to node
    for (int i = 0; i < res.size(); i++)
        System.out.print( res.get(i) + " ");
    System.out.print( "\n");

    // store left path of a tree
    // So for left we will go node(kThNode*2)
    printPath(res, nThNode, kThNode * 2);

    // right path of a tree
    // and for right we will go node(kThNode*2+1)
    printPath(res, nThNode, kThNode * 2 + 1);

    res.remove(res.size()-1);
}

// Function to print path from root to all of the nodes
static void printPathToCoverAllNodeUtil(int nThNode)
{
    // res is for store the path
    // from root to particulate node
    Vector<Integer> res=new Vector<Integer>();

    // Print path from root to all node.
    // third argument 1 because of we have
    // to consider root node is 1
    printPath(res, nThNode, 1);
}

// Driver Code
public static void main(String args[])
{
    // Given Node
    int nThNode = 7;

    // Print path from root to all node.
    printPathToCoverAllNodeUtil(nThNode);
}
}

// This code is contributed by Arnab Kundu

Python3

# Python3 program to print path from root
# to all nodes in a complete binary tree.

# Function to print path of all the nodes
# nth node represent as given node kth
# node represents as left and right node
def printPath(res, nThNode, kThNode):

    # base condition
    # if kth node value is greater
    # then nth node then its means
    # kth node is not valid so
    # we not store it into the res
    # simply we just return
    if kThNode > nThNode:
        return

    # Storing node into res
    res.append(kThNode)

    # Print the path from root to node
    for i in range(0, len(res)):
        print(res[i], end = " ")
    print()

    # store left path of a tree
    # So for left we will go node(kThNode*2)
    printPath(res[:], nThNode, kThNode * 2)

    # right path of a tree
    # and for right we will go node(kThNode*2+1)
    printPath(res[:], nThNode, kThNode * 2 + 1)

# Function to print path from root
# to all of the nodes
def printPathToCoverAllNodeUtil(nThNode):

    # res is for store the path
    # from root to particulate node
    res = []

    # Print path from root to all node.
    # third argument 1 because of we have
    # to consider root node is 1
    printPath(res, nThNode, 1)

# Driver Code
if __name__ == "__main__":

    # Given Node
    nThNode = 7

    # Print path from root to all node.
    printPathToCoverAllNodeUtil(nThNode)

# This code is contributed by Rituraj Jain

C#

// C# program to print path from root to all
// nodes in a complete binary tree.
using System;
using System.Collections.Generic;

class GFG
{

// Function to print path of all the nodes
// nth node represent as given node
// kth node represents as left and right node
static void printPath(List<int> res,
                    int nThNode, int kThNode)
{
    // base condition
    // if kth node value is greater
    // then nth node then its means
    // kth node is not valid so
    // we not store it into the res
    // simply we just return
    if (kThNode > nThNode)
        return;

    // Storing node into res
    res.Add(kThNode);

    // Print the path from root to node
    for (int i = 0; i < res.Count; i++)
        Console.Write( res[i] + " ");
    Console.Write( "\n");

    // store left path of a tree
    // So for left we will go node(kThNode*2)
    printPath(res, nThNode, kThNode * 2);

    // right path of a tree
    // and for right we will go node(kThNode*2+1)
    printPath(res, nThNode, kThNode * 2 + 1);

    res.RemoveAt(res.Count-1);
}

// Function to print path from root to all of the nodes
static void printPathToCoverAllNodeUtil(int nThNode)
{
    // res is for store the path
    // from root to particulate node
    List<int> res=new List<int>();

    // Print path from root to all node.
    // third argument 1 because of we have
    // to consider root node is 1
    printPath(res, nThNode, 1);
}

// Driver Code
public static void Main(String []args)
{
    // Given Node
    int nThNode = 7;

    // Print path from root to all node.
    printPathToCoverAllNodeUtil(nThNode);
}
}

// This code contributed by Rajput-Ji

PHP

<?php
// PHP program to print path from root to all
// nodes in a complete binary tree.

// Function to print path of all the nodes
// nth node represent as given node
// kth node represents as left and right node
function printPath($res, $nThNode, $kThNode)
{
    // base condition
    // if kth node value is greater
    // then nth node then its means
    // kth node is not valid so
    // we not store it into the res
    // simply we just return
    if ($kThNode > $nThNode)
        return;

    // Storing node into res
    array_push($res, $kThNode);

    // Print the path from root to node
    for ($i = 0; $i < count($res); $i++)
        echo $res[$i] . " ";
    echo "\n";

    // store left path of a tree
    // So for left we will go node(kThNode*2)
    printPath($res, $nThNode, $kThNode * 2);

    // right path of a tree
    // and for right we will go node(kThNode*2+1)
    printPath($res, $nThNode, $kThNode * 2 + 1);
}

// Function to print path
// from root to all of the nodes
function printPathToCoverAllNodeUtil($nThNode)
{
    // res is for store the path
    // from root to particulate node
    $res = array();

    // Print path from root to all node.
    // third argument 1 because of we have
    // to consider root node is 1
    printPath($res, $nThNode, 1);
}

// Driver Code

// Given Node
$nThNode = 7;

// Print path from root to all node.
printPathToCoverAllNodeUtil($nThNode);

// This code is contributed by mits
?>

Javascript

<script>

// JavaScript program to print path from root to all
// nodes in a complete binary tree.

// Function to print path of all the nodes
// nth node represent as given node
// kth node represents as left and right node
function printPath(res, nThNode, kThNode)
{
    // base condition
    // if kth node value is greater
    // then nth node then its means
    // kth node is not valid so
    // we not store it into the res
    // simply we just return
    if (kThNode > nThNode)
        return;

    // Storing node into res
    res.push(kThNode);

    // Print the path from root to node
    for (var i = 0; i < res.length; i++)
        document.write( res[i] + " ");
    document.write( "<br>");

    // store left path of a tree
    // So for left we will go node(kThNode*2)
    printPath(res, nThNode, kThNode * 2);

    // right path of a tree
    // and for right we will go node(kThNode*2+1)
    printPath(res, nThNode, kThNode * 2 + 1);

    res.pop()
}

// Function to print path from root to all of the nodes
function printPathToCoverAllNodeUtil( nThNode)
{
    // res is for store the path
    // from root to particulate node
    var res = [];

    // Print path from root to all node.
    // third argument 1 because of we have
    // to consider root node is 1
    printPath(res, nThNode, 1);
}

// Driver Code

// Given Node
var nThNode = 7;

// Print path from root to all node.
printPathToCoverAllNodeUtil(nThNode);


</script>

Output:

1 
1 2 
1 2 4 
1 2 5 
1 3 
1 3 6 
1 3 7

Time Complexity: O(N*H) where N is the number of nodes and H is the height of binary tree.
Auxiliary Space: O(H) where H is the height of binary tree.