Convert given Binary Tree to Symmetric Tree by adding minimum number of nodes

Given a Binary Tree, the task is to convert the given Binary Tree to the Symmetric Tree by adding the minimum number of nodes in the given Tree.

Examples:

Input:
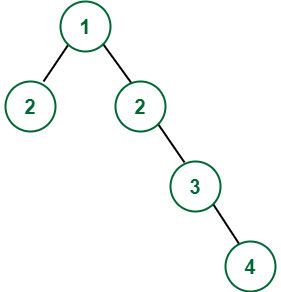
Output:
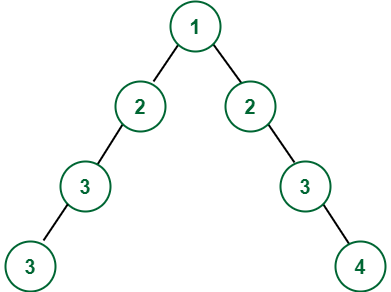
Input:
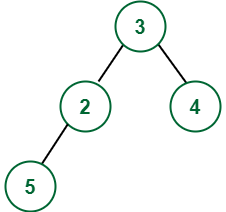
Output:

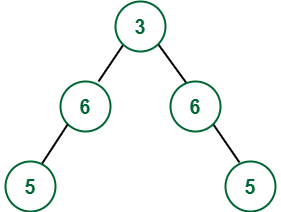
Approach: To solve this problem, follow the below steps:

Make a function buildSymmetricTree which will accept two parameters root1 and root2.
Here, root1 and root2, are the nodes that are at the symmetrical places of one another.
So initially, both root1 and root2 will contain the value of the root and in each recursive call:
- If root1 exists but root2 doesn’t then create a new node with the value same as root1 and place it in the position of root2.
- Follow the above step also for root1 if root2 exists but root1 doesn’t.
- If the value of root1 and root2 is not the same, then change the value of both nodes to the sum of them.
- Now, make the next two recursive calls for the symmetrical positions at (root1->left, root2->right) and (root1->right, root2->left).
The tree will become symmetrical after all recursive calls will be made.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Node
class Node {
public:
    int val;
    Node *left, *right;
    Node(int val)
    {
        this->val = val;
        left = right = NULL;
    }
};
 
// Function to convert the given tree
// into a symmetric
Node* buidSymmetricTree(Node* root1,
                         Node* root2)
{
    // Base Case
    if (root1 == NULL and root2 == NULL) {
        return NULL;
    }
 
    // If root1 == NULL & root2 != NULL
    if (root1 == NULL) {
 
        // Create new node for root2
        // and attaching it to tree
        Node* node = new Node(root2->val);
        root1 = node;
    }
 
    // If root2 == NULL and root1 != NULL
    if (root2 == NULL) {
 
        // Create new node for root1
        // and attaching it to tree
        Node* node = new Node(root1->val);
        root2 = node;
    }
 
    // If both nodes are different
    // then change both nodes values
    // to the sum of them
    if (root1->val != root2->val) {
        int temp = root1->val + root2->val;
        root1->val = temp;
        root2->val = temp;
    }
 
    // Recurring to the left
    root1->left
        = buidSymmetricTree(
            root1->left, root2->right);
 
    // Recurring to the right
    root1->right
        = buidSymmetricTree(
            root1->right, root2->left);
 
    // Return root pointer
    return root1;
}
 
// Function to perform the Inorder
// Traversal of the tree
void inorder(Node* root)
{
    // Base Case
    if (root == NULL)
        return;
 
    inorder(root->left);
    cout << root->val << " ";
    inorder(root->right);
}
 
// Driver Code
int main()
{
    Node* root = new Node(3);
    root->left = new Node(2);
    root->right = new Node(4);
    root->left->left = new Node(5);
 
    // Function to make the given
    // tree symmetric
    buidSymmetericTree(root, root);
 
    // Print the inorder traversal
    inorder(root);
 
    return 0;
}

Java

// Java program for the above approach
import java.util.*;
class GFG{
 
// Node
static class Node {
    int val;
    Node left, right;
    Node(int val)
    {
        this.val = val;
        left = right = null;
    }
};
 
// Function to convert the given tree
// into a symmetric
static Node buidSymmetricTree(Node root1,
                         Node root2)
{
    // Base Case
    if (root1 == null && root2 == null) {
        return null;
    }
 
    // If root1 == null & root2 != null
    if (root1 == null) {
 
        // Create new node for root2
        // and attaching it to tree
        Node node = new Node(root2.val);
        root1 = node;
    }
 
    // If root2 == null and root1 != null
    if (root2 == null) {
 
        // Create new node for root1
        // and attaching it to tree
        Node node = new Node(root1.val);
        root2 = node;
    }
 
    // If both nodes are different
    // then change both nodes values
    // to the sum of them
    if (root1.val != root2.val) {
        int temp = root1.val + root2.val;
        root1.val = temp;
        root2.val = temp;
    }
 
    // Recurring to the left
    root1.left
        = buidSymmetricTree(
            root1.left, root2.right);
 
    // Recurring to the right
    root1.right
        = buidSymmetricTree(
            root1.right, root2.left);
 
    // Return root pointer
    return root1;
}
 
// Function to perform the Inorder
// Traversal of the tree
static void inorder(Node root)
{
    // Base Case
    if (root == null)
        return;
 
    inorder(root.left);
    System.out.print(root.val+ " ");
    inorder(root.right);
}
 
// Driver Code
public static void main(String[] args)
{
    Node root = new Node(3);
    root.left = new Node(2);
    root.right = new Node(4);
    root.left.left = new Node(5);
 
    // Function to make the given
    // tree symmetric
    buidSymmetericTree(root, root);
 
    // Print the inorder traversal
    inorder(root);
}
}
 
// This code is contributed by umadevi9616

Python3

# Python Program to implement
# the above approach
 
# Node
class Node:
 
    def __init__(self, val):
        self.val = val
        self.left = self.right = None
     
 
 
# Function to convert the given tree
# into a symmetric
def buidSymmetricTree(root1, root2):
    # Base Case
    if (root1 == None and root2 == None):
        return None
     
 
    # If root1 == null & root2 != null
    if (root1 == None):
 
        # Create new node for root2
        # and attaching it to tree
        node = Node(root2.val)
        root1 = node
     
 
    # If root2 == null and root1 != null
    if (root2 == None):
 
        # Create new node for root1
        # and attaching it to tree
        node = Node(root1.val)
        root2 = node
     
 
    # If both nodes are different
    # then change both nodes values
    # to the sum of them
    if (root1.val != root2.val):
        temp = root1.val + root2.val
        root1.val = temp
        root2.val = temp
     
 
    # Recurring to the left
    root1.left = buidSymmetricTree( root1.left, root2.right)
 
    # Recurring to the right
    root1.right = buidSymmetricTree(root1.right, root2.left)
 
    # Return root pointer
    return root1
 
 
# Function to perform the Inorder
# Traversal of the tree
def inorder(root):
    # Base Case
    if (root == None):
      return
 
    inorder(root.left)
    print(root.val, end=" ")
    inorder(root.right)
 
 
# Driver Code
 
root = Node(3)
root.left = Node(2)
root.right = Node(4)
root.left.left = Node(5)
 
# Function to make the given
# tree symmetric
buidSymmetericTree(root, root)
 
# Print the inorder traversal
inorder(root)
 
# This code is contributed by gfgking.

C#

// C# program for the above approach
using System;
public class GFG {
 
    // Node
public    class Node {
    public    int val;
    public    Node left, right;
 
    public    Node(int val) {
            this.val = val;
            left = right = null;
        }
    };
 
    // Function to convert the given tree
    // into a symmetric
    static Node buidSymmetricTree(Node root1, Node root2)
    {
       
        // Base Case
        if (root1 == null && root2 == null) {
            return null;
        }
 
        // If root1 == null & root2 != null
        if (root1 == null) {
 
            // Create new node for root2
            // and attaching it to tree
            Node node = new Node(root2.val);
            root1 = node;
        }
 
        // If root2 == null and root1 != null
        if (root2 == null) {
 
            // Create new node for root1
            // and attaching it to tree
            Node node = new Node(root1.val);
            root2 = node;
        }
 
        // If both nodes are different
        // then change both nodes values
        // to the sum of them
        if (root1.val != root2.val) {
            int temp = root1.val + root2.val;
            root1.val = temp;
            root2.val = temp;
        }
 
        // Recurring to the left
        root1.left = buidSymmetricTree(root1.left, root2.right);
 
        // Recurring to the right
        root1.right = buidSymmetricTree(root1.right, root2.left);
 
        // Return root pointer
        return root1;
    }
 
    // Function to perform the Inorder
    // Traversal of the tree
    static void inorder(Node root)
    {
       
        // Base Case
        if (root == null)
            return;
 
        inorder(root.left);
        Console.Write(root.val + " ");
        inorder(root.right);
    }
 
    // Driver Code
    public static void Main(String[] args) {
        Node root = new Node(3);
        root.left = new Node(2);
        root.right = new Node(4);
        root.left.left = new Node(5);
 
        // Function to make the given
        // tree symmetric
        buidSymmetericTree(root, root);
 
        // Print the inorder traversal
        inorder(root);
    }
}
 
// This code is contributed by gauravrajput1

Javascript

<script>
        // JavaScript Program to implement
        // the above approach
 
 
        // Node
        class Node {
 
            constructor(val) {
                this.val = val;
                this.left = this.right = null;
            }
        };
 
        // Function to convert the given tree
        // into a symmetric
        function buidSymmetricTree(root1,
            root2) {
            // Base Case
            if (root1 == null && root2 == null) {
                return null;
            }
 
            // If root1 == null & root2 != null
            if (root1 == null) {
 
                // Create new node for root2
                // and attaching it to tree
                let node = new Node(root2.val);
                root1 = node;
            }
 
            // If root2 == null and root1 != null
            if (root2 == null) {
 
                // Create new node for root1
                // and attaching it to tree
                let node = new Node(root1.val);
                root2 = node;
            }
 
            // If both nodes are different
            // then change both nodes values
            // to the sum of them
            if (root1.val != root2.val) {
                let temp = root1.val + root2.val;
                root1.val = temp;
                root2.val = temp;
            }
 
            // Recurring to the left
            root1.left
                = buidSymmetricTree(
                    root1.left, root2.right);
 
            // Recurring to the right
            root1.right
                = buidSymmetricTree(
                    root1.right, root2.left);
 
            // Return root pointer
            return root1;
        }
 
        // Function to perform the Inorder
        // Traversal of the tree
        function inorder(root) {
            // Base Case
            if (root == null)
                return;
 
            inorder(root.left);
            document.write(root.val + " ");
            inorder(root.right);
        }
 
        // Driver Code
 
        let root = new Node(3);
        root.left = new Node(2);
        root.right = new Node(4);
        root.left.left = new Node(5);
 
        // Function to make the given
        // tree symmetric
        buidSymmetericTree(root, root);
 
        // Print the inorder traversal
        inorder(root);
 
// This code is contributed by Potta Lokesh
    </script>