Cosets in Mathematics
Last Updated :
07 Sep, 2020
Coset is subset of mathematical group consisting of all the products obtained by multiplying fixed element of group by each of elements of given subgroup, either on right or on left.mCosets are basic tool in study of groups
Suppose if
A is group, and
B is subgroup of
A, and is an element of
A, then
aB = {ab : b an element of B } is left coset of B in A,
The left coset of
B in
A is subset of
A of form
aB for some
a(element of
A). In
aB(left coset),
a is representative of coset.
and
Ba = {ba : b an element of B } is right coset of B in A.
The right coset of
B in
A is subset of
A of form
Ba for some
a(element of
A). In right coset
Ba, element
a is referred to as representative of coset.
The map
aB -> (aB)' = Ba' map defines bijection between left cosets and
B‘s right cosets, so total of left cosets is equivalent to total of right cosets. The common value is called index of
B in
A.
Left cosets and right cosets are always the same in case of abelian groupings. Notation used switches to
a+B or
B+a if group operation is written additively.
Definition using Equivalence Classes :
Some authors define the left cosets of
B in
A as equivalence classes given by
x ~ y under equivalence relationship on
A if and only if
x'y subset of
B is given. Relation can also be described by
x ~ y if and only if
xb = y is described in
B for certain
b. It can be seen that given relation is simply an equivalence relationship and that two concepts are identical. Consequently, two left
B-in-
A cosets are either equivalent or disjoint. So, every element of
A belongs to single left coset and so left cosets form partition of
A. Similar claims for right cosets are also valid.
Double Cosets :
If
A is group,
B and
C are subgroups of
A, then in
A double coset of
B and
C are sets of
BaC = {
bac:
b an element of
B,
c an element of
B }. These are left cosets of
C and right cosets of
B, respectively, if
B=1 and
C=1.
Notation :
Suppose
A is group and
B and
C.are subgroups of
A.
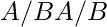 denotes
denotes  set of left cosetsof
set of left cosetsof B in A.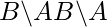 denotes
denotes 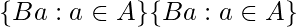 set of right cosets of
set of right cosets of B in A.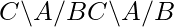 denotes
denotes 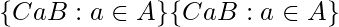 set of double cosets of
set of double cosets of B and C in A.
Applications :
- In computational group theory, cosets are essential.
- Cosets play key role in the theorem for Lagrange.
- The Thistlethwaite’s algorithm used to solve Rubik’s Cube is highly based on cosets.
- linear error-correction in obtained decoded data is done using cosets.
- They are used to construct Vitali sets, kind of non-measurable package.
Share your thoughts in the comments
Please Login to comment...