Construct a tree from Inorder and Level order traversals | Set 1
Last Updated :
26 Jul, 2022
Given inorder and level-order traversals of a Binary Tree, construct the Binary Tree. Following is an example to illustrate the problem.
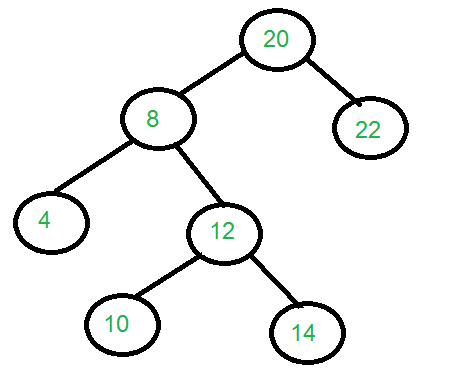
Input: Two arrays that represent Inorder
and level order traversals of a
Binary Tree
in[] = {4, 8, 10, 12, 14, 20, 22};
level[] = {20, 8, 22, 4, 12, 10, 14};
Output: Construct the tree represented
by the two arrays.
For the above two arrays, the
constructed tree is shown in
the diagram on right side
The following post can be considered as a prerequisite for this.
Construct Tree from given Inorder and Preorder traversals
Let us consider the above example.
- in[] = {4, 8, 10, 12, 14, 20, 22};
- level[] = {20, 8, 22, 4, 12, 10, 14};
In a Levelorder sequence, the first element is the root of the tree. So we know ’20’ is root for given sequences. By searching ’20’ in Inorder sequence, we can find out all elements on left side of ‘20’ are in left subtree and elements on right are in right subtree. So we know below structure now.
20
/ \
/ \
{4,8,10,12,14} {22}
Let us call {4,8,10,12,14} as left subarray in Inorder traversal and {22} as right subarray in Inorder traversal.
In level order traversal, keys of left and right subtrees are not consecutive. So we extract all nodes from level order traversal which are in left subarray of Inorder traversal. To construct the left subtree of root, we recur for the extracted elements from level order traversal and left subarray of inorder traversal. In the above example, we recur for the following two arrays.
// Recur for following arrays to construct the left subtree
In[] = {4, 8, 10, 12, 14}
level[] = {8, 4, 12, 10, 14}
Similarly, we recur for the following two arrays and construct the right subtree.
// Recur for following arrays to construct the right subtree
In[] = {22}
level[] = {22}
Following is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
struct Node *left, *right;
};
int search(int arr[], int strt, int end, int value)
{
for (int i = strt; i <= end; i++)
if (arr[i] == value)
return i;
return -1;
}
int* extrackKeys(int in[], int level[], int m, int n)
{
int *newlevel = new int[m], j = 0;
for (int i = 0; i < n; i++)
if (search(in, 0, m - 1, level[i]) != -1)
newlevel[j] = level[i], j++;
return newlevel;
}
Node* newNode(int key)
{
Node* node = new Node;
node->key = key;
node->left = node->right = NULL;
return (node);
}
Node* buildTree(int in[], int level[], int inStrt,
int inEnd, int n)
{
if (inStrt > inEnd)
return NULL;
Node* root = newNode(level[0]);
if (inStrt == inEnd)
return root;
int inIndex = search(in, inStrt, inEnd, root->key);
int* llevel = extrackKeys(in, level, inIndex, n);
int* rlevel
= extrackKeys(in + inIndex + 1, level, n - 1, n);
root->left = buildTree(in, llevel, inStrt, inIndex - 1,
inIndex - inStrt);
root->right = buildTree(in, rlevel, inIndex + 1, inEnd,
inEnd - inIndex);
delete[] llevel;
delete[] rlevel;
return root;
}
void printInorder(Node* node)
{
if (node == NULL)
return;
printInorder(node->left);
cout << node->key << " ";
printInorder(node->right);
}
int main()
{
int in[] = { 4, 8, 10, 12, 14, 20, 22 };
int level[] = { 20, 8, 22, 4, 12, 10, 14 };
int n = sizeof(in) / sizeof(in[0]);
Node* root = buildTree(in, level, 0, n - 1, n);
cout << "Inorder traversal of the constructed tree is "
"\n";
printInorder(root);
return 0;
}
|
Java
class Node {
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
public void setLeft(Node left) { this.left = left; }
public void setRight(Node right) { this.right = right; }
}
class Tree {
Node root;
Node buildTree(int in[], int level[])
{
Node startnode = null;
return constructTree(startnode, level, in, 0,
in.length - 1);
}
Node constructTree(Node startNode, int[] levelOrder,
int[] inOrder, int inStart,
int inEnd)
{
if (inStart > inEnd)
return null;
if (inStart == inEnd)
return new Node(inOrder[inStart]);
boolean found = false;
int index = 0;
for (int i = 0; i < levelOrder.length - 1; i++) {
int data = levelOrder[i];
for (int j = inStart; j < inEnd; j++) {
if (data == inOrder[j]) {
startNode = new Node(data);
index = j;
found = true;
break;
}
}
if (found == true)
break;
}
startNode.setLeft(
constructTree(startNode, levelOrder, inOrder,
inStart, index - 1));
startNode.setRight(
constructTree(startNode, levelOrder, inOrder,
index + 1, inEnd));
return startNode;
}
void printInorder(Node node)
{
if (node == null)
return;
printInorder(node.left);
System.out.print(node.data + " ");
printInorder(node.right);
}
public static void main(String args[])
{
Tree tree = new Tree();
int in[] = new int[] { 4, 8, 10, 12, 14, 20, 22 };
int level[]
= new int[] { 20, 8, 22, 4, 12, 10, 14 };
int n = in.length;
Node node = tree.buildTree(in, level);
System.out.print(
"Inorder traversal of the constructed tree is ");
tree.printInorder(node);
}
}
|
Python3
class Node:
def __init__(self, key):
self.data = key
self.left = None
self.right = None
def buildTree(level, ino):
if ino:
for i in range(0, len(level)):
if level[i] in ino:
node = Node(level[i])
io_index = ino.index(level[i])
break
node.left = buildTree(level, ino[0:io_index])
node.right = buildTree(level, ino[io_index + 1:len(ino)])
return node
else:
return None
def printInorder(node):
if node is None:
return
printInorder(node.left)
print(node.data, end=" ")
printInorder(node.right)
levelorder = [20, 8, 22, 4, 12, 10, 14]
inorder = [4, 8, 10, 12, 14, 20, 22]
ino_len = len(inorder)
root = buildTree(levelorder, inorder)
print("Inorder traversal of the constructed tree is")
printInorder(root)
|
C#
using System;
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
public virtual Node Left
{
set { this.left = value; }
}
public virtual Node Right
{
set { this.right = value; }
}
}
class GFG {
public Node root;
public virtual Node buildTree(int[] arr, int[] level)
{
Node startnode = null;
return constructTree(startnode, level, arr, 0,
arr.Length - 1);
}
public virtual Node
constructTree(Node startNode, int[] levelOrder,
int[] inOrder, int inStart, int inEnd)
{
if (inStart > inEnd) {
return null;
}
if (inStart == inEnd) {
return new Node(inOrder[inStart]);
}
bool found = false;
int index = 0;
for (int i = 0; i < levelOrder.Length - 1; i++) {
int data = levelOrder[i];
for (int j = inStart; j < inEnd; j++) {
if (data == inOrder[j]) {
startNode = new Node(data);
index = j;
found = true;
break;
}
}
if (found == true) {
break;
}
}
startNode.Left
= constructTree(startNode, levelOrder, inOrder,
inStart, index - 1);
startNode.Right
= constructTree(startNode, levelOrder, inOrder,
index + 1, inEnd);
return startNode;
}
public virtual void printInorder(Node node)
{
if (node == null) {
return;
}
printInorder(node.left);
Console.Write(node.data + " ");
printInorder(node.right);
}
public static void Main(string[] args)
{
GFG tree = new GFG();
int[] arr = new int[] { 4, 8, 10, 12, 14, 20, 22 };
int[] level
= new int[] { 20, 8, 22, 4, 12, 10, 14 };
int n = arr.Length;
Node node = tree.buildTree(arr, level);
Console.Write("Inorder traversal of the "
+ "constructed tree is "
+ "\n");
tree.printInorder(node);
}
}
|
Javascript
<script>
class Node{
constructor(key){
this.data = key
this.left = null
this.right = null
}
}
function buildTree(level, ino)
{
if(ino.length > 0)
{
let io_index;
let node;
for (let i = 0; i < level.length; i++)
{
if(ino.indexOf(level[i]) !== -1)
{
node = new Node(level[i])
io_index = ino.indexOf(level[i]);
break
}
}
node.left = buildTree(level, ino.slice(0,io_index))
node.right = buildTree(level, ino.slice(io_index+1,ino.length))
return node
}
else return null;
}
function printInorder(node){
if(node === null)
return
printInorder(node.left)
document.write(node.data," ")
printInorder(node.right)
}
let levelorder = [20, 8, 22, 4, 12, 10, 14];
let inorder = [4, 8, 10, 12, 14, 20, 22];
root = buildTree(levelorder, inorder);
document.write("Inorder traversal of the constructed tree is","</br>");
printInorder(root);
</script>
|
Output
Inorder traversal of the constructed tree is
4 8 10 12 14 20 20
An upper bound on time complexity of above method is O(n3). In the main recursive function, extractNodes() is called which takes O(n2) time.
The code can be optimized in many ways and there may be better solutions.
Time Complexity: O(n^3)
Space Complexity: O(n) where n is the number of nodes.
Construct a tree from Inorder and Level order traversals | Set 2
Share your thoughts in the comments
Please Login to comment...