Clustering-Based approaches for outlier detection in data mining
Last Updated :
10 Sep, 2021
Clustering Analysis is the process of dividing a set of data objects into subsets. Each subset is a cluster such that objects are similar to each other. The set of clusters obtained from clustering analysis can be referred to as Clustering. For example: Segregating customers in a Retail market as a frequent customer, new customer.
Basic approaches in Clustering:
Partition Methods:
Used to find mutually exclusive spherical clusters. It is based on remote clusters. It uses iterative movement technology to improve partitioning. To represent the center of the cluster, we can use the mean or center point. This is very effective for small and medium data sets.
Hierarchical Methods:
Creates hierarchical decomposition of the specified data record of the data object. They can be based on distance or density and continuity. They are divided into cohesion method and division method. If so, this is an outlier.
Density-Based Methods:
This method is a density-based approach for finding arbitrarily shaped clusters. The general idea of the density-based method is to continue growing a given cluster as long as the density exceeds some threshold. They mainly consider exclusive clusters only not the fizzy clusters. They can be extended from full space to sub-space clustering.
Grid-Based Methods:
Here we quantize the object into a finite grid number of cells forming a grid structure. All the operations are performed on the grid structure only. The main advantage of this method is the processing time which is much faster and independent of the number of objects.
Cluster-Based Approaches for detecting Outliers:
Clustering-based outlier detection methods assume that the normal data objects belong to large and dense clusters, whereas outliers belong to small or sparse clusters, or do not belong to any clusters. Clustering-based approaches detect outliers by extracting the relationship between Objects and Cluster. An object is an outlier if
- Does the object belong to any cluster? If not, then it is identified as an outlier.
- Is there a large distance between the object and the cluster to which it is closest? If yes, it is an outlier.
- Is the object part of a small or sparse cluster? If yes, then all the objects in that cluster are outliers.
Checking an outlier:
This K-Means makes use of a ratio 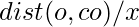
where,
co is the closest center to object o and
dist(o, co) is the distance between o and co
x is the average distance between co and o
Note that each of the procedures we’ve visible up to now detects individual objects items as outliers due to the fact they evaluate items separately in opposition to clusters withinside the information set. However, in a huge information set, a few outliers can be comparable and shape a small cluster. The procedures mentioned up to now can be deceived via way of means of such outliers.
To conquer this problem, the 3rd method to cluster-primarily based totally outlier detection identifies small or sparse clusters and pronounces the items in the one’s clusters to be outliers as well. An instance of this method is the FindCBLOF set of rules, which matches as follows.
1. Find clusters in an information set, and type them in step with reducing the length. The set of rules assumes that the maximum of the information factors aren’t outliers. It makes use of a parameter α (0 ≤ α ≤ 1) to differentiate huge from small clusters. Any cluster that incorporates at the least a percent α (e.g., α = 90%) of the information set is taken into consideration as a “huge cluster.” The final clusters are noted as “small clusters.”
2. To every information factor, assign a cluster-primarily based totally nearby outlier factor (CBLOF). For a factor belonging to a huge cluster, its CBLOF is made from the cluster’s length and the similarity among the factor and the cluster. For a factor belonging to a small cluster, its CBLOF is calculated because it the made from the dimensions of the small cluster and the similarity among the factor and the nearest huge cluster. CBLOF defines the similarity between a factor and a cluster in a statistical manner that represents the opportunity that the factor belongs to the cluster. The large the value, the extra comparable the factor and the cluster are. The CBLOF rating can locate outlier factors that might be some distance from any clusters. In addition, small clusters which might be some distance from any huge cluster are taken into consideration to encompass outliers. The factors with the bottom CBLOF rankings are suspected outliers. To detect outliers in small clusters we go with finding the cluster-based local outlier factor. To find CBLOF we should follow below steps:
- Find the clusters and sort them in decreasing order.
- To each cluster, points add a local outlier factor.
- If object p belongs to a larger part of the cluster, CBLOF = product of the size of the cluster and similarity between point and cluster.
- If object p belongs to a smaller one, CBLOF = product of the size of the cluster and similarity between point and the closest larger cluster.
Clustering-primarily based totally procedures can also additionally incur excessive computational charges in the event that they must discover clusters earlier than detecting outliers. Several strategies had been advanced for stepped forward efficiency. For instance, fixed-width clustering is a linear-time method this is utilized in a few outlier detection methods. The concept is easy but efficient. A factor is assigned to a cluster if the middle of the cluster is inside a predefined distance threshold from the factor. If a factor can not be assigned to any current cluster, the new cluster is created.
Strength and Weakness for cluster-based outlier detection:
Advantages: The cluster-based outlier detection method has the following advantages. First, they can detect outliers without labeling the data, that is, they are out of control. You deal with multiple types of data. You can think of a cluster as a collection of data. Once the cluster is obtained, the cluster-based method only needs to compare the object with the cluster to determine whether the object is an outlier. This process is usually fast because the number of clusters is usually small in comparison. In the total number of objects.
Disadvantages: The weakness of clustering outlier detection is its effectiveness, which largely depends on the clustering method used. These methods cannot be optimized for outlier detection. Clustering techniques for large data sets are usually expensive, which may be a bottleneck.
Share your thoughts in the comments
Please Login to comment...