Outlier Detection in High-Dimensional Data in Data Mining
Last Updated :
05 Dec, 2022
An outlier is a data object that deviates significantly from the rest of the data objects and behaves in a different manner. An outlier is an object that deviates significantly from the rest of the objects. They can be caused by measurement or execution errors. The analysis of outlier data is referred to as outlier analysis or outlier mining.
Outlier Detection in High-Dimensional Data:
We might need to find outliers in high-dimensional data for some applications. Effective outlier detection faces enormous obstacles as a result of the dimensionality curse. The distance between objects may become heavily dominated by noise as the dimension increases. This means that the distance and similarity between two points in a high-dimensional space might not accurately represent their actual relationship. As a result, traditional outlier detection techniques become less effective as dimensionality rises. These techniques primarily use proximity or density to identify outliers.
They ought to be able to identify outliers as well as explain what the outliers mean. A high-dimensional data set contains a lot of features (or dimensions), so identifying outliers without explaining why they are outliers is not very helpful. The interpretation of outliers may be based on various factors, such as the particular subspaces in which the outliers are manifested or a determination of the “outlier-ness” of the objects. Such an interpretation can assist users in comprehending the potential significance and meaning of the outliers. The techniques should work with sparsity in high-dimensional spaces. As the dimensionality increases, noise becomes more and more dominant in the distance between objects. Data in high-dimensional spaces are therefore frequently scarce. Outliers should be properly modeled, for instance, by being adaptable to the subspaces representing the outliers and capturing the local behavior of data. Because the distance between two objects monotonically increases with dimensionality, using a fixed-distance threshold against all subspaces to find outliers is not good. The quantity of subspaces grows exponentially with dimensionality. It is not scalable to conduct an exhaustive combinatorial exploration of the search space, which contains all conceivable subspaces.
Outlier detection methods for high-dimensional data can be divided into three main approaches. These include extending conventional outlier detection, finding outliers in subspaces, and modeling high-dimensional outliers.
Extending Conventional Outlier Detection:
One method expands on traditional outlier detection techniques for high-dimensional data. It makes use of the common proximity-based outlier models. However, it employs alternative metrics or creates subspaces and looks for outliers there to compensate for the degradation of proximity measures in high-dimensional spaces. An illustration of this strategy is the HilOut algorithm. HilOut detects outliers based on distance, but instead of using the absolute distance, it uses the ranks of distance. HilOut specifically finds the k-nearest neighbors of each object, o, denoted by nn1(o),:::,nnk(o), where k is an application-dependent parameter. The definition of an object’s weight is
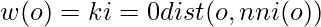
The weights of each object are listed in descending order. Outliers are output as the top-l objects in weight, where l is a further user-specified parameter.
When the database is large and the dimensionality is high, it is expensive to compute the k-nearest neighbors for each object. HilOut uses space-filling curves to achieve an approximation algorithm that is scalable in both running time and space with respect to database size and dimensionality to address the scalability issue.
Outlier detection techniques may be added to or used in place of general feature selection and extraction methods to reduce dimensionality. A lower-dimensional space can be extracted, for instance, using principal components analysis (PCA). On such dimensions, normal objects are probably close to one another and outliers frequently deviate from the majority, so heuristically, the principal components with low variance are preferred.
Finding Outliers in Subspaces:
Searching for outliers in different subspaces is another method for outlier detection in high-dimensional data. The fact that the subspace can be used to interpret why and to what extent an object is an outlier when it is discovered to be one in a much lower dimensional subspace gives it a distinct advantage. Due to the overwhelming number of dimensions, this insight is extremely beneficial in applications with high-dimensional data.
![Rendered by QuickLaTeX.com S(C) = [ n(C) - f k n ] / [ √f k (1-f k )n]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eb84b45c60f3a5269f751ef197d6e5f8_l3.png)
If S.C < 0, then C has fewer objects than anticipated. The less-dense C is, and the more likely it is that the objects in C are outliers in the subspace, the smaller the value of S.C (i.e., the more negative). We can use normal distribution tables to determine the probabilistic significance level for an object that deviates significantly from the average for an a priori assumption of the data following a uniform distribution by assuming S.C. follows a normal distribution. The assumption of uniform distribution is generally untrue. The sparsity coefficient, however, continues to offer a perceptible indicator of a region’s “outlier-ness.”
Modeling High-Dimensional Outliers:
An alternative method for finding outliers in high-dimensional data tries to directly create new models for high-dimensional outliers. These models typically do not use proximity measures but rather new heuristics to find outliers that do not degrade in high-dimensional data.
It is worth noting that the angles formed by a point in the center of a cluster vary greatly. The angle variation is smaller for a point near the edge of a cluster. The angle variable is significantly smaller for an outlier point. This observation implies that the variance of angles for a point can be used to determine whether a point is an outlier.
We can model outliers by combining angles and distance. Mathematically, we use the distance-weighted angle variance as the outlier score for each point o. In other words, given a set of points, D, for a point, o ∈ D, the angle-based outlier factor (ABOF) is defined as
![Rendered by QuickLaTeX.com ABOF(o) = VARx, y∈ D, x≠o ,y≠o [ox,oy] / dist(o,x)2 dist(o,y)2 ,](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ba250f6a5e42394cc63a9f68f59a0e9c_l3.png)
where [,] represents the scalar product operator and dist(,) represents a norm distance Clearly, the smaller the ABOF, the farther a point is from clusters and the smaller the variance of a point’s angles. The ABOD computes the ABOF for each point in the data set and returns a list of the points in ascending ABOF order. The time complexity of computing the exact ABOF for every point in a database is O(n3), where n is the number of points in the database. Clearly, this algorithm does not scale well for large data sets. To speed up the computation, approximation methods have been developed. The angle-based outlier detection concept has been generalised to work with any data type.
Conclusion:
Based on the information presented above, we conclude that outlier detection methods for high-dimensional data can be classified into three categories. Extending conventional outlier detection, finding outliers in subspaces, and modeling high-dimensional outliers are some of these. Finding appropriate data models, the dependence of outlier detection systems on the application involved, distinguishing outliers from noise, and providing justification for identifying outliers as such are all challenges in outlier detection.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...