Class 8 RD Sharma Solutions – Chapter 3 Squares and Square Roots – Exercise 3.7 | Set 2
Last Updated :
06 Apr, 2021
Question 11) 9998.0001
Solution:

Hence, the square root of 9998.0001 is 99.99.
Question 12) 0.00038809
Solution:

Hence, the square root of 84.8241 is 9.21.
Question 13) What is that fraction which when multiplied by itself gives 227.798629?
Solution:
We have to find the square root of the given number :

Hence, the fraction, which when multiplied by itself, gives 227.798649 is 15.093.
Question 14) The area of square playground is 256.6404 square meters. Find the length of one side of the playground.
Solution:
The length of one side of the playground is the square root of its area

So, the length of one side of the playground is 16.02 meters.
Question 15) What is the fraction which when multiplied by itself gives 0.00053361?
Solution:
We have to find the square root of the given number :

Hence, the fraction, which when multiplied by itself, gives 0.00053361 is 0.0231.
Question 16) Simplify:
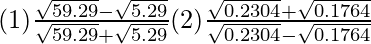
Solution:
1) First, finding the square roots of 5.29 and 59.29


On putting the values on their respective positions, we have (7.7 – 2.3) / (7.7 + 2.3) = 5.4/10 = 0.54.
Hence, the answer is 0.54.
2) First, finding the square roots of 0.2304 and 0.1764


On putting the values on their respective positions, we have (0.44 + 0.42) / (0.44 – 0.42) = 0.9/0.06 = 15.
Hence, the answer is 15.
Question 17) Evaluate √50625 and hence find the value of √506.25 + √5.0625
Solution:

Next, we calculate √506.25 and √5.0625
√506.25 = (√50625)/(√100) = 225/10 = 22.5
√5.0625 = (√50625)(√10000) = 225/100 = 2.25
√506.25 + √5.0625 = 22.5 + 2.25 = 24.75.
Question 18) Find the value of √103.0225 and hence find the value of:
1) √10302.25 2) √1.030225
Solution:
First, finding the square root of 103.0225

Hence, the square root of 103.0225 is 10.15
Now, we can solve the following questions as shown below:
1) √10302.25 = (√103.0225)×(√100) = 10.15×10 = 101.5
2) √1.030225 = (√103.0225)/(√100) = 10.15/10 = 1.015
Share your thoughts in the comments
Please Login to comment...