Class 8 RD Sharma Solutions – Chapter 3 Squares and Square Roots – Exercise 3.3 | Set 2

Chapter 3 Squares and Square Roots – Exercise 3.3 | Set 1

Question 4. Find the squares of the following numbers:

(i) 425

Solution:

425 = 420 + 5 = (42 x 10) + 5

Here, n = 42

=> n(n + 1) = 42(42 + 1) = 42 x 43 = 1806

=> 425² = 180625

(ii) 575

Solution:

575 = 570 + 5 = (57 x 10) + 5

Here, n = 57

=> n(n + 1) = 57(57 + 1) = 57 x 58 = 3306

=> 575² = 330625

(iii) 405

Solution:

405 = 400 + 5 = (40 x 10) + 5

Here, n = 40

=> n(n + 1) = 40(40 + 1) = 1640

=> 405² = 164025

(iv) 205

Solution:

205 = 200 + 5 = (20 x 10) + 5

Here, n = 20

=> n(n + 1) = 20(20 + 1) = 420

=> 205² = 42025

(v) 95

Solution:

95 = 90 + 5 = (9 x 10) + 5

Here, n = 9

=> n(n + 1) = 9(9 + 1) = 90

=> 95² = 9025

(vi) 745

Solution:

745 = 740 + 5 = (74 x 10) + 5

Here, n = 74

=> n(n + 1) = 74(74 + 1) = 5550

=> 745² = 555025

(vii) 512

Solution:

512² = (250 + 12)1000 + (12)² 

= (262)1000 + 144

= 262000 + 144

= 262144

Hence, 512² = 262144

(viii) 995

Solution:

995 = 990 + 5 = (99 x 10) + 5

Here, n = 99

=>n(n + 1) = 99(99 + 1) = 9900

995² = 990025

Question 5. Find the square of the following numbers using the formula: (a + b)² = a² + 2ab + b²

(i) 405 

Solution:

405 = 400 + 5 

Here, a = 400, b = 5

Using the identity, (a + b)² = a² + 2ab + b²

405² = 400² + (2 x 400 x 5) + 5²

= 160000 + 4000 + 25

= 164025

Thus, 405² = 164025

(ii) 510

Solution:

510 = 500 + 10

Here, a = 500, b = 10 

Using the identity, (a + b)² = a² + 2ab + b²

510² = 500² + (2 x 500 x 10) + 10²

= 250000 + 10000 + 100

= 260100

Thus, 510² = 260100

(iii) 1001

Solution:

1001 = 1000 + 1

Here, a = 1000, b = 1

Using the identity, (a + b)² = a² + 2ab + b²

1001² = 1000² + (2 x 1000 x 1) + 1²

= 1000000 + 2000 + 1

= 1002001

Thus, 1001² = 1002001 

(iv) 209

Solution:

209 = 200 + 9

Here, a = 200, b = 9

Using the identity, (a + b)² = a² + 2ab + b²

209² = 200² + (2 x 200 x 9) + 9²

= 40000 + 3600 + 81

= 43681

Thus, 209² = 43681

(v) 605

Solution:

605 = 600 + 5

Here, a = 600, b = 5

Using the identity, (a + b)² = a² + 2ab + b²

605² = 600² + (2 x 600 x 5) + 5²

= 360000 + 6000 + 25

= 366025

Thus, 605² = 366025

Question 6. Find the square of the following numbers using the formula: (a – b)² = a² – 2ab + b²

(i) 395

Solution:

395 = 400 – 5

Here, a = 400, b = 5

Using the identity, (a – b)² = a² – 2ab + b²

395² = (400 – 5)² = 400² – (2 x 400 x 5) + 5²

= 160000 – 4000 + 25

= 156025

Thus, 395² = 156025

(ii) 995

Solution:

995 = 1000 – 5

Here, a = 1000, b = 5

Using the identity, (a – b)² = a² – 2ab + b²

995² = (1000 – 5)² = 1000² – (2 x 1000 x 5) + 5²

= 1000000 – 10000 + 25

= 990025

Thus, 995² = 990025

(iii) 495

Solution:

495 = 500 – 5

Here, a = 500, b = 5

Using the identity, (a – b)² = a² – 2ab + b²

495² = (500 – 5)² = 500² – (2 x 500 x 5) + 5²

= 250000 – 5000 + 25

= 245025

Thus, 495² = 245025

(iv) 498

Solution:

498 = 500 – 2

Here, a = 500, b = 2

Using the identity, (a – b)² = a² – 2ab + b²

498² = (500 – 2)² = 500² – (2 x 500 x 2) + 2²

= 250000 – 2000 + 4

= 248004

Thus, 498² = 248004

(v) 99

Solution:

99 = 100 – 1

Here, a = 100, b = 1

99² = (100 – 1)² = 100² – (2 x 100 x 1) + 1²

= 10000 – 200 + 1

= 9801

Using the identity, (a – b)² = a² – 2ab + b²

Thus, 99² = 9801

(vi) 999

Solution:

999 = 1000 – 1

Here, a = 1000, b = 1

Using the identity, (a – b)² = a² – 2ab + b²

999² = (1000 – 1)² = 1000² – (2 x 1000 x 1) + 1²

= 1000000 – 2000 + 1

= 998001 

Thus, 999² = 998001

(vii) 599

Solution:

599 = 600 – 1

Here, a = 600, b = 1

Using the identity, (a – b)² = a² – 2ab + b²

599² = (600 – 1)² = 600² – (2 x 600 x 1) + 1²

= 360000 – 1200 + 1

= 358801

Thus, 599² = 358801

Question 7. Find the squares of the following numbers by the visual method:

(i) 52

Solution:

52 = 50 + 2

Here, a = 50, b = 2

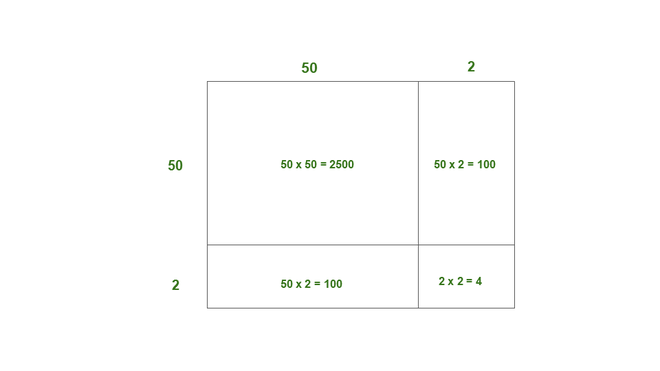
Thus, the area of square of side 52 = 2500 + 100 + 100 + 4

= 2704 

Thus, 52² = 2704

(ii) 95

Solution:

95 = 90 + 5

Here, a = 90, b = 5

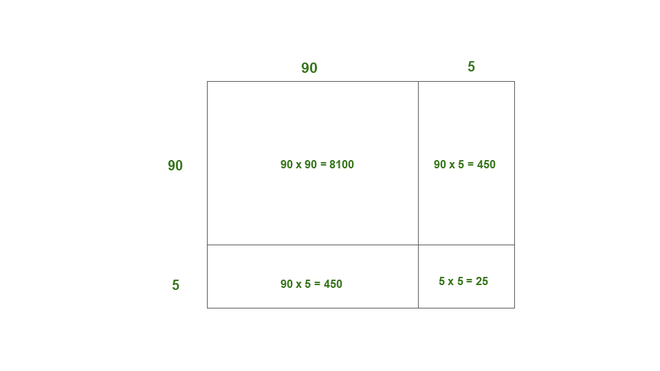
Thus, the area of square of side of 95 = 8100 + 450 + 450 + 25

= 9025

Thus, 95² = 9025

(iii) 505

Solution:

505 = 500 + 5

Here, a = 500, b = 5

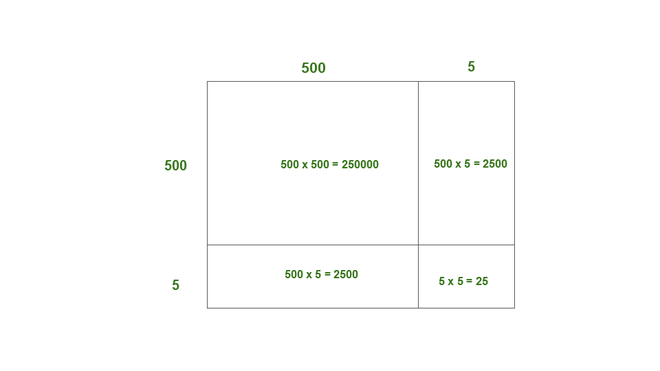
Thus, the area of square of side 505 = 250000 + 2500 + 2500 + 25

= 255025

Thus, 505² = 255025

(iv) 702

Solution:

702 = 700 + 2

Here, a = 700, b = 2

Thus, the area of square of side 702 = 490000 + 1400 + 1400 + 4

= 492804

Thus, 702² = 492804

(v) 99

Solution:

99 = 90 + 9

Here, a = 90, b = 9.

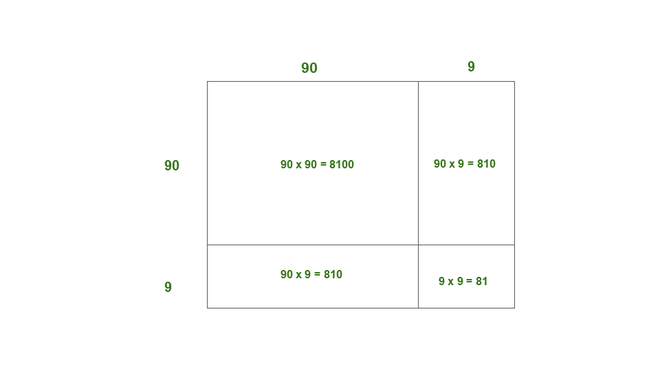
Thus, the area of square of side of 99 = 8100 + 810 + 810 + 81

= 9801 

Thus, 99² = 9801