Class 8 RD Sharma Solutions – Chapter 3 Squares and Square Roots – Exercise 3.3 | Set 2
Last Updated :
06 Apr, 2021
Question 4. Find the squares of the following numbers:
(i) 425
Solution:
425 = 420 + 5 = (42 x 10) + 5
Here, n = 42
=> n(n + 1) = 42(42 + 1) = 42 x 43 = 1806
=> 4252 = 180625
(ii) 575
Solution:
575 = 570 + 5 = (57 x 10) + 5
Here, n = 57
=> n(n + 1) = 57(57 + 1) = 57 x 58 = 3306
=> 5752 = 330625
(iii) 405
Solution:
405 = 400 + 5 = (40 x 10) + 5
Here, n = 40
=> n(n + 1) = 40(40 + 1) = 1640
=> 4052 = 164025
(iv) 205
Solution:
205 = 200 + 5 = (20 x 10) + 5
Here, n = 20
=> n(n + 1) = 20(20 + 1) = 420
=> 2052 = 42025
(v) 95
Solution:
95 = 90 + 5 = (9 x 10) + 5
Here, n = 9
=> n(n + 1) = 9(9 + 1) = 90
=> 952 = 9025
(vi) 745
Solution:
745 = 740 + 5 = (74 x 10) + 5
Here, n = 74
=> n(n + 1) = 74(74 + 1) = 5550
=> 7452 = 555025
(vii) 512
Solution:
512² = (250 + 12)1000 + (12)²
= (262)1000 + 144
= 262000 + 144
= 262144
Hence, 5122 = 262144
(viii) 995
Solution:
995 = 990 + 5 = (99 x 10) + 5
Here, n = 99
=>n(n + 1) = 99(99 + 1) = 9900
9952 = 990025
Question 5. Find the square of the following numbers using the formula: (a + b)2 = a2 + 2ab + b2
(i) 405
Solution:
405 = 400 + 5
Here, a = 400, b = 5
Using the identity, (a + b)2 = a2 + 2ab + b2
4052 = 4002 + (2 x 400 x 5) + 52
= 160000 + 4000 + 25
= 164025
Thus, 4052 = 164025
(ii) 510
Solution:
510 = 500 + 10
Here, a = 500, b = 10
Using the identity, (a + b)2 = a2 + 2ab + b2
5102 = 5002 + (2 x 500 x 10) + 102
= 250000 + 10000 + 100
= 260100
Thus, 5102 = 260100
(iii) 1001
Solution:
1001 = 1000 + 1
Here, a = 1000, b = 1
Using the identity, (a + b)2 = a2 + 2ab + b2
10012 = 10002 + (2 x 1000 x 1) + 12
= 1000000 + 2000 + 1
= 1002001
Thus, 10012 = 1002001
(iv) 209
Solution:
209 = 200 + 9
Here, a = 200, b = 9
Using the identity, (a + b)2 = a2 + 2ab + b2
2092 = 2002 + (2 x 200 x 9) + 92
= 40000 + 3600 + 81
= 43681
Thus, 2092 = 43681
(v) 605
Solution:
605 = 600 + 5
Here, a = 600, b = 5
Using the identity, (a + b)2 = a2 + 2ab + b2
6052 = 6002 + (2 x 600 x 5) + 52
= 360000 + 6000 + 25
= 366025
Thus, 6052 = 366025
Question 6. Find the square of the following numbers using the formula: (a – b)² = a² – 2ab + b²
(i) 395
Solution:
395 = 400 – 5
Here, a = 400, b = 5
Using the identity, (a – b)2 = a2 – 2ab + b2
3952 = (400 – 5)2 = 4002 – (2 x 400 x 5) + 52
= 160000 – 4000 + 25
= 156025
Thus, 3952 = 156025
(ii) 995
Solution:
995 = 1000 – 5
Here, a = 1000, b = 5
Using the identity, (a – b)2 = a2 – 2ab + b2
9952 = (1000 – 5)2 = 10002 – (2 x 1000 x 5) + 52
= 1000000 – 10000 + 25
= 990025
Thus, 9952 = 990025
(iii) 495
Solution:
495 = 500 – 5
Here, a = 500, b = 5
Using the identity, (a – b)2 = a2 – 2ab + b2
4952 = (500 – 5)2 = 5002 – (2 x 500 x 5) + 52
= 250000 – 5000 + 25
= 245025
Thus, 4952 = 245025
(iv) 498
Solution:
498 = 500 – 2
Here, a = 500, b = 2
Using the identity, (a – b)2 = a2 – 2ab + b2
4982 = (500 – 2)2 = 5002 – (2 x 500 x 2) + 22
= 250000 – 2000 + 4
= 248004
Thus, 4982 = 248004
(v) 99
Solution:
99 = 100 – 1
Here, a = 100, b = 1
992 = (100 – 1)2 = 1002 – (2 x 100 x 1) + 12
= 10000 – 200 + 1
= 9801
Using the identity, (a – b)2 = a2 – 2ab + b2
Thus, 992 = 9801
(vi) 999
Solution:
999 = 1000 – 1
Here, a = 1000, b = 1
Using the identity, (a – b)2 = a2 – 2ab + b2
9992 = (1000 – 1)2 = 10002 – (2 x 1000 x 1) + 12
= 1000000 – 2000 + 1
= 998001
Thus, 9992 = 998001
(vii) 599
Solution:
599 = 600 – 1
Here, a = 600, b = 1
Using the identity, (a – b)2 = a2 – 2ab + b2
5992 = (600 – 1)2 = 6002 – (2 x 600 x 1) + 12
= 360000 – 1200 + 1
= 358801
Thus, 5992 = 358801
Question 7. Find the squares of the following numbers by the visual method:
(i) 52
Solution:
52 = 50 + 2
Here, a = 50, b = 2
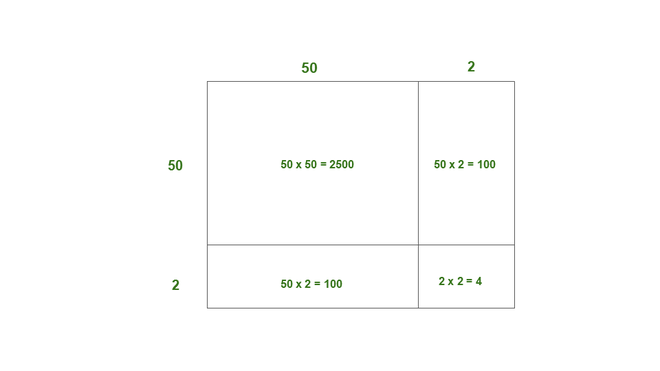
Thus, the area of square of side 52 = 2500 + 100 + 100 + 4
= 2704
Thus, 522 = 2704
(ii) 95
Solution:
95 = 90 + 5
Here, a = 90, b = 5
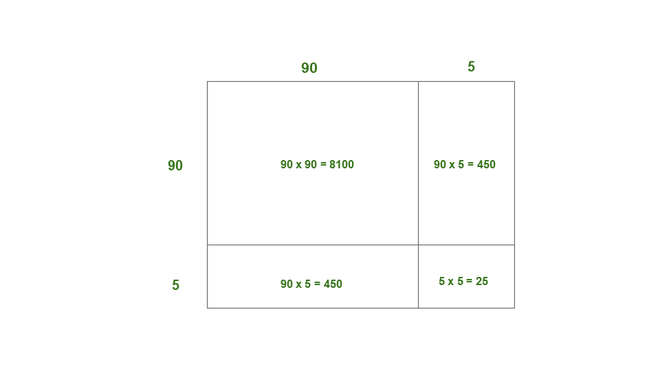
Thus, the area of square of side of 95 = 8100 + 450 + 450 + 25
= 9025
Thus, 952 = 9025
(iii) 505
Solution:
505 = 500 + 5
Here, a = 500, b = 5
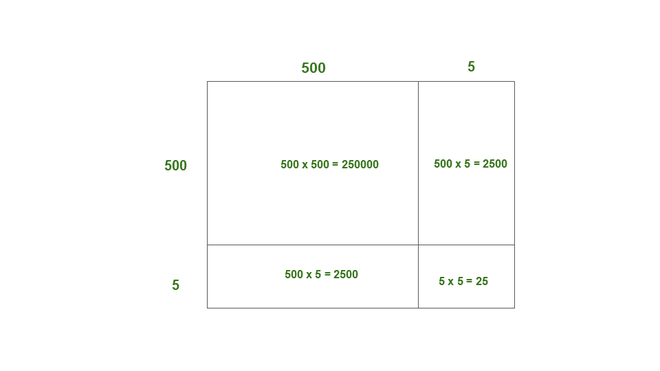
Thus, the area of square of side 505 = 250000 + 2500 + 2500 + 25
= 255025
Thus, 5052 = 255025
(iv) 702
Solution:
702 = 700 + 2
Here, a = 700, b = 2

Thus, the area of square of side 702 = 490000 + 1400 + 1400 + 4
= 492804
Thus, 7022 = 492804
(v) 99
Solution:
99 = 90 + 9
Here, a = 90, b = 9.
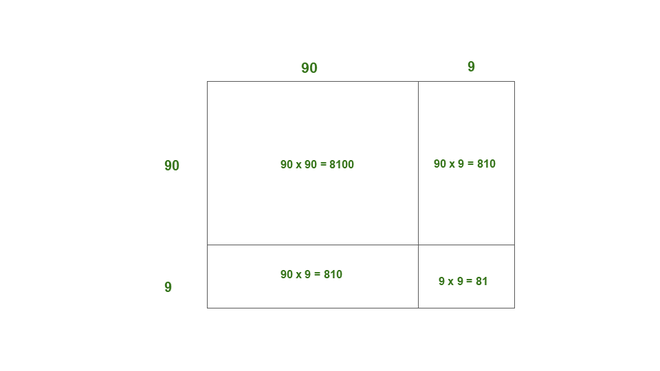
Thus, the area of square of side of 99 = 8100 + 810 + 810 + 81
= 9801
Thus, 992 = 9801
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...