Class 8 RD Sharma Solutions – Chapter 14 Compound Interest – Exercise 14.4 | Set 1
Last Updated :
08 Apr, 2021
Question 1. The present population of a town is 28000. If it increases at the rate of 5% per annum, what will be its population after 2 years?
Solution:
We have,
Present population of town is = 28000
Rate of increase in population is = 5% per annum
Number of years = 2
By using the formula,
A = P (1 + 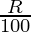 )n
)n
Substituting the values, we have
Population of town after 2 years = 28000 (1 + 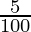 )2
)2
= 28000 (1.05)2
= 30870
Therefore,
Population of town after 2 years will be 30870.
Question 2. The population of a city is 125000. If the annual birth rate and death rate are 5.5% and 3.5% respectively, calculate the population of city after 3 years.
Solution:
We have,
Population of city (P) = 125000
Annual birth rate R1= 5.5 %
Annual death rate R2 = 3.5 %
Annual increasing rate R = (R1 – R2) = 5.5 – 3.5 = 2 %
Number of years = 3
By using the formula,
A = P (1 + 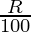 )n
)n
Substituting the values, we have
So, population after two years is = 125000 (1 + 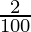 )3
)3
= 125000 (1.02)3
= 132651
Therefore,
Population after 3 years will be 132651.
Question 3. The present population of a town is 25000. It grows at 4%, 5% and 8% during first year, second year and third year respectively. Find its population after 3 years.
Solution:
We have,
Present population is = 25000
First year growth R1 = 4%
Second year growth R2 = 5%
Third year growth R3 = 8%
Number of years = 3
By using the formula,
A = P (1 + 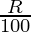 )n
)n
Substituting the values, we have
So, population after three years = P (1 + 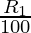 ) (1 +
) (1 + 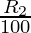 ) (1 +
) (1 + 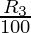 )
)
= 25000(1 + 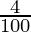 ) (1 +
) (1 + 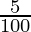 ) (1 +
) (1 + 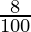 0)
0)
= 25000 (1.04) (1.05) (1.08)
= 29484
Therefore,
Population after 3 years will be 29484.
Question 4. Three years ago, the population of a town was 50000. If the annual increase during three successive years be at the rate of 4%, 5% and 3% respectively, find the present population.
Solution:
We have,
Three years ago population of town was = 50000
Annual increasing in 3 years = 4%,5%, 3% respectively
So, let present population be = x
By using the formula,
A = P (1 + 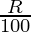 )n
)n
Substituting the values, we have
x = 50000 (1 + 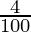 ) (1 +
) (1 + 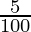 ) (1 +
) (1 + 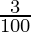 )
)
= 50000 (1.04) (1.05) (1.03)
= 56238
Therefore,
Present population of the town is 56238.
Question 5. There is a continuous growth in population of a village at the rate of 5% per annum. If its present population is 9261, what it was 3 years ago?
Solution:
We have,
Present population of town is = 9261
Continuous growth of population is = 5%
So, let population three years ago be = x
By using the formula,
A = P (1 + 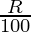 )n
)n
Substituting the values, we have
9261 = x (1 + 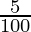 ) (1 +
) (1 + 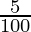 ) (1 +
) (1 + 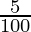 )
)
9261 = x (1.05) (1.05) (1.05)
= 8000
Therefore,
Present population of the town is 8000.
Question 6. In a factory the production of scooters rose to 46305 from 40000 in 3 years. Find the annual rate of growth of the production of scooters.
Solution:
We have,
Initial production of scooters is = 40000
Final production of scooters is = 46305
Time = 3 years
Let annual growth rate be = R%
By using the formula,
A = P (1 + 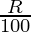 )n
)n
Substituting the values, we have
46305 = 40000 (1 + 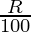 ) (1 +
) (1 + 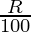 ) (1 +
) (1 + 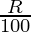 )
)
46305 = 40000 (1 + 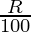 )3
)3
(1 + 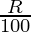 )3 = 46305/40000
)3 = 46305/40000
= 9261/8000
= (21/20)3
1 + 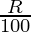 = 21/20
= 21/20
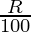 = 21/20 – 1
= 21/20 – 1
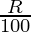 = (21-20)/20
= (21-20)/20
= 1/20
R = 100/20
= 5
Therefore,
Annual rate of growth of the production of scooters is 5%.
Question 7. The annual rate of growth in population of a certain city is 8%. If its present population is 196830, what it was 3 years ago?
Solution:
We have,
Annual growth rate of population of city is = 8%
Present population of city is = 196830
Let population of city 3 years ago be = x
By using the formula,
A = P (1 + 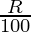 )n
)n
Substituting the values, we have
196830 = x (1 + 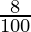 ) (1 +
) (1 + 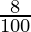 ) (1 +
) (1 + 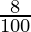 )
)
196830 = x (27/25) (27/25) (27/25)
196830 = x (1.08) (1.08) (1.08)
196830 = 1.259712x
x = 196830/1.259712
= 156250
Therefore,
Population 3 years ago was 156250.
Question 8. The population of a town increases at the rate of 50 per thousand. Its population after 2 years will be 22050. Find its present population.
Solution:
We have,
Growth rate of population of town is = 50/1000×100 = 5%
Population after 2 years is = 22050
So, let present population of town be = x
By using the formula,
A = P (1 + 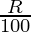 )n
)n
Substituting the values, we have
22050 = x (1 + 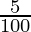 ) (1 +
) (1 + 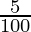 )
)
22050 = x (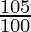 ) (
) (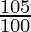 )
)
22050 = x (1.05) (1.05)
22050 = 1.1025x
x = 22050/1.1025
= 20000
Therefore,
Present population of the town is 20000.
Question 9. The count of bacteria in a culture grows by 10% in the first hour, decreases by 8% in the second hour and again increases by 12% in the third hour. If the count of bacteria in the sample is 13125000, what will be the count of bacteria after 3 hours?
Solution:
Given details are,
Count of bacteria in sample is = 13125000
The increase and decrease of growth rates are = 10%, -8%, 12%
So, let the count of bacteria after 3 hours be = x
By using the formula,
A = P (1 + 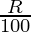 )n
)n
Substituting the values, we have
x = 13125000 (1 + 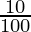 ) (1 –
) (1 – 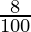 ) (1 +
) (1 + 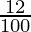 )
)
x = 13125000 (110/100) (92/100) (112/100)
x = 13125000 (1.1) (0.92) (1.12)
= 14876400
Therefore,
Count of bacteria after three hours will be 14876400.
Question 10. The population of a certain city was 72000 on the last day of the year 1998. During next year it increased by 7% but due to an epidemic it decreased by 10% in the following year. What was its population at the end of the year 2000?
Solution:
We have,
Population of city on last day of year 1998 = 72000
Increasing rate (R) in 1999 = 7%
Decreasing rate (R) in 2000 = 10 %
By using the formula,
A = P (1 + 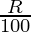 )n
)n
Substituting the values, we have
x = 72000 (1 + 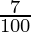 ) (1 –
) (1 – 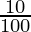 )
)
= 72000 (107/100) (90/100)
= 72000 (1.07) (0.9)
= 69336
Therefore,
Population at the end of the year 2000 will be 69336.
Share your thoughts in the comments
Please Login to comment...