Class 8 RD Sharma Solutions – Chapter 14 Compound Interest – Exercise 14.3 | Set 2
Last Updated :
08 Apr, 2021
Question 15. Find the rate percent per annum, if Rs. 2000 amount to Rs. 2315.25 in a year and a half, interest being compounded six monthly.
Solution:
We have,
Principal = Rs 2000
Amount = Rs 2315.25
Time = 1 ½ years = 3/2 years
Let rate be = R % per annum
By using the formula,
A = P (1 +  )n
)n
Substituting the values, we have
2315.25 = 2000 (1 +  )3/2
)3/2
(1 +  )3/2 = 2315.25/2000
)3/2 = 2315.25/2000
(1 +  )3/2 = (1.1576)
)3/2 = (1.1576)
(1 +  ) = 1.1025
) = 1.1025
 = 1.1025 – 1
= 1.1025 – 1
= 0.1025 × 100
= 10.25
Therefore,
Required Rate is 10.25% per annum.
Question 16. Find the rate at which a sum of money will double itself in 3 years, if the interest is compounded annually.
Solution:
We have,
Time = 3 years
Let rate be = R %
Also principal be = P
So, amount becomes = 2P
By using the formula,
A = P (1 +  )n
)n
Substituting the values, we have
2P = P (1 +  )3
)3
(1 +  )3 = 2
)3 = 2
(1 +  ) = 21/3
) = 21/3
1 +  = 1.2599
= 1.2599
 = 1.2599-1
= 1.2599-1
= 0.2599
R = 0.2599 × 100
= 25.99
Therefore,
Required Rate is 25.99% per annum.
Question 17. Find the rate at which a sum of money will become four times the original amount in 2 years, if the interest is compounded half-yearly
Solution:
We have,
Time = 2 years = 2×2 = 4 half years
Let rate = R % per annum = R/2% half years
Let principal be = P
So, Amount becomes = 4P
By using the formula,
A = P (1 +  )n
)n
Substituting the values, we have
4P = P (1 + 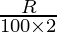 )4
)4
(1 + 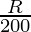 )4 = 4
)4 = 4
(1 + 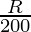 ) = 41/4
) = 41/4
1 + 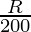 = 1.4142
= 1.4142
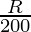 = 1.4142-1
= 1.4142-1
= 0.4142
R = 0.4142 × 200
= 82.84%
Therefore,
Required Rate is 82.84% per annum.
Question 18. A certain sum amounts to Rs. 5832 in 2 years at 8% compounded interest. Find the sum.
Solution:
We have,
Amount = Rs 5832
Time = 2 years
Rate = 8%
Let principal be = P
By using the formula,
A = P (1 +  )n
)n
Substituting the values, we have
5832 = P (1 + 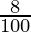 )2
)2
5832 = P (1.1664)
P = 5832/1.1664
= 5000
Therefore,
Required sum is Rs 5000.
Question 19. The difference between the compound interest and simple interest on a certain sum for 2 years at 7.5% per annum is Rs. 360. Find the sum.
Solution:
We have,
Time = 2 years
Rate = 7.5 % per annum
Let principal = Rs P
Compound Interest (CI) – Simple Interest (SI) = Rs 360
C.I – S.I = Rs 360
By using the formula,
P [(1 +  )n – 1] – (PTR)/100 = 360
)n – 1] – (PTR)/100 = 360
Substituting the values, we have
P [(1 + 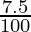 )2 – 1] – (P(2)(7.5))/100 = 360
)2 – 1] – (P(2)(7.5))/100 = 360
P[249/1600] – (3P)/20 = 360
249/1600P – 3/20P = 360
(249P-240P)/1600 = 360
9P = 360 × 1600
P = 576000/9
= 64000
Therefore,
The sum is Rs 64000.
Question 20. The difference in simple interest and compound interest on a certain sum of money at 623 % per annum for 3 years in Rs. 46. Determine the sum.
Solution:
We have,
Time = 3 years
Rate = 6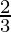 % per annum = 20/3%
% per annum = 20/3%
Let principal = Rs P
Compound Interest (CI) – Simple Interest (SI) = Rs 46
C.I – S.I = Rs 46
By using the formula,
P [(1 +  )n – 1] – (PTR)/100 = 46
)n – 1] – (PTR)/100 = 46
Substituting the values, we have
P [(1 + 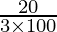 )3 – 1] – (P(3)(20/3))/100 = 46
)3 – 1] – (P(3)(20/3))/100 = 46
P[(1 + 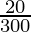 )3 – 1] – P/5 = 46
)3 – 1] – P/5 = 46
P[721/3375] – P/5 = 46
721/3375P – 1/5P = 46
(721P-675P)/3375 = 46
46P = 46 × 3375
46P = 46 × 3375/46
= 3375
Therefore,
The sum is Rs 3375.
Question 21. Ishita invested a sum of Rs. 12000 at 5% per annum compound interest. She received an amount of Rs. 13230 after n years. Find the value of n.
Solution:
We have,
Principal = Rs 12000
Amount = Rs 13230
Rate = 5% per annum
Let time = T years
By using the formula,
A = P (1 +  )n
)n
Substituting the values, we have
13230 = 12000 (1 + 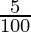 )T
)T
13230 = 12000 (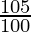 )T
)T
(21/20)T = 13230/12000
(21/20)T = 441/400
(21/20)T = (21/20)2
So on comparing both the sides, n = T = 2
Therefore,
Time required is 2 years.
Question 22. At what rate percent per annum will a sum of Rs. 4000 yield compound interest of Rs. 410 in 2 years?
Solution:
We have,
Principal = Rs 4000
Time = 2 years
CI = Rs 410
Rate be = R% per annum
By using the formula,
CI = P [(1 +  )n – 1]
)n – 1]
Substituting the values, we have
410 = 4000 [(1 +  )2 – 1]
)2 – 1]
410 = 4000 (1 +  )2 – 4000
)2 – 4000
410 + 4000 = 4000 (1 +  )2
)2
(1 +  )2 = 4410/4000
)2 = 4410/4000
(1 +  )2 = 441/400
)2 = 441/400
(1 +  )2 = (21/20)2
)2 = (21/20)2
By canceling the powers on both the sides,
1 +  = 21/20
= 21/20
 = 21/20 – 1
= 21/20 – 1
= (21-20)/20
= 1/20
R = 100/20
= 5
Therefore,
Required Rate is 5% per annum.
Question 23. A sum of money deposited at 2% per annum compounded annually becomes Rs. 10404 at the end of 2 years. Find the sum deposited.
Solution:
We have,
Time = 2years
Amount = Rs 10404
Rate be = 2% per annum
Let principal be = Rs P
By using the formula,
A = P [(1 +  )n
)n
Substituting the values, we have
10404 = P [(1 + 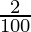 )2]
)2]
10404 = P [1.0404]
P = 10404/1.0404
= 10000
Therefore,
Required sum is Rs 10000.
Question 24. In how much time will a sum of Rs. 1600 amount to Rs. 1852.20 at 5% per annum compound interest?
Solution:
We have,
Principal = Rs 1600
Amount = Rs 1852.20
Rate = 5% per annum
Let time = T years
By using the formula,
A = P (1 +  )n
)n
Substituting the values, we have
1852.20 = 1600 (1 + 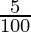 )T
)T
1852.20 = 1600 (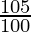 )T
)T
(21/20)T = 1852.20/1600
(21/20)T = 9261/8000
(21/20)T = (21/20)3
So on comparing both the sides, n = T = 3
Therefore,
Time required is 3 years.
Question 25. At what rate percent will a sum of Rs. 1000 amount to Rs. 1102.50 in 2 years at compound interest?
Solution:
We have,
Principal = Rs 1000
Amount = Rs 1102.50
Rate = R% per annum
Let time = 2 years
By using the formula,
A = P (1 +  )n
)n
Substituting the values, we have
1102.50 = 1000 (1 +  )2
)2
(1 +  )2 = 1102.50/1000
)2 = 1102.50/1000
(1 +  )2 = 4410/4000
)2 = 4410/4000
(1 + )2 = (21/20)2
)2 = (21/20)2
1 +  = 21/20
= 21/20
 = 21/20 – 1
= 21/20 – 1
= (21-20)/20
= 1/20
R = 100/20
= 5
Therefore,
Required Rate is 5%.
Question 26. The compound interest on Rs. 1800 at 10% per annum for a certain period of time is Rs. 378. Find the time in years.
Solution:
We have,
Principal = Rs 1800
CI = Rs 378
Rate = 10% per annum
Let time = T years
By using the formula,
CI = P [(1 +  )n – 1]
)n – 1]
Substituting the values, we have
378 = 1800 [(1 + 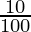 )T – 1]
)T – 1]
378 = 1800 [(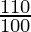 )T – 1]
)T – 1]
378 = 1800 [(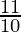 )T – 1800
)T – 1800
378 + 1800 = 1800 [(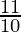 )T
)T
(11/10)T = 2178/1800
(11/10)T = 726/600
(11/10)T = 121/100
(11/10)T = (11/10)2
So on comparing both the sides, n = T = 2
Therefore,
Time required is 2 years.
Question 27. What sum of money will amount to Rs. 45582.25 at 6 ¾ % per annum in two years, interest being compounded annually
Solution:
We have,
Time = 2years
Amount = Rs 45582.25
Rate be = 6 ¾ % per annum = 27/4%
Let principal be = Rs P
By using the formula,
A = P [(1 +  )n
)n
Substituting the values, we have
45582.25 = P [(1 + 27/4×100)2]
45582.25 = P (1 + 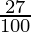 )2
)2
45582.25 = P (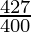 )2
)2
45582.25 = P × 427/400 × 427/400
P = (45582.25 × 400 × 400) / (427×427)
P = 7293160000/182329
= 40000
Therefore,
Required sum is Rs 40000.
Question 28. Sum of money amounts to Rs. 453690 in 2 years at 6.5% per annum compounded annually. Find the sum.
Solution:
We have,
Time = 2years
Amount = Rs 453690
Rate be = 6.5 % per annum
Let principal be = Rs P
By using the formula,
A = P [(1 +  )n
)n
Substituting the values, we have
453690 = P [(1 + 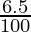 )2]
)2]
453690 = P (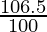 )2
)2
453690 = P × 106.5/100 × 106.5/100
P = (453690 × 100 × 100) / (106.5×106.5)
P = 4536900000/11342.25
= 400000
Therefore,
Required sum is Rs 400000.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...