Check whether given circle resides in boundary maintained by two other circles

Given outer circle radius R and inner circle radius r, making circles from the same center and forming the boundary between them. Now, given X and  Y coordinates which denote the center of the new circle to be formed with radius rad, your task is to check whether the circle with coordinates X and Y as the center can fit in the boundary of circles formed or not.
Examples: 

Input: R = 8, r = 4, x = 5, y = 3, rad = 1
Output: Fits

Input: R =9, r = 4, x = 5, y = 3, rad = 1
Output: Fits

Input :  R = 8, r = 4, x = 5, y = 3,  rad = 3.
Output: Doesn’t Fit

Approach: The idea is to calculate the distance between the center (0, 0) and the coordinates of the circle to be checked. 

• If 
  • distance + radius (of the circle to be checked) is less than or equal to Outer Radius and 
  • distance – radius (of the circle to be checked) is greater than or equal to Radius Inner circle, 
• It will fit

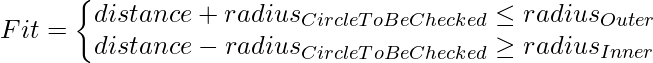
Below is the implementation of the above approach:

C++

// CPP program to check whether circle with given
// co-ordinates reside within the boundary
// of outer circle and inner circle
#include <bits/stdc++.h>
using namespace std;

// function to check if given circle fit in
// boundary or not
void fitOrNotFit(int R, int r, int x, int y,
                                 int rad) {

    // Distance from the center
    double val = sqrt(pow(x, 2) + pow(y, 2));

    // Checking the corners of circle
    if (val + rad <= R && val - rad >= r)
        cout << "Fits\n";
    else
        cout << "Doesn't Fit\n";
}

// driver program
int main()
{
    // Radius of outer circle and inner circle
    // respectively
    int R = 8, r = 4;

    // Co-ordinates and radius of the circle
    // to be checked
    int x = 5, y = 3, rad = 3;
    fitOrNotFit(R, r, x, y, rad);
    return 0;
}

Java

// Java program to check whether circle with given
// co-ordinates reside within the boundary
// of outer circle and inner circle
import java.util.*;

class GFG
{
// function to check if given circle fit in
// boundary or not
static void fitOrNotFit(int R, int r, int x, int y,
                                        int rad)
{
    // Distance from the center
    double val = Math.sqrt(Math.pow(x, 2) +
                           Math.pow(y, 2));

    // Checking the corners of circle
    if (val + rad <= R && val - rad >= r)
        System.out.println("Fits");
    else
    System.out.println("Doesn't Fit");
}

// driver program
public static void main (String[] args)
{
    // Radius of outer circle and inner circle
    // respectively
    int R = 8, r = 4;

    // Co-ordinates and radius of the circle
    // to be checked
    int x = 5, y = 3, rad = 3;
    fitOrNotFit(R, r, x, y, rad);
}
}
/* This Code is contributed by Kriti Shukla */

Python3

# Python3 program to check
# whether circle with given
# co-ordinates reside
# within the boundary
# of outer circle
# and inner circle

import math

# function to check if
# given circle fit in
# boundary or not
def fitOrNotFit(R, r, x, y, rad) :

    # Distance from the center
    val = math.sqrt(math.pow(x, 2) + math.pow(y, 2))

    # Checking the corners of circle
    if (val + rad <= R and val - rad >= r) :
        print("Fits\n")
    else:
        print("Doesn't Fit")


# driver program

# Radius of outer circle and inner circle
# respectively
R = 8
r = 4

# Co-ordinates and radius of the circle
# to be checked
x = 5
y = 3
rad = 3

fitOrNotFit(R, r, x, y, rad)

# This code is contributed by
# Smitha Dinesh Semwal

C#

// C# program to check whether circle with given
// co-ordinates reside within the boundary
// of outer circle and inner circle
using System;

class GFG
{
    // function to check if given circle fit in
    // boundary or not
    static void fitOrNotFit(int R, int r, int x, int y,
                                            int rad)
    {
        // Distance from the center
        double val = Math.Sqrt(Math.Pow(x, 2) +
                               Math.Pow(y, 2));

        // Checking the corners of circle
        if (val + rad <= R && val - rad >= r)
            Console.WriteLine("Fits");
        else
        Console.WriteLine("Doesn't Fit");
    }

    // Driver program
    public static void Main ()
    {
        // Radius of outer circle and inner circle
        // respectively
        int R = 8, r = 4;

        // Co-ordinates and radius of the circle
        // to be checked
        int x = 5, y = 3, rad = 3;
        fitOrNotFit(R, r, x, y, rad);
    }
}

// This Code is contributed by Anant Agarwal.

PHP

<?php
// PHP program to check whether
// circle with given co-ordinates
// reside within the boundary
// of outer circle and inner circle

// function to check if given
// circle fit in boundary or not
function fitOrNotFit($R, $r, $x, $y,
                               $rad)
{

    // Distance from the center
    $val = sqrt(pow($x, 2) + pow($y, 2));

    // Checking the corners of circle
    if ($val + $rad <= $R && $val -
                  $rad >= $r)
        echo"Fits\n";
    else
        echo "Doesn't Fit\n";
}

    // Driver Code

    // Radius of outer circle and
    // inner circle respectively
    $R = 8; $r = 4;

    // Co-ordinates and radius of
    // the circle to be checked
    $x = 5; $y = 3; $rad = 3;
    fitOrNotFit($R, $r, $x, $y, $rad);

// This Code is contributed by vt_m.
?>

Javascript

<script>

// Javascript program to check whether circle with given
// co-ordinates reside within the boundary
// of outer circle and inner circle

// function to check if given circle fit in
// boundary or not
function fitOrNotFit(R, r, x, y, rad) {

    // Distance from the center
    var val = Math.sqrt(Math.pow(x, 2) + Math.pow(y, 2));

    // Checking the corners of circle
    if (val + rad <= R && val - rad >= r)
        document.write( "Fits<br>");
    else
        document.write( "Doesn't Fit<br>");
}

// driver program
// Radius of outer circle and inner circle
// respectively
var R = 8, r = 4;

// Co-ordinates and radius of the circle
// to be checked
var x = 5, y = 3, rad = 3;
fitOrNotFit(R, r, x, y, rad);


</script>

Output

Doesn't Fit

Time Complexity: O(log n) since using inbuilt sqrt and pow function
Auxiliary Space: O(1)

This article is contributed by Aarti_Rathi and Rohit Thapliyal. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.