Check if a number can be expressed as a sum of consecutive numbers
Last Updated :
30 Sep, 2023
Given a number n, the task is to check whether it can be expressed as a sum of two or more consecutive numbers or not.
Example
Input : n = 10
Output : true
It can be expressed as sum of two consecutive
numbers 1 + 2 + 3 + 4.
Input : n = 16
Output : false
It cannot be expressed as sum of two consecutive
numbers.
Input : n = 5
Output : true
2 + 3 = 5
There is a direct and quick method to solve this. If a number is a power of two, then it cannot be expressed as a sum of consecutive numbers otherwise Yes.
The idea is based on below two facts.
1) Sum of any two consecutive numbers is odd as one of them has to be even and the other odd.
2) 2n = 2n-1 + 2n-1
If we take a closer look at 1) and 2), we can get the intuition behind the fact.
Below is the implementation of the above idea.
C++
#include<bits/stdc++.h>
using namespace std;
bool canBeSumofConsec(unsigned int n)
{
return ((n&(n-1)) && n);
}
int main()
{
unsigned int n = 15;
canBeSumofConsec(n)? cout << "true" :
cout << "false";
return 0;
}
|
Java
class Test
{
static boolean canBeSumofConsec(int n)
{
return (((n&(n-1))!=0) && n!=0);
}
public static void main(String[] args)
{
int n = 15;
System.out.println(canBeSumofConsec(n) ? "true" : "false");
}
}
|
Python3
def canBeSumofConsec(n) :
return ((n&(n-1)) and n)
n = 15
if(canBeSumofConsec(n)) :
print("true")
else :
print("false")
|
C#
using System;
class Test
{
static bool canBeSumofConsec(int n)
{
return (((n & (n - 1)) != 0) && n != 0);
}
public static void Main()
{
int n = 15;
Console.Write(canBeSumofConsec(n) ? "True" : "False");
}
}
|
Javascript
<script>
function canBeSumofConsec(n)
{
return (((n&(n-1))!=0) && n!=0);
}
let n = 15;
document.write(canBeSumofConsec(n) ? "true" : "false");
</script>
|
PHP
<?php
function canBeSumofConsec($n)
{
return (($n & ($n - 1)) && $n);
}
$n = 15;
if(canBeSumofConsec($n))
echo "true" ;
else
echo "false";
?>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Another Approach :
Let number chosen to represent N as a sum of consecutive numbers be X + 1, X + 2, X + 3 …. Y
Sum of these chosen numbers = Sum of first Y natural numbers – Sum of first X natural number
Sum of first Y natural number = 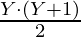 Sum of first X natural number =
Sum of first X natural number = 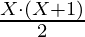 We know that, N = Sum of first Y natural number – Sum of first X natural number
We know that, N = Sum of first Y natural number – Sum of first X natural number 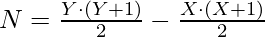 [Tex]2N = Y \cdot (Y + 1) – X \cdot (X + 1)
[/Tex]
[Tex]2N = Y \cdot (Y + 1) – X \cdot (X + 1)
[/Tex]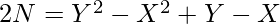 [Tex]2N = (Y – X) \cdot (Y + X + 1)
[/Tex]Let Y – X = a, Y + X + 1 = b Y + X + 1 > Y – X, b > a
[Tex]2N = (Y – X) \cdot (Y + X + 1)
[/Tex]Let Y – X = a, Y + X + 1 = b Y + X + 1 > Y – X, b > a 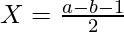 ,
, 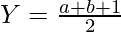 2N = a * b It means that a and b are factor of 2N, we know that X and Y are integers so, 1. b – a – 1 => multiple of 2 (Even number) 2. b + a + 1 => multiple of 2 (Even number)
2N = a * b It means that a and b are factor of 2N, we know that X and Y are integers so, 1. b – a – 1 => multiple of 2 (Even number) 2. b + a + 1 => multiple of 2 (Even number)
Both conditions must be satisfied
From 1 and 2 we can say that either one of them (a, b) should be Odd and another one Even
So if the number (2N) has only odd factors (can’t be possible as it is an even number (2N not N) ) or only even factors we can’t represent it as a sum of any consecutive natural numbers
So now, we have to now only check whether it has an odd factor or not
1. If the number (2N not N) does not have any odd factor (contains only even factor means can be represented as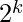 ) then we can’t represent it as a sum of consecutive number
) then we can’t represent it as a sum of consecutive number
2. If the number (2N not N) has an odd factor then we can represent it as a sum of a consecutive number
After this we have to only check whether we can represent (2N as 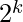 ) or not
) or not
- if Yes then answer is false or 0
- if No then answer is true or 1
Below is the implementation of the above idea :
C++14
#include <bits/stdc++.h>
using namespace std;
long long int canBeSumofConsec(long long int n)
{
n = 2 * n;
return ((n & (n - 1)) != 0);
}
int main()
{
long long int n = 10;
cout<<canBeSumofConsec(n)<<"\n";
}
|
C
#include <stdio.h>
long long int canBeSumofConsec(long long int n)
{
n = 2 * n;
return ((n & (n - 1)) != 0);
}
int main()
{
long long int n = 10;
printf("%lld", canBeSumofConsec(n));
}
|
Java
import java.util.*;
class GFG{
static int canBeSumofConsec( int n)
{
n = 2 * n;
return ((n & (n - 1)) != 0)?1:0;
}
public static void main(String[] args)
{
int n = 10;
System.out.print(canBeSumofConsec(n)+"\n");
}
}
|
Python3
def canBeSumofConsec(n):
n = 2 * n;
if((n & (n - 1)) != 0):
return 1;
else:
return 0;
if __name__ == '__main__':
n = 10;
print(canBeSumofConsec(n));
|
C#
using System;
public class GFG {
static int canBeSumofConsec(int n)
{
n = 2 * n;
return ((n & (n - 1)) != 0) ? 1 : 0;
}
public static void Main(String[] args) {
int n = 10;
Console.Write(canBeSumofConsec(n) + "\n");
}
}
|
Javascript
<script>
function canBeSumofConsec(n) {
n = 2 * n;
return ((n & (n - 1)) != 0) ? 1 : 0;
}
var n = 10;
document.write(canBeSumofConsec(n) + "\n");
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Approach#3:Using Brute Force
Start a loop from 1 to n/2 (inclusive) For each value i in the loop, start another loop from i+1 to n/2+1 (inclusive) Calculate the sum of consecutive numbers from i to j If the sum is equal to n, return True If the sum is greater than n, break the inner loop and start the next iteration of the outer loop If no consecutive sum is found, return False
Algorithm
1. Define a function is_sum_of_consecutive_numbers(n)
2. Start a loop from 1 to n/2 (inclusive)
3. For each value i in the loop, start another loop from i+1 to n/2+1 (inclusive)
4. Calculate the sum of consecutive numbers from i to j
5. If the sum is equal to n, return True
6. If the sum is greater than n, break the inner loop and start the next iteration of the outer loop
7. If no consecutive sum is found, return False
C++
#include <iostream>
bool is_sum_of_consecutive_numbers(int n) {
for (int i = 1; i < (n / 2 + 2); i++) {
for (int j = i + 1; j < (n / 2 + 2); j++) {
int sum_consecutive = (j - i + 1) * (i + j) / 2;
if (sum_consecutive == n) {
return true;
}
else if (sum_consecutive > n) {
break;
}
}
}
return false;
}
int main() {
int n = 10;
std::cout << std::boolalpha << is_sum_of_consecutive_numbers(n) << std::endl;
return 0;
}
|
Java
public class Main {
public static boolean isSumOfConsecutiveNumbers(int n) {
for (int i = 1; i < (n / 2 + 2); i++) {
for (int j = i + 1; j < (n / 2 + 2); j++) {
int sumConsecutive = (j - i + 1) * (i + j) / 2;
if (sumConsecutive == n) {
return true;
} else if (sumConsecutive > n) {
break;
}
}
}
return false;
}
public static void main(String[] args) {
int n = 10;
System.out.println(isSumOfConsecutiveNumbers(n));
}
}
|
Python3
def is_sum_of_consecutive_numbers(n):
for i in range(1, n//2+2):
for j in range(i+1, n//2+2):
sum_consecutive = (j-i+1)*(i+j)//2
if sum_consecutive == n:
return True
elif sum_consecutive > n:
break
return False
n=10
print(is_sum_of_consecutive_numbers(n))
|
C#
using System;
class GFG
{
static bool IsSumOfConsecutiveNumbers(int n)
{
for (int i = 1; i < (n / 2 + 2); i++)
{
for (int j = i + 1; j < (n / 2 + 2); j++)
{
int sumConsecutive = (j - i + 1) * (i + j) / 2;
if (sumConsecutive == n)
{
return true;
}
else if (sumConsecutive > n)
{
break;
}
}
}
return false;
}
static void Main(string[] args)
{
int n = 10;
Console.WriteLine($"{IsSumOfConsecutiveNumbers(n)}");
}
}
|
Javascript
function is_sum_of_consecutive_numbers(n) {
for (let i = 1; i < (n / 2 + 2); i++) {
for (let j = i + 1; j < (n / 2 + 2); j++) {
let sum_consecutive = (j - i + 1) * (i + j) / 2;
if (sum_consecutive == n) {
return true;
}
else if (sum_consecutive > n) {
break;
}
}
}
return false;
}
let n = 10;
console.log(is_sum_of_consecutive_numbers(n));
|
Time complexity: O(n^2)
Space complexity: O(1)
Reference:
http://www.cut-the-knot.org/arithmetic/UnpropertyOfPowersOf2.shtml
Share your thoughts in the comments
Please Login to comment...