How to check if an instance of 15 puzzle is solvable?
Last Updated :
17 Mar, 2023
Given a 4×4 board with 15 tiles (every tile has one number from 1 to 15) and one empty space. The objective is to place the numbers on tiles in order using the empty space. We can slide four adjacent (left, right, above and below) tiles into the empty space. For example,
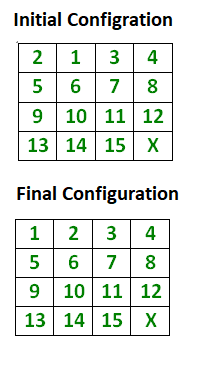
Here X marks the spot to where the elements can be shifted and the final configuration always remains the same the puzzle is solvable.
In general, for a given grid of width N, we can find out check if a N*N – 1 puzzle is solvable or not by following below simple rules :
- If N is odd, then puzzle instance is solvable if number of inversions is even in the input state.
- If N is even, puzzle instance is solvable if
- the blank is on an even row counting from the bottom (second-last, fourth-last, etc.) and number of inversions is odd.
- the blank is on an odd row counting from the bottom (last, third-last, fifth-last, etc.) and number of inversions is even.
- For all other cases, the puzzle instance is not solvable.
What is an inversion here?
If we assume the tiles written out in a single row (1D Array) instead of being spread in N-rows (2D Array), a pair of tiles (a, b) form an inversion if a appears before b but a > b.
For above example, consider the tiles written out in a row, like this:
2 1 3 4 5 6 7 8 9 10 11 12 13 14 15 X
The above grid forms only 1 inversion i.e. (2, 1).
Illustration:

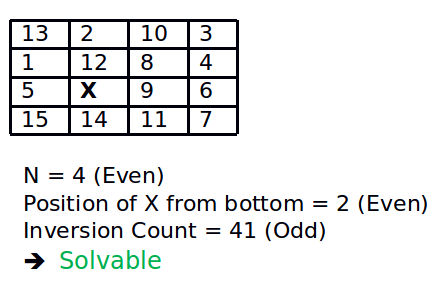
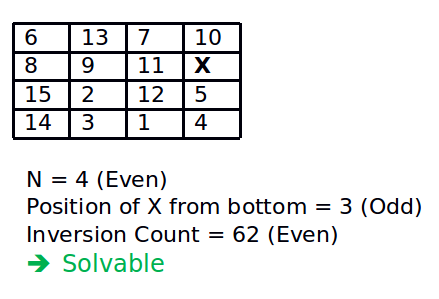
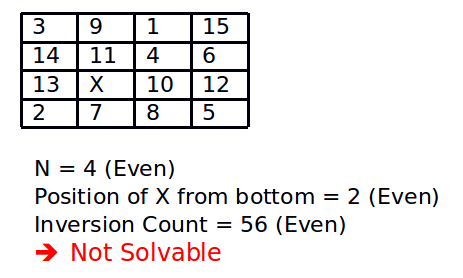
Below is a simple C++ program to check whether a given instance of 15 puzzle is solvable or not. The program is generic and can be extended to any grid width.
C++
#include <iostream>
#define N 4
using namespace std;
int getInvCount(int arr[])
{
int inv_count = 0;
for (int i = 0; i < N * N - 1; i++)
{
for (int j = i + 1; j < N * N; j++)
{
if (arr[j] && arr[i] && arr[i] > arr[j])
inv_count++;
}
}
return inv_count;
}
int findXPosition(int puzzle[N][N])
{
for (int i = N - 1; i >= 0; i--)
for (int j = N - 1; j >= 0; j--)
if (puzzle[i][j] == 0)
return N - i;
}
bool isSolvable(int puzzle[N][N])
{
int invCount = getInvCount((int*)puzzle);
if (N & 1)
return !(invCount & 1);
else
{
int pos = findXPosition(puzzle);
if (pos & 1)
return !(invCount & 1);
else
return invCount & 1;
}
}
int main()
{
int puzzle[N][N] =
{
{12, 1, 10, 2},
{7, 11, 4, 14},
{5, 0, 9, 15},
{8, 13, 6, 3},
};
isSolvable(puzzle)? cout << "Solvable":
cout << "Not Solvable";
return 0;
}
|
Java
import java.util.*;
class Main {
static final int N = 4;
static int getInvCount(int[] arr)
{
int inv_count = 0;
for (int i = 0; i < N * N - 1; i++) {
for (int j = i + 1; j < N * N; j++) {
if (arr[j] != 0 && arr[i] != 0
&& arr[i] > arr[j])
inv_count++;
}
}
return inv_count;
}
static int findXPosition(int[][] puzzle)
{
for (int i = N - 1; i >= 0; i--)
for (int j = N - 1; j >= 0; j--)
if (puzzle[i][j] == 0)
return N - i;
return -1;
}
static boolean isSolvable(int[][] puzzle)
{
int[] arr = new int[N * N];
int k = 0;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
arr[k++] = puzzle[i][j];
int invCount = getInvCount(arr);
if (N % 2 == 1)
return invCount % 2 == 0;
else
{
int pos = findXPosition(puzzle);
if (pos % 2 == 1)
return invCount % 2 == 0;
else
return invCount % 2 == 1;
}
}
public static void main(String[] args)
{
int[][] puzzle
= { { 12, 1, 10, 2 },
{ 7, 11, 4, 14 },
{ 5, 0, 9,
15 },
{ 8, 13, 6, 3 } };
System.out.println(isSolvable(puzzle)
? "Solvable"
: "Not Solvable");
}
}
|
PHP
<?php
$N= 4;
function getInvCount( $arr)
{
global $N;
$inv_count = 0;
for ($i = 0; $i < $N * $N - 1; $i++)
{
for ($j = $i + 1; $j < $N * $N; $j++)
{
$inv_count++;
}
}
return $inv_count;
}
function findXPosition($puzzle)
{
global $N;
for ($i = $N - 1; $i >= 0; $i--)
for ($j = $N - 1; $j >= 0; $j--)
if ($puzzle[$i][$j] == 0)
return $N - $i;
}
function isSolvable( $puzzle)
{
global $N;
$invCount = getInvCount($puzzle);
if ($N & 1)
return !($invCount & 1);
else
{
$pos = findXPosition($puzzle);
if ($pos & 1)
return !($invCount & 1);
else
return $invCount & 1;
}
}
$puzzle =
array(
array(12, 1, 10, 2),
array(7, 11, 4, 14),
array(5, 0, 9, 15),
array(8, 13, 6, 3),
);
if(isSolvable($puzzle)==0)
echo "Solvable";
else
echo "Not Solvable";
#This code is contributed by aj_36
?>
|
Python3
N=4
def getInvCount(arr):
arr1=[]
for y in arr:
for x in y:
arr1.append(x)
arr=arr1
inv_count = 0
for i in range(N * N - 1):
for j in range(i + 1,N * N):
if (arr[j] and arr[i] and arr[i] > arr[j]):
inv_count+=1
return inv_count
def findXPosition(puzzle):
for i in range(N - 1,-1,-1):
for j in range(N - 1,-1,-1):
if (puzzle[i][j] == 0):
return N - i
def isSolvable(puzzle):
invCount = getInvCount(puzzle)
if (N & 1):
return ~(invCount & 1)
else:
pos = findXPosition(puzzle)
if (pos & 1):
return ~(invCount & 1)
else:
return invCount & 1
if __name__ == '__main__':
puzzle =[
[12, 1, 10, 2,],
[7, 11, 4, 14,],
[5, 0, 9, 15,],
[8, 13, 6, 3,],]
print("Solvable") if isSolvable(puzzle) else print("Not Solvable")
|
C#
using System;
class Program {
const int N = 4;
static int getInvCount(int[] arr)
{
int inv_count = 0;
for (int i = 0; i < N * N - 1; i++) {
for (int j = i + 1; j < N * N; j++) {
if (arr[j] != 0 && arr[i] != 0
&& arr[i] > arr[j])
inv_count++;
}
}
return inv_count;
}
static int findXPosition(int[, ] puzzle)
{
for (int i = N - 1; i >= 0; i--) {
for (int j = N - 1; j >= 0; j--) {
if (puzzle[i, j] == 0)
return N - i;
}
}
return -1;
}
static bool isSolvable(int[, ] puzzle)
{
int[] arr = new int[N * N];
int k = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
arr[k++] = puzzle[i, j];
}
}
int invCount = getInvCount(arr);
if (N % 2 == 1)
return invCount % 2 == 0;
else
{
int pos = findXPosition(puzzle);
if (pos % 2 == 1)
return invCount % 2 == 0;
else
return invCount % 2 == 1;
}
}
static void Main(string[] args)
{
int[, ] puzzle = new int[N, N] {
{ 12, 1, 10, 2 },
{ 7, 11, 4, 14 },
{ 5, 0, 9, 15 },
{ 8, 13, 6,
3 }
};
if (isSolvable(puzzle))
Console.WriteLine("Solvable");
else
Console.WriteLine("Not Solvable");
}
}
|
Javascript
const N = 4;
function getInvCount(arr) {
let inv_count = 0;
for (let i = 0; i < N * N - 1; i++)
{
for (let j = i + 1; j < N * N; j++)
{
if (arr[j] && arr[i] && arr[i] > arr[j])
inv_count++;
}
}
return inv_count;
}
function findXPosition(puzzle)
{
for (let i = N - 1; i >= 0; i--)
for (let j = N - 1; j >= 0; j--)
if (puzzle[i][j] == 0)
return N - i;
}
function isSolvable(puzzle)
{
let invCount = getInvCount(puzzle);
if (N & 1)
return !(invCount & 1);
else {
let pos = findXPosition(puzzle);
if (pos & 1)
return !(invCount & 1);
else
return invCount & 1;
}
}
function main() {
let puzzle = [
[12, 1, 10, 2],
[7, 11, 4, 14],
[5, 0, 9, 15],
[8, 13, 6, 3],
];
(isSolvable(puzzle)) ? console.log("Solvable") :
console.log("Not Solvable");
return 0;
}
main();
|
Time Complexity : O(n2)
Space Complexity: O(n)
How does this works?
Fact 1: For a grid of odd width, all legal moves preserve the polarity (even or odd) of the number of inversions.
Proof of Fact 1
- Moving a tile along the row (left or right) doesn’t change the number of inversions, and therefore doesn’t change its polarity.
- Moving a tile along the column (up or down) can change the number of inversions. The tile moves past an even number of other tiles (N – 1). So move either increases/decreases inversion count by 2, or keeps the inversion count same.
Fact 2: For a grid of even width, the following is invariant: (#inversions even) == (blank on odd row from bottom).
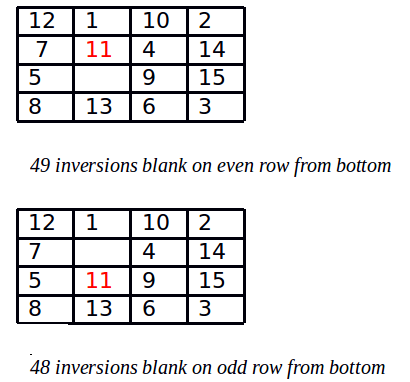
Example: Consider the move above. The number of inversions on the left is 49, and the blank is on an even row from the bottom. So the value of the invariant is “false == false”, which is true. The number of inversions on the right is 48, because the 11 has lost two inversions, but the 14 has gained one. The blank is on an odd row from the bottom. So the value of the invariant is “true==true”, which is still true.
Proof of Fact 2
- Moving a tile along the row (left or right) doesn’t change the number of inversions and doesn’t change the row of the blank.
- Moving a tile along the column (up or down) does change the number of inversions. The tile moves past an odd number of other tiles (N – 1). So the number of inversions changes by odd number of times. The row of the blank also changes, from odd to even, or from even to odd. So both halves of the invariant changes. So its value is preserved.
Combining Fact 1 + Fact 2 = Fact 3:
- If the width is odd, then every solvable state has an even number of inversions.
If the width is even, then every solvable state has
- an even number of inversions if the blank is on an odd numbered row counting from the bottom;
- an odd number of inversions if the blank is on an even numbered row counting from the bottom;
Proof of fact 3:
- The initial (solved) state has those properties.
- Those properties are preserved by every legal move.
- Any solvable state can be reached from the initial state by some sequence of legal moves.
Related Article:
How to check if an instance of 8 puzzle is solvable?
Source :
https://www.cs.bham.ac.uk/~mdr/teaching/modules04/java2/TilesSolvability.html
Share your thoughts in the comments
Please Login to comment...