Check whether jigsaw puzzle solvable or not
Last Updated :
27 Dec, 2022
Given a special Jigsaw puzzle consisting of N rows and M columns all identical pieces. Every piece has three tabs and one blank. The task is to check if the puzzle is solvable by placing the pieces in such a way that the tab of one piece fits perfectly into a blank of other piece.

Note: Rotate and Translate the pieces to solve the puzzle.
Examples:
Input: N = 2, M = 2
Output: Yes

Input: N = 1, M = 3
Output: Yes
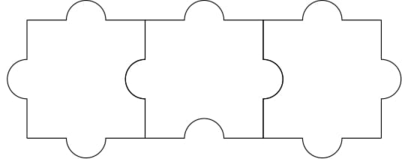
Approach: The key observation in the problem is that:
- If the Puzzle has only one row or only one column. Then it is possible to solve the puzzle by placing a blank tab on that shared side itself.
- If the Puzzle has two rows and two columns. Then The puzzle is solvable by placing the blank Tabs in a circular chain.
- Otherwise, It is not possible to solve the Puzzle.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void checkSolvable(int n, int m)
{
if (n == 1 or m == 1)
cout << "YES";
else if (m == 2 and n == 2)
cout << "YES";
else
cout << "NO";
}
int main()
{
int n = 1, m = 3;
checkSolvable(n, m);
}
|
Java
import java.util.*;
class GFG{
static void checkSolvable(int n, int m)
{
if (n == 1 || m == 1)
System.out.print("YES");
else if (m == 2 && n == 2)
System.out.print("YES");
else
System.out.print("NO");
}
public static void main(String[] args)
{
int n = 1, m = 3;
checkSolvable(n, m);
}
}
|
Python
def checkSolvable(n, m):
if n == 1 or m == 1:
print("YES")
elif m == 2 and n == 2:
print("YES")
else:
print("NO")
if __name__ == "__main__":
n = 1
m = 3
checkSolvable(n, m)
|
C#
using System;
class GFG{
static void checkSolvable(int n, int m)
{
if (n == 1 || m == 1)
Console.WriteLine("YES");
else if (m == 2 && n == 2)
Console.WriteLine("YES");
else
Console.WriteLine("NO");
}
public static void Main()
{
int n = 1, m = 3;
checkSolvable(n, m);
}
}
|
Javascript
<script>
function checkSolvable(n, m)
{
if (n == 1 || m == 1)
document.write("YES");
else if (m == 2 && n == 2)
document.write("YES");
else
document.write("NO");
}
let n = 1, m = 3;
checkSolvable(n, m);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...