Check if array contains contiguous integers with duplicates allowed

Given an array Arr of N integers(duplicates allowed). Print “Yes” if it is a set of contiguous integers else print “No”.
Examples: 

Input: Arr = { 5, 2, 3, 6, 4, 4, 6, 6 } 
Output: Yes 
The elements of array form a contiguous set of integers which is {2, 3, 4, 5, 6} so the output is Yes.
Input: Arr = { 10, 14, 10, 12, 12, 13, 15 } 
Output: No

Approach: 

1. A similar approach is discussed here. It is recommended to go through it before moving further with this article.
2. Find the max and min elements from the array.
3. Update the array with the difference from the max element in the array.
4. Traverse the array and do the following 
   • If 0 <= abs(arr[i])-1) < n and arr[abs(arr[i])-1)] > 0 means the element is positive (visited first time), make it negative by doing arr[abs(arr[i])-1] = -arr[abs(arr[i])-1].
   • Else continue loop means either the value is already visited or out of range of the array
5. Traverse the loop again and check if any element is positive means element has a difference greater than 1 
   break the loop and print “NO”
6. If no element is found positive, print “YES”

Below is the implementation code: 

C++

// C++ program to check if
// array contains contiguous
// integers with duplicates
// allowed in O(1) space
#include <bits/stdc++.h>
using namespace std;

// Function to return true or
// false
bool check(int arr[], int n)
{

    int k = INT_MIN;
    int r = INT_MAX;

    // To find the max and min
    // in the array
    for (int i = 0; i < n; i++) {
        k = max(k, arr[i]);
        r = min(r, arr[i]);
    }

    k += 1;

    // Update the array with
    // the difference from
    // the max element
    for (int i = 0; i < n; i++)
        arr[i] = k - arr[i];

    for (int i = 0; i < n; i++) {

        // if the element is positive
        // and less than the size of
        // array(in range), make it negative
        if (abs(arr[i]) - 1 < n
            && arr[abs(arr[i]) - 1] > 0) {
            arr[abs(arr[i]) - 1]
                = -arr[abs(arr[i]) - 1];
        }
    }

    int flag = 0;

    // Loop from 0 to end of the array
    for (int i = 0; i <= k - r - 1; i++) {

        // Found positive, out of range
        if (arr[i] > 0) {
            flag = 1;
            break;
        }
    }

    return flag == 0;
}

// Driver function
int main()
{

    // Given array
    int arr[] = { 5, 2, 3, 6, 4, 4, 6, 6 };
    int n = sizeof(arr) / sizeof(arr[0]);

    // Function Calling
    if (check(arr, n))
        cout << "Yes";
    else
        cout << "No";

    return 0;
}

Java

// Java program to check if array contains
// contiguous integers with duplicates
// allowed in O(1) space
import java.util.*;

class GFG
{

// Function to return true or
// false
static boolean check(int arr[], int n)
{

    int k = Integer.MIN_VALUE;
    int r = Integer.MAX_VALUE;

    // To find the max and min
    // in the array
    for (int i = 0; i < n; i++)
    {
        k = Math.max(k, arr[i]);
        r = Math.min(r, arr[i]);
    }

    k += 1;

    // Update the array with
    // the difference from
    // the max element
    for (int i = 0; i < n; i++)
        arr[i] = k - arr[i];

    for (int i = 0; i < n; i++)
    {

        // if the element is positive
        // and less than the size of
        // array(in range), make it negative
        int abs_value = Math.abs(arr[i]);
        if (abs_value - 1 < n &&
        arr[abs_value - 1] > 0)
        {
            arr[abs_value - 1] = -arr[abs_value - 1];
        }
    }

    int flag = 0;

    // Loop from 0 to end of the array
    for (int i = 0; i <= k - r - 1; i++)
    {

        // Found positive, out of range
        if (arr[i] > 0)
        {
            flag = 1;
            break;
        }
    }
    return flag == 0;
}

// Driver function
public static void main(String []args)
{

    // Given array
    int arr[] = { 5, 2, 3, 6, 4, 4, 6, 6 };
    int n = arr.length;

    // Function Calling
    if (check(arr, n))
        System.out.println("Yes");
    else
        System.out.println("No");
}
}

// This code is contributed by Surendra_Gangwar

Python3

# Python3 program to check if array contains
# contiguous integers with duplicates allowed
# in O(1) space

# Function to return true or false
def check(arr, n):

    k = -10**9
    r = 10**9

    # To find the max and min in the array
    for i in range(n):
        k = max(k, arr[i])
        r = min(r, arr[i])

    k += 1

    # Update the array with the difference
    # from the max element
    for i in range(n):
        arr[i] = k - arr[i]

    for i in range(n):

        # if the element is positive
        # and less than the size of
        # array(in range), make it negative
        if (abs(arr[i]) - 1 < n and
                arr[abs(arr[i]) - 1] > 0):
            arr[abs(arr[i]) - 1]= -arr[abs(arr[i]) - 1]

    flag = 0

    # Loop from 0 to end of the array
    for i in range(k - r):

        # Found positive, out of range
        if (arr[i] > 0):
            flag = 1
            break

    return flag == 0

# Driver Code

# Given array
arr = [5, 2, 3, 6, 4, 4, 6, 6]
n = len(arr)

# Function Calling
if (check(arr, n)):
    print("Yes")
else:
    print("No")

# This code is contributed by Mohit Kumar

C#

// C# program to check if array contains
// contiguous integers with duplicates
// allowed in O(1) space
using System;

class GFG
{

// Function to return true or
// false
static bool check(int []arr, int n)
{
    int k = int.MinValue;
    int r = int.MaxValue;

    // To find the max and min
    // in the array
    for (int i = 0; i < n; i++)
    {
        k = Math.Max(k, arr[i]);
        r = Math.Min(r, arr[i]);
    }

    k += 1;

    // Update the array with
    // the difference from
    // the max element
    for (int i = 0; i < n; i++)
        arr[i] = k - arr[i];

    for (int i = 0; i < n; i++)
    {

        // if the element is positive
        // and less than the size of
        // array(in range), make it negative
        if (Math.Abs(arr[i]) - 1 < n &&
        arr[Math.Abs(arr[i]) - 1] > 0)
        {
            arr[Math.Abs(arr[i]) - 1] = -
                         arr[Math.Abs(arr[i]) - 1];
        }
    }

    int flag = 0;

    // Loop from 0 to end of the array
    for (int i = 0; i <= k - r - 1; i++)
    {

        // Found positive, out of range
        if (arr[i] > 0)
        {
            flag = 1;
            break;
        }
    }
    return flag == 0;
}

// Driver Code
static public void Main ()
{

    // Given array
    int []arr = { 5, 2, 3, 6, 4, 4, 6, 6 };
    int n = arr.Length;

    // Function Calling
    if (check(arr, n))
        Console.Write("Yes");
    else
        Console.Write("No");
}
}

// This code is contributed by ajit

Javascript

<script>

// Javascript program to check if
// array contains contiguous
// integers with duplicates
// allowed in O(1) space

// Function to return true or
// false
function check(arr, n)
{

    let k = Number.MIN_VALUE;
    let r = Number.MAX_VALUE;

    // To find the max and min
    // in the array
    for (let i = 0; i < n; i++) {
        k = Math.max(k, arr[i]);
        r = Math.min(r, arr[i]);
    }

    k += 1;

    // Update the array with
    // the difference from
    // the max element
    for (let i = 0; i < n; i++)
        arr[i] = k - arr[i];

    for (let i = 0; i < n; i++) {

        // if the element is positive
        // and less than the size of
        // array(in range), make it negative
        let abs_value = Math.abs(arr[i]);
        if (abs_value - 1 < n
            && arr[abs_value - 1] > 0) {
            arr[abs_value - 1]
                = -arr[abs_value - 1];
        }
    }

    let flag = 0;

    // Loop from 0 to end of the array
    for (let i = 0; i <= k - r - 1; i++) {

        // Found positive, out of range
        if (arr[i] > 0) {
            flag = 1;
            break;
        }
    }

    return flag == 0;
}

// Driver function

    // Given array
    let arr = [ 5, 2, 3, 6, 4, 4, 6, 6 ];
    let n = arr.length;

    // Function Calling
    if (check(arr, n))
        document.write("Yes");
    else
        document.write("No");

</script>

Output: 

Yes

Time Complexity: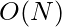 
Space Complexity: 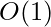Extra Space