Area of the circle that has a square and a circle inscribed in it
Last Updated :
05 Dec, 2022
Given the side of a square that is kept inside a circle. It keeps expanding until all four of its vertices touch the circumference of the circle. Another smaller circle is kept inside the square now and it keeps expanding until its circumference touches all four sides of the square. The outer and the inner circle form a ring. Find the area of this shaded part as shown in the image below.

Examples:
Input: a = 3
Output: 7.06858
Input: a = 4
Output: 12.566371
Approach:
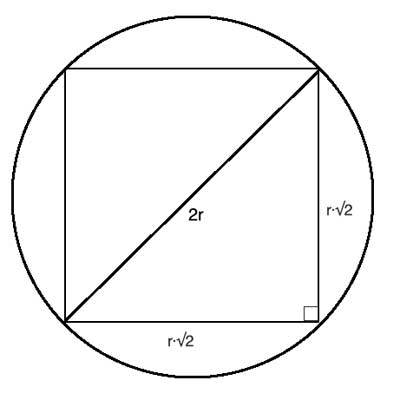
From the above figure, R = a / sqrt(2) can be derived where a is the side length of the square. The area of the outer circle is (pi * R * R).
Let s1 be the area of the outer circle (pi * R * R) and s2 be the area of the inner circle (pi * r * r). Then the area of the ring is s1 – s2.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float getArea(int a)
{
float area = (M_PI * a * a) / 4.0;
return area;
}
int main()
{
int a = 3;
cout << getArea(a);
return 0;
}
|
Java
public class GFG {
static float getArea(int a)
{
float area = (float)(Math.PI * a * a) / 4;
return area;
}
public static void main(String args[])
{
int a = 3;
System.out.println(getArea(a));
}
}
|
Python3
import math
def getArea(a):
area = (math.pi * a * a) / 4
return area
a = 3
print('{0:.6f}'.format(getArea(a)))
|
C#
using System;
class GFG
{
static float getArea(int a)
{
float area = (float)(Math.PI * a * a) / 4;
return area;
}
public static void Main()
{
int a = 3;
Console.Write(getArea(a));
}
}
|
Javascript
<script>
function getArea(a)
{
var area = (Math.PI * a * a) / 4;
return area;
}
var a = 3;
document.write(getArea(a));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...