Biggest Reuleaux Triangle inscribed within a Square inscribed in an equilateral triangle
Last Updated :
07 Aug, 2022
Given here is an equilateral triangle of sidelength a which inscribes a square which in turn inscribes a reuleaux triangle. The task is to find the maximum possible area of this reuleaux triangle.
Examples:
Input : a = 5
Output : 3.79335
Input : a = 9
Output : 12.2905

Approach: We know that the side of the square inscribed within an equilateral triangle of side length 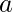 is, x = 0.464*a (Please refer here).
is, x = 0.464*a (Please refer here).
Also, in the reuleaux triangle, h = x.
So, Area of Reuleaux Triangle:
A = 0.70477*h2
= 0.70477*(0.464*a)2
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float Area(float a)
{
if (a < 0)
return -1;
float x = 0.464 * a;
float A = 0.70477 * pow(x, 2);
return A;
}
int main()
{
float a = 5;
cout << Area(a) << endl;
return 0;
}
|
Java
class GFG
{
static float Area(float a)
{
if (a < 0)
return -1;
float x = 0.464f * a;
float A = 0.70477f * (float)Math.pow(x, 2);
return A;
}
public static void main (String[] args)
{
float a = 5;
System.out.println(String.format("%.5f", Area(a)));
}
}
|
Python3
import math as mt
def Area(a):
if (a < 0):
return -1
x = 0.464 * a
A = 0.70477 * pow(x, 2)
return A
a = 5
print(Area(a))
|
C#
using System;
class GFG
{
static float Area(float a)
{
if (a < 0)
return -1;
float x = 0.464f * a;
float A = 0.70477f * (float)Math.Pow(x, 2);
return A;
}
public static void Main ()
{
float a = 5;
Console.WriteLine(String.Format("{0,0:#.00000}",
Area(a)));
}
}
|
PHP
<?php
function Area($a)
{
if ($a < 0)
return -1;
$x = 0.464 * $a;
$A = 0.70477 * pow($x, 2);
return $A;
}
$a = 5;
echo Area($a) . "\n";
|
Javascript
<script>
function Area( a)
{
if (a < 0)
return -1;
let x = 0.464 * a;
let A = 0.70477 * Math.pow(x, 2);
return A;
}
let a = 5;
document.write( Area(a).toFixed(5));
</script>
|
Time complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...