Analysis of Algorithms | Big – Θ (Big Theta) Notation
Last Updated :
02 Nov, 2023
In the analysis of algorithms, asymptotic notations are used to evaluate the performance of an algorithm, in its best cases and worst cases. This article will discuss Big – Theta notations represented by a Greek letter (Θ).
Definition: Let g and f be the function from the set of natural numbers to itself. The function f is said to be Θ(g), if there are constants c1, c2 > 0 and a natural number n0 such that c1* g(n) ≤ f(n) ≤ c2 * g(n) for all n ≥ n0
Mathematical Representation:
Θ (g(n)) = {f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1 * g(n) ≤ f(n) ≤ c2 * g(n) for all n ≥ n0}
Note: Θ(g) is a set
The above definition means, if f(n) is theta of g(n), then the value f(n) is always between c1 * g(n) and c2 * g(n) for large values of n (n ≥ n0). The definition of theta also requires that f(n) must be non-negative for values of n greater than n0.
Graphical Representation:

Graphical Representation
In simple language, Big – Theta(Θ) notation specifies asymptotic bounds (both upper and lower) for a function f(n) and provides the average time complexity of an algorithm.
Follow the steps below to find the average time complexity of any program:
- Break the program into smaller segments.
- Find all types and number of inputs and calculate the number of operations they take to be executed. Make sure that the input cases are equally distributed.
- Find the sum of all the calculated values and divide the sum by the total number of inputs let say the function of n obtained is g(n) after removing all the constants, then in Θ notation its represented as Θ(g(n))
Example: Consider an example to find whether a key exists in an array or not using linear search. The idea is to traverse the array and check every element if it is equal to the key or not.
The pseudo-code is as follows:
bool linearSearch(int a[], int n, int key)
{
for (int i = 0; i < n; i++) {
if (a[i] == key)
return true;
}
return false;
}
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool linearSearch(int a[], int n, int key)
{
for (int i = 0; i < n; i++) {
if (a[i] == key)
return true;
}
return false;
}
int main()
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int n = sizeof(arr) / sizeof(arr[0]);
if (linearSearch(arr, n, x))
cout << "Element is present in array";
else
cout << "Element is not present in array";
return 0;
}
|
Java
import java.lang.*;
import java.util.*;
class GFG{
static boolean linearSearch(int a[], int n,
int key)
{
for(int i = 0; i < n; i++)
{
if (a[i] == key)
return true;
}
return false;
}
public static void main(String[] args)
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int n = arr.length;
if (linearSearch(arr, n, x))
System.out.println("Element is present in array");
else
System.out.println("Element is not present in array");
}
}
|
Python3
def linearSearch(a, n, key):
for i in range(0, n):
if (a[i] == key):
return True
return False
arr = 2, 3, 4, 10, 40
x = 10
n = len(arr)
if (linearSearch(arr, n, x)):
print("Element is present in array")
else:
print("Element is not present in array")
|
C#
using System;
class GFG{
static bool linearSearch(int[] a, int n,
int key)
{
for(int i = 0; i < n; i++)
{
if (a[i] == key)
return true;
}
return false;
}
static void Main()
{
int[] arr = { 2, 3, 4, 10, 40 };
int x = 10;
int n = arr.Length;
if (linearSearch(arr, n, x))
Console.Write("Element is present in array");
else
Console.Write("Element is not present in array");
}
}
|
Javascript
<script>
function linearSearch(a, n, key)
{
for(var i = 0; i < n; i++)
{
if (a[i] == key)
return true;
}
return false;
}
var arr = [ 2, 3, 4, 10, 40 ];
var x = 10;
var n = arr.length;
if (linearSearch(arr, n, x))
document.write("Element is present in array");
else
document.write("Element is not present in array");
</script>
|
OutputElement is present in array
Time Complexity: O(n)
Auxiliary Space: O(1)
In a linear search problem, let’s assume that all the cases are uniformly distributed (including the case when the key is absent in the array). So, sum all the cases (when the key is present at position 1, 2, 3, ……, n and not present, and divide the sum by n + 1.
Average case time complexity = 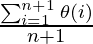
⇒ 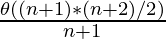
⇒ 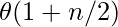
⇒ 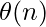 (constants are removed)
(constants are removed)
When to use Big – Θ notation: Big – Θ analyzes an algorithm with most precise accuracy since while calculating Big – Θ, a uniform distribution of different type and length of inputs are considered, it provides the average time complexity of an algorithm, which is most precise while analyzing, however in practice sometimes it becomes difficult to find the uniformly distributed set of inputs for an algorithm, in that case, Big-O notation is used which represent the asymptotic upper bound of a function f.
For more details, please refer: Design and Analysis of Algorithms.
Share your thoughts in the comments
Please Login to comment...